Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Circle: Tangents and Intersecting Chords
Revision Notes: Circle: Tangents and Intersecting Chords | Mathematics Class 10 ICSE PDF Download
Some terms associated with circle
- A line which intersects a circle at two distinct points is called a secant of the circle.
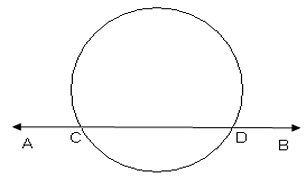 In the figure, AB is a secant to the circle.
In the figure, AB is a secant to the circle. - A tangent to a circle is a line that intersects the circle only at one point.
The common point of the circle and the tangent is called point of contact.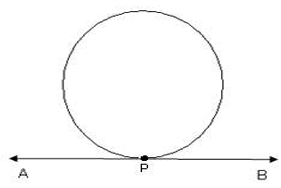 In the figure, AB is a tangent to the circle and P is the point of contact.
In the figure, AB is a tangent to the circle and P is the point of contact. - A tangent to a circle is a special case of the secant when the two end points of the corresponding chord coincide.
- The tangent at any point of a circle is perpendicular to the radius through the point of contact.

- A line drawn through the end of a radius (point on circumference) and perpendicular to it is a tangent to the circle.
- There is no tangent to a circle passing through a point lying inside the circle.
- There are exactly two tangents to a circle through a point outside the circle.
- At any point on the circle there can be one and only one tangent.
- The length of the segment of the tangent from the external point P and the point of contact with the circle is called the length of the tangent.
- The lengths of tangents drawn from an external point to the circle are equal.
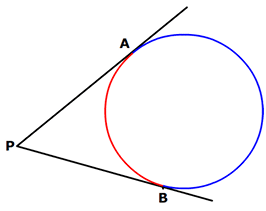 The figure shows two equal tangents (PA = PB) from an external point P.
The figure shows two equal tangents (PA = PB) from an external point P. - The centre of a circle lies on the bisector of the angle between the two tangents.
- A common tangent is called a direct common tangent if both the circles lie on the same side of it.
- The two direct common tangents are equal in length.
- The length of a direct common tangent to two circles is
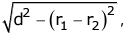 where d is the distance between the centres of the circles and r1 and r2 are the radii of the circles.
where d is the distance between the centres of the circles and r1 and r2 are the radii of the circles. - A common tangent is called transverse common tangent if the circles lie on opposite sides of it.
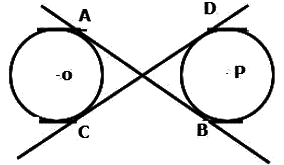 In this figure AB and CD are two transverse common tangent.
In this figure AB and CD are two transverse common tangent.
The two transverse common tangents are equal in length.
Segment of a chord and its properties
- If two chords of a circle intersect internally or externally, then the products of the lengths of segments are equal.
- If two line segments AB and CD intersect at P or lines containing segments AB and CD intersect at P such that PA x PB = PC x PD, then the four points A, B, C and D are concyclic.
- If a line touches a circle and from the point of contact a chord is drawn, the angles between the tangent and the chord are respectively equal to the angles in the corresponding alternate segment.
- If a line is drawn through an end of a chord of a circle so that the angle formed with the chord is equal to the angle subtended by the chord in the alternate segment, then the line is a tangent to the circle.
- If a chord and a tangent intersect externally then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection, that is PA x PB = PT2
The document Revision Notes: Circle: Tangents and Intersecting Chords | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|198 docs|30 tests
|
FAQs on Revision Notes: Circle: Tangents and Intersecting Chords - Mathematics Class 10 ICSE
| 1. What are tangents to a circle, and how do they relate to the radius? |  |
Ans. A tangent to a circle is a straight line that touches the circle at exactly one point. This point is known as the point of tangency. The key property of tangents is that they are perpendicular to the radius of the circle at the point of tangency. This means that if you draw a radius to the point where the tangent touches the circle, the angle between the tangent and the radius will be 90 degrees.
| 2. What is the relationship between two intersecting chords in a circle? |  |
Ans. When two chords intersect inside a circle, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord. If chord AB intersects chord CD at point E, then the relationship can be expressed as AE × EB = CE × ED. This property is very useful for solving problems involving intersecting chords.
| 3. How can you find the length of a tangent from an external point to a circle? |  |
Ans. The length of a tangent drawn from an external point to a circle can be found using the Pythagorean theorem. If you have a circle with center O and a point P outside the circle, the length of the tangent PT (where T is the point of tangency) can be calculated using the formula PT = √(OP² - r²), where OP is the distance from point P to the center O of the circle, and r is the radius of the circle.
| 4. Can you explain the tangent-secant theorem? |  |
Ans. The tangent-secant theorem states that if a tangent and a secant are drawn from a point outside the circle, then the square of the length of the tangent segment is equal to the product of the whole secant segment and its external part. If PT is the tangent from point P to circle O and PS is the secant that intersects the circle at points S and Q, then the relationship can be expressed as PT² = PS × PQ, where PS is the entire secant and PQ is the external segment.
| 5. What are the key properties to remember when dealing with tangents and intersecting chords in circles? |  |
Ans. Key properties include:
1. A tangent is perpendicular to the radius at the point of tangency.
2. The lengths of two intersecting chords are related by the product of their segments.
3. The tangent-secant theorem connects the lengths of the tangent and secant from an external point.
4. The angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
These properties are essential for solving problems related to tangents and intersecting chords in circles.
Related Searches















