Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Equation of A Line
Revision Notes: Equation of A Line | Mathematics Class 10 ICSE PDF Download
Important Concepts
- The angle which a straight line makes with the positive direction of x-axis measured in the anticlockwise direction is called the inclination (or angle of inclination) of the line. The inclination is usually denoted by θ.
- If θ is the inclination of a line l, then tan θ is called the slope or gradient of the line l.
- The slope of a line whose inclination is 90° is not defined.
- The slope of x-axis is zero and slope of y-axis is not defined.
- Three points A, B and C are collinear if Slope of AB = slope of BC.
- Let AB be a line cutting x-axis and the y-axis at A(a, 0) and B(0, b) respectively. Then the intercepts made on the axes are a and b respectively. That is, x-intercept = a and y-intercept = b.
- The equation of line parallel to x-axis at a distance a in the positive direction of y-axis is y = a and in negative direction of y-axis is y = -a.
Slope of a line
The slope m of the line through the points (x1, y1) and (x2, y2) is given by m =
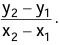
Parallel and Perpendicular Lines
- Two non-vertical lines l and m are parallel if and only if their slopes are equal.
That is m1 = m2 - Two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other.
That is m2 = (-1)/m1 ⇒ m1 x m2 = -1
Condition for Collinearity of Points
Three points A, B and C are collinear if Slope of AB = slope of BC
Equation of coordinate axes
- The equation of x-axis is y = 0
- The equation of y-axis is x = 0
Various Forms of the Equations of Straight Lines
- Slope-intercept form: The equation of a line having slope m and y-intercept c is given by y = mx + c.
- Point-Slope form: The equation of a line passing through (x1, y1) and having slope m is given by
y - y1 = m(x - x1). - Two-point form: The equation of line passing through two points A(x1, y1) and B(x2, y2) is given by
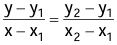
The document Revision Notes: Equation of A Line | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|213 docs|30 tests
|
FAQs on Revision Notes: Equation of A Line - Mathematics Class 10 ICSE
| 1. What is the general form of the equation of a line? |  |
Ans. The general form of the equation of a line in a two-dimensional Cartesian coordinate system is given by \( Ax + By + C = 0 \), where \( A \), \( B \), and \( C \) are constants, and \( A \) and \( B \) cannot both be zero.
| 2. How do you find the slope of a line given two points? | |
Ans. The slope \( m \) of a line that passes through two points \( (x_1, y_1) \) and \( (x_2, y_2) \) can be calculated using the formula \( m = \frac{y_2 - y_1}{x_2 - x_1} \). This gives the rate of change of \( y \) with respect to \( x \).
| 3. What is the slope-intercept form of a line, and how is it used? | |
Ans. The slope-intercept form of a line is expressed as \( y = mx + b \), where \( m \) is the slope of the line and \( b \) is the y-intercept (the point where the line crosses the y-axis). This form is useful for quickly graphing a line and understanding its characteristics.
| 4. How can you convert the general form of a line equation to slope-intercept form? | |
Ans. To convert the general form \( Ax + By + C = 0 \) to slope-intercept form \( y = mx + b \), you isolate \( y \) on one side of the equation. Rearranging gives \( By = -Ax - C \) and then dividing by \( B \) results in \( y = -\frac{A}{B}x - \frac{C}{B} \). Here, \( m = -\frac{A}{B} \) and \( b = -\frac{C}{B} \).
| 5. What are the different ways to represent the equation of a line? | |
Ans. The equation of a line can be represented in several forms: the general form \( Ax + By + C = 0 \), the slope-intercept form \( y = mx + b \), the point-slope form \( y - y_1 = m(x - x_1) \) (where \( (x_1, y_1) \) is a point on the line), and in parametric form. Each representation is useful in different mathematical contexts.
About this Document
4.98/5
Rating
Sep 29, 2025
Last updated
Document Description: Revision Notes: Equation of A Line for Class 10 2025 is part of Mathematics Class 10 ICSE preparation.
The notes and questions for Revision Notes: Equation of A Line have been prepared according to the Class 10 exam syllabus. Information about Revision Notes: Equation of A Line covers topics
like and Revision Notes: Equation of A Line Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes: Equation of A Line.
Introduction of Revision Notes: Equation of A Line in English is available as part of our Mathematics Class 10 ICSE
for Class 10 & Revision Notes: Equation of A Line in Hindi for Mathematics Class 10 ICSE course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Revision Notes: Equation of A Line | Mathematics Class 10 ICSE
Description
Full syllabus notes, lecture & questions for Revision Notes: Equation of A Line | Mathematics Class 10 ICSE - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics Class 10 ICSE | Best notes, free PDF download
Information about Revision Notes: Equation of A Line
In this doc you can find the meaning of Revision Notes: Equation of A Line defined & explained in the simplest way possible. Besides explaining types of
Revision Notes: Equation of A Line theory, EduRev gives you an ample number of questions to practice Revision Notes: Equation of A Line tests, examples and also practice Class 10
tests
Related Searches
Important questions
,MCQs
,practice quizzes
,Previous Year Questions with Solutions
,mock tests for examination
,Extra Questions
,Free
,Revision Notes: Equation of A Line | Mathematics Class 10 ICSE
,shortcuts and tricks
,ppt
,Exam
,Viva Questions
,Revision Notes: Equation of A Line | Mathematics Class 10 ICSE
,study material
,past year papers
,video lectures
,Revision Notes: Equation of A Line | Mathematics Class 10 ICSE
,Objective type Questions
,Summary
,Semester Notes
,Sample Paper
;
Additional Information about Revision Notes: Equation of A Line for Class 10 Preparation
Revision Notes: Equation of A Line Free PDF Download
The Revision Notes: Equation of A Line is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes: Equation of A Line now and kickstart your journey towards success in the Class 10 exam.
Importance of Revision Notes: Equation of A Line
The importance of Revision Notes: Equation of A Line cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes: Equation of A Line
Revision Notes: Equation of A Line Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes: Equation of A Line.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes: Equation of A Line Notes on EduRev are your ultimate resource for success.
Revision Notes: Equation of A Line Class 10 Questions
The "Revision Notes: Equation of A Line Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes: Equation of A Line on the App
Students of Class 10 can study Revision Notes: Equation of A Line alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes: Equation of A Line,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes: Equation of A Line is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup