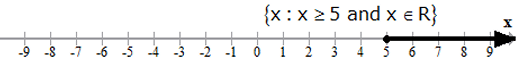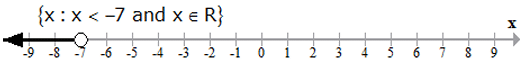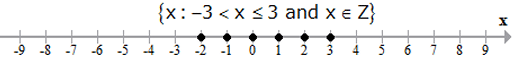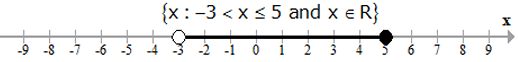Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Linear Inequations
Revision Notes: Linear Inequations | Mathematics Class 10 ICSE PDF Download
Introduction to inequations
- An inequation is a mathematical statement which states that one quantity is not equal to the other.
- In an inequation, the signs, '< ',' > ',' ≤ ' and '≥'are called signs of inequality.
Rules for solving inequations algebraically
- On transferring a positive term (the term in addition) from one side of an inequation to its other side, the sign of the term becomes negative.
Example: 5x + 3 ≤ 13 ⇒ 5x ≤ 13 - 3 - On transferring a negative term from one side of an inequation to its other side, the sign of the term becomes positive.
Example: 5x - 3 ≤ 13 ⇒ 5x ≤ 13 + 3 - If each term of an inequation be multiplied or divided by the same positive number, the sign of inequality remains the same.
Case I: If p is positive and x < y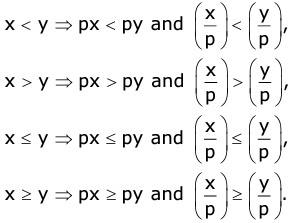 Example: 2x ≤ 5 ⇒ 2 x 2x ≤ 2 x 5 ⇒ 4x ≤ 10
Example: 2x ≤ 5 ⇒ 2 x 2x ≤ 2 x 5 ⇒ 4x ≤ 10 - If each term of an inequation be multiplied or divided by the same negative number, the sign of inequality reverses.
Case II: If p is negative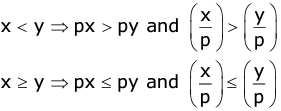
Example: x ≤ -2 ⇒ (-3) x x ≥ (-3) x (-2) ⇒ -3x ≥ 6 - If sign of each term on both the sides of an inequation is changed, the sign of inequality gets reversed.
Example: -3x ≥ 20 ⇒ 3x ≤ -2 - If both the sides of an inequation are positive and both are negative, then on taking their reciprocals, the sign of inequality reverses.
Example: If x and y both are either positive or both are negative, then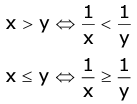
- The sign of the inequality does not change when a positive number is added or subtracted from both sides.
i. If x < y, then x+a < y+a.
ii. If x< y, then x-a < y-a.
Replacement Set and Solution Set
- Replacement set is the set from which the values of the variable involved in the inequation are chosen.
- Solution set is the subset of the replacement set, whose elements satisfy the given inequation.
Example: Let the given inequation be x ≤ 4, if:
i. the replacement set = N, the set of natural numbers; the solution set = {1, 2, 3, 4}
ii. the replacement set = W, the set of whole numbers; The solution set = {0, 1, 2, 3, 4}
iii. the replacement set = Z or I, the set of Integers; The solution set = {….-2, -1, 0, 1, 2, 3, 4}
iv. the replacement set = R, the set of real numbers; The solution set = {x : x ∈ R and x ≤ 4) - The solution set depends on the replacement set.
Representation of the solution on the number line
i. The solution set of an inequation can be represented on a real number line.
ii. A hollow circle marks the end of a range with a strict inequality (< or >) .
iii. A darkened circle marks the end of a range involving an equality as well (≤ or ≥).
iv. Some examples:
The document Revision Notes: Linear Inequations | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|276 docs|8 tests
|
FAQs on Revision Notes: Linear Inequations - Mathematics Class 10 ICSE
| 1. What are linear inequations and how do they differ from linear equations? |  |
Ans. Linear inequations are mathematical statements that express a relationship where one expression is not equal to another, using inequality signs such as <, >, ≤, or ≥. Unlike linear equations, which assert that two expressions are equal (using the = sign), linear inequations allow for a range of possible solutions rather than a single solution.
| 2. How do you solve a linear inequation algebraically? |  |
Ans. To solve a linear inequation algebraically, follow these steps:
1. Isolate the variable on one side of the inequation, similar to solving equations.
2. If you multiply or divide both sides by a negative number, remember to reverse the inequality sign.
3. Simplify the expression to find the solution set, which may be expressed using interval notation or set notation.
| 3. What is the significance of the replacement set and solution set in inequations? |  |
Ans. The replacement set is the set of all possible values that can be substituted into the inequation. The solution set, on the other hand, is the subset of the replacement set that satisfies the inequation. Understanding these sets helps in identifying which values are valid solutions and visualizing the results on a number line.
| 4. How can you represent the solution of a linear inequation on a number line? |  |
Ans. To represent the solution of a linear inequation on a number line, first, determine the critical points (where the inequation equals zero). Then, shade the regions that satisfy the inequation. Use open circles for inequalities that do not include the endpoint (e.g., < or >) and closed circles for those that do (e.g., ≤ or ≥).
| 5. Can you provide an example of a linear inequation and its solution? |  |
Ans. Certainly! Consider the linear inequation 2x - 3 < 5. To solve it, first add 3 to both sides: 2x < 8. Then, divide by 2: x < 4. The solution set is all values less than 4, which can be represented on the number line with an open circle at 4 and shading to the left.
Related Searches