Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Mensuration: Cylinder, Cone and Sphere
Revision Notes: Mensuration: Cylinder, Cone and Sphere | Mathematics Class 10 ICSE PDF Download
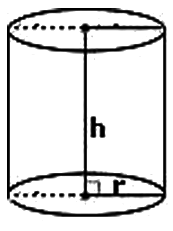
Right Circular Cylinder
A solid having uniform circular cross-section is called a cylinder.
If r and h respectively denote the radius of the circular cross-section and the height of the cylinder, then
Area of cross-section = πr²
Perimeter of cross-section = 2πr
Area of curved surface or lateral surface area = Perimeter of cross-section x Height = 2πrh
Total surface area = Curved surface area + 2(Area of cross-section)
= 2πrh + 2πr²
= 2πr(h + r)
Volume = Area of cross-section x Height = πr²h
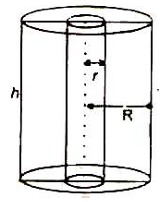
Right Circular Hollow Cylinder
If R and r respectively denote the external and internal radii of a right circular hollow cylinder and h denotes its height, then
Thickness of its wall = R – r
Area of cross-section = πR2 – πr2 = π(R2 – r2)
External curved surface = 2πRh
Internal curved surface = 2πrh
Total surface area = External curved surface area + Internal curved surface area + 2(Area of cross section)
= 2πRh + 2πrh + 2π(R² - r²)
Volume of material = External volume – Internal volume
= πR²h – πr²h)
= π(R² – r²)h
Right circular cone
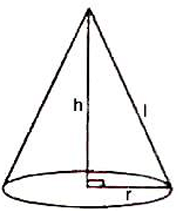 If r, h and l respectively denote the radius, height and slant height of a right circular cone, then
If r, h and l respectively denote the radius, height and slant height of a right circular cone, then
Slant height (l) = 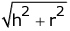
Area of curved surface = πrl
Total surface area = Area of curved surface + Area of base
= πrl + πr²
= πr(l + r)
Volume = (1/3) πr2h
Sphere
If r is the radius of the sphere, then
Surface area = 4πr²
Volume = 4/3 πr3
 Spherical shell
Spherical shell
If R is the external radius and r is the internal radius of a spherical shell, then
Surface area (outer) = 4πR²
Volume of material = 
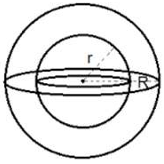
Hemisphere
If r is the radius of the hemisphere, then
Total surface Area = 1/2 x Surface area of sphere + Area of base
= (1/2) x 4πr2 + πr2
= 3πr2
Volume = (1/2) x Volume of sphere
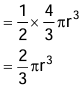
Conversion of Solids
When a solid is melted and converted to another, volume of both the solids remains the same, assuming there is no wastage in the conversions.
However, the surface area of the two solids may or may not be the same.
Combination of Solids
The total surface area of the solid formed by the combination of solids is the sum of the curved surface area of each of the individual solids.
The volume of the solid formed by the combination of basic solids is the sum of the volumes of each of the basic solids.
The document Revision Notes: Mensuration: Cylinder, Cone and Sphere | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|292 docs|30 tests
|
FAQs on Revision Notes: Mensuration: Cylinder, Cone and Sphere - Mathematics Class 10 ICSE
| 1. What is the formula for the volume of a cylinder? |  |
Ans. The volume \( V \) of a cylinder can be calculated using the formula:
\[ V = \pi r^2 h \]
where \( r \) is the radius of the base, \( h \) is the height of the cylinder, and \( \pi \) is approximately 3.14.
| 2. How do you calculate the surface area of a cone? |  |
Ans. The surface area \( A \) of a cone is given by the formula:
\[ A = \pi r (r + l) \]
where \( r \) is the radius of the base, \( l \) is the slant height, and \( \pi \) is approximately 3.14. The surface area includes the base area and the lateral surface area.
| 3. What are the formulas for finding the volume and surface area of a sphere? |  |
Ans. The volume \( V \) of a sphere is calculated using the formula:
\[ V = \frac{4}{3} \pi r^3 \]
where \( r \) is the radius of the sphere.
The surface area \( A \) of a sphere is given by the formula:
\[ A = 4\pi r^2 \]
where \( r \) is the radius.
| 4. How do you derive the relationship between the height and radius in a right circular cone? |  |
Ans. In a right circular cone, the height \( h \) and the radius \( r \) are related through the slant height \( l \) using the Pythagorean theorem:
\[ l = \sqrt{r^2 + h^2} \]
This formula helps in calculating any of the three dimensions if the other two are known.
| 5. What is the importance of π (pi) in the calculations of cylinders, cones, and spheres? |  |
Ans. The number \( \pi \) (approximately 3.14) is crucial in mensuration as it represents the ratio of the circumference of a circle to its diameter. In the formulas for volume and surface area of cylinders, cones, and spheres, \( \pi \) is essential for relating linear measurements (like radius) to area and volume, which are two-dimensional and three-dimensional measures respectively.
Related Searches
















