Class 10 Exam > Class 10 Notes > Mathematics Class 10 ICSE > Revision Notes: Quadratic Equations
Revision Notes: Quadratic Equations | Mathematics Class 10 ICSE PDF Download
Important Concepts
- If p(x) is a quadratic polynomial, then p(x) = 0 is called a quadratic equation.
The general form of a quadratic equation, in the variable x, is ax2 + bx + c = 0, where a, b, c are real numbers and a ≠ 0. - The value of x that satisfies an equation is called the zeroes or roots of the equation.
A real number α is said to be a solution/root of the quadratic equation ax2 + bx + c = 0
if aα2 + bα + c = 0. - A quadratic equation has at most two zeros.
Nature of the roots of a quadratic equation
The nature of the roots of a quadratic equation depends upon the value of discriminant b2 – 4ac.
i. If b2 – 4ac > 0, the roots are real and unequal
ii. If b2 – 4ac = 0, the roots are real and equal
iii. If b2 – 4ac < 0, the roots are imaginary (not real)
If ax2 + bx + c, a ≠ 0, can be reduced to the product of two linear factors, then the roots of the quadratic equation ax2 + bx + c = 0 can be found by equating each factor to zero.
Solution of Quadratic Equation by Factroisation
Example, Solve the equation (9/2)x = 5 + x2 by factorization:
Step 1: Clear all fractions and brackets, if necessary
9x = 2(5 + x2)
Step 2: Transpose all the terms to the left hand side to get an equation in the form ax2 + bx + c = 0
9x = 2x2 + 10
⇒ 2x2 - 9x +10 = 0
Step 3: Factorise the expression on the left hand side.
2x2 - 9x + 10 = 0
⇒ 2x2- 5x - 4x +10 = 0
⇒ x (2x - 5) -2 (2x - 5) = 0
⇒ (x - 2)(2x - 5) = 0
Step 4: Put each factor equal to zero and solve
(x - 2) (2x - 5) = 0
⇒ x - 2 = 0, (2x - 5) = 0
⇒ x = 2; 2x = 5
⇒ x = 2; x = 5/2
Thus, we have, x = 2 or x = 5/2
Solution of Quadratic Equation by Quadratic Formula
The roots of a quadratic equation ax2+ bx + c = 0 (a ≠ 0) can be calculated by using quadratic formula:
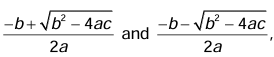 where b2 - 4ac ≥ 0
where b2 - 4ac ≥ 0
Equations Reducible to Quadratic Form
There are many equations which are not in the quadratic form but can be reduced to quadratic form by simplifications.
Let us solve the equation x4 - 2x2 - 3 = 0
It is clear that the above equation is not a quadratic equation.
Now assume that x2 = y
Then rewrite the given quadratic equation as,
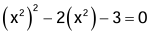
Substituting in the above equation, we have y2 - 2y - 3 = 0
This is a quadratic equation in y.
Let us solve the quadratic equation through factorization.
y2 - 2y - 3 = 0
⇒ y2 - 3y + y - 3 = 0
⇒ y (y - 3) +(y - 3) = 0
⇒ (y + 1)(y - 3) = 0
⇒ y + 1 = 0 or y - 3 = 0
⇒ y = -1 or y = 3
Applications of quadratic equation in solving real life problems
Following points can be helpful in solving word problems:
i. Every two digit number ‘xy’ where x is a ten’s place and y is a unit’s place can be expressed as
xy = 10x + y
ii. Downstream: It means that the boat is running in the direction of the stream
Upstream: It means that the boat is running in the opposite direction of the stream
Thus, if
Speed of boat in still water is x km/h
And the speed of stream is y km/h
Then the speed of boat downstream will be (x + y) km/h and in upstream it will be (x − y) km/h.
iii. If a person takes x days to finish a work, then his one day's work = 1/x
The document Revision Notes: Quadratic Equations | Mathematics Class 10 ICSE is a part of the Class 10 Course Mathematics Class 10 ICSE.
All you need of Class 10 at this link: Class 10
|
74 videos|213 docs|30 tests
|
FAQs on Revision Notes: Quadratic Equations - Mathematics Class 10 ICSE
| 1. What are the different types of roots of a quadratic equation? |  |
Ans.The roots of a quadratic equation can be classified into three types based on the discriminant (D = b² - 4ac):
1. <b>Real and Distinct Roots:</b> If D > 0, the equation has two different real roots.
2. <b>Real and Equal Roots:</b> If D = 0, the equation has exactly one real root (a repeated root).
3. <b>Complex Roots:</b> If D < 0, the equation has two complex roots which are conjugates of each other.
| 2. How can we reduce an equation to quadratic form? |  |
Ans.An equation can often be transformed into a quadratic form by substituting variables or rearranging terms. For instance, if you have an equation involving a term like x², you can let y = x or another suitable substitution that simplifies the original equation into a standard quadratic form (ax² + bx + c = 0). Solving for y can then lead to solving the quadratic equation.
| 3. How do you apply quadratic equations to solve real-life problems? |  |
Ans.Quadratic equations can be applied to various real-life situations such as projectile motion, area problems, and profit maximization. For example, if you need to determine the maximum height reached by a ball thrown upwards, the height as a function of time can be modeled by a quadratic equation. By finding the vertex of the parabola represented by the quadratic equation, you can find the maximum height.
| 4. What is the significance of the discriminant in a quadratic equation? |  |
Ans.The discriminant (D = b² - 4ac) is crucial as it determines the nature of the roots of the quadratic equation. It helps predict whether the roots are real and distinct, real and equal, or complex. This understanding aids in graphing the quadratic function and analyzing its behavior without solving the equation completely.
| 5. Can all quadratic equations be solved using the quadratic formula? |  |
Ans.Yes, all quadratic equations can be solved using the quadratic formula, which is given by x = (-b ± √D) / (2a), where D is the discriminant. This formula works for any quadratic equation of the form ax² + bx + c = 0, providing a systematic way to find the roots, regardless of whether they are real or complex.
Related Searches
















