Schrödinger Wave Equation & Wavefunction | Chemistry Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Interpretation of the Wavefunction |

|
| Normalization of the Wavefunction |

|
| Solved Example |

|
Introduction
- In 1926, the Austrian physicist Erwin Schrödinger formulated what came to be known as the (time-dependent) Schrödinger Equation:
 (4.7.1)
(4.7.1) - Equation 4.7.1 effectively describes matter as a wave that fluctuates with both displacement and time. Since the imaginary portion of the equation dictates its time dependence, it is sufficed to say that for most purposes it can be treated as time-independent. The result is seen in Equation 4.7.2:
 (4.7.2)
(4.7.2) - Although this time-independent Schrödinger Equation can be useful to describe a matter wave in free space, we are most interested in waves when confined to a small region, such as an electron confined in a small region around the nucleus of an atom. Several different models have been developed that provide a means by which to study a matter-wave when confined to a small region: the particle in a box (infinite well), finite well, and the Hydrogen atom. We will discuss each of these in order to develop a greater understanding for how a wave behaves when it is in a bound state.
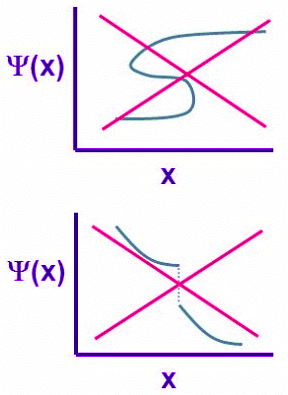
Figure 4.7.1: Two unacceptable wavefunctions. (left) This is not a single-valued function and (right) this is a non-continuous function
Four general aspects are applicable to an acceptable wavefunction:
- An acceptable wave function will be the solution of the Schrödinger equation (either Equations 4.7.1 or 4.7.2).
- An acceptable wavefunction must be normalizable so will approaches zero as position approaches infinity.
- An acceptable wave function must be a continuous function of position.
- An acceptable wavefunction will have a continuous slope (Figure 4.7.1).
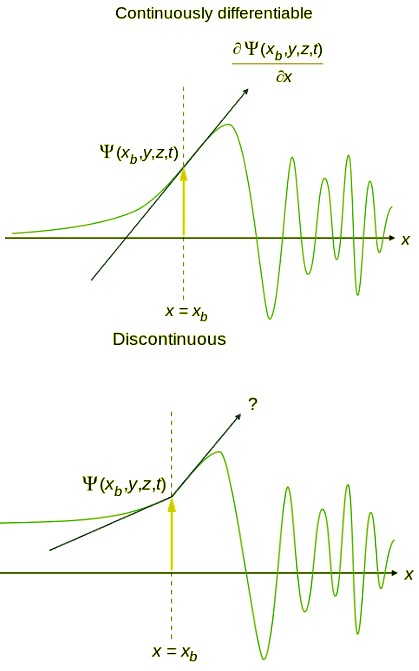
Figure 4.7.2: Wavefunction continuity in space
Interpretation of the Wavefunction
- Since wavefunctions can in general be complex functions, the physical significance cannot be found from the function itself because the √−1 is not a property of the physical world. Rather, the physical significance is found in the product of the wavefunction and its complex conjugate, i.e. the absolute square of the wavefunction, which also is called the square of the modulus.
ψ∗(r,t) ψ(r,t) = |ψ (r,t)|2 (4.7.3) - where r is a vector (x, y, z) specifying a point in three-dimensional space. The square is used, rather than the modulus itself, just like the intensity of a light wave depends on the square of the electric field. At one time it was thought that for an electron described by the wavefunction ψ(r) , the quantity eψ∗(ri) ψ(ri)dτ was the amount of charge to be found in the volume dτ located at ri . However, Max Born found this interpretation to be inconsistent with the results of experiments.
- The Born interpretation, which generally is accepted today, is that ψ ∗ (ri)ψ(ri)dτ is the probability that the electron is in the volume dτ located at ri . The Born interpretation therefore calls the wavefunction the probability amplitude, the absolute square of the wavefunction is called the probability density, and the probability density times a volume element in three-dimensional space (dτ) is the probability. The idea that we can understand the world of atoms and molecules only in terms of probabilities is disturbing to some, who are seeking more satisfying descriptions through ongoing research.
Normalization of the Wavefunction
A probability is a real number between 0 and 1. An outcome of a measurement that has a probability of 0 is an impossible outcome, whereas an outcome that has a probability of 1 is certain. The probability of a measurement of x yielding a result between −∞ and +∞ is
 (4.7.4)
(4.7.4)
However, a measurement of x must yield a value between −∞ and +∞ , since the particle has to be located somewhere. It follows that Px∈−∞:∞(t) = 1, or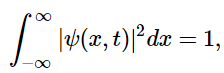 (4.7.5)
(4.7.5)
which is generally known as the normalization condition for the wavefunction.
Solved Example
Example: Normalize the wavefunction of a Gaussian wave packet, centered on x = xo, and of characteristic width σ: i.e.,
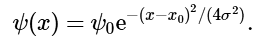 (4.7.6)
(4.7.6)
Ans: To determine the normalization constant ψ0, we simply substitute Equation 4.7.6 into Equation 4.7.5, to obtain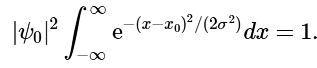 (4.7.7)
(4.7.7)
Changing the variable of integration to y = (x − x0)/(√2 – σ), we get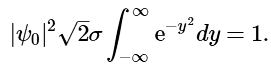 (4.7.8)
(4.7.8)
However,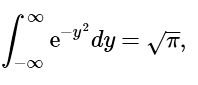 (4.7.9)
(4.7.9)
which implies that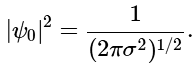 (4.7.10)
(4.7.10)
Hence, a general normalized Gaussian wavefunction takes the form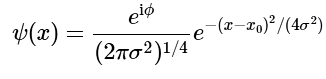 (4.7.11)
(4.7.11)
where ϕ is an arbitrary real phase-angle.
FAQs on Schrödinger Wave Equation & Wavefunction - Chemistry Optional Notes for UPSC
| 1. What is the wavefunction in quantum mechanics? |  |
| 2. How is the wavefunction interpreted in quantum mechanics? |  |
| 3. What is the normalization of the wavefunction? |  |
| 4. What is the Schrödinger wave equation? |  |
| 5. How are the Schrödinger wave equation and wavefunction used in the UPSC exam? |  |

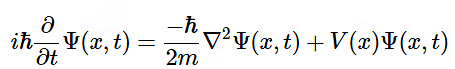 (4.7.1)
(4.7.1)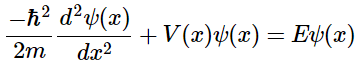 (4.7.2)
(4.7.2)
















