Series | SSC CGL Tier 2 - Study Material, Online Tests, Previous Year PDF Download

What is a Series / Sequence? 

A series or sequence consists of several terms. In other words, the unit of a sequence is called a term. Each term in the series has its own importance as there exists a certain relationship between the two consecutive/alternating terms. 

• This relationship is repeated in the series and based on this relationship; we are required to find out the missing term. We come across several types of questions based on any given series.

• Base on whether the series consists of the alphabets or the numerals (numbers) or the words, the series can be classified into the following types:
  (i) Number series                      
  (ii) Alphabet series                              
  (iii) Mixed series      
• It is quite easy to decipher an alphabetic series as it is easy to remember the place of alphabet in the series. In the case of number series also the pattern can be found out but in case of mixed series or jumbled series, it is very difficult to remember the position of each term.
• A mixed series comprises letters, numbers and symbols and unlike the English alphabet series, the number of terms is not fixed in such series. A mixed series may contain any number of terms viz. 23, 24, 26, 28, 30, 31 or 32. Such questions require sufficient practice as there are no definite shortcuts for these questions. 
• The questions on mixed series can be divided into two major heads:
  (a) Series of letters and numbers.
  (b) Series of letters, numbers and symbols.
• In questions based on mixed series, one is required to judge and find out the relationship between the given terms and find out the answer. To begin with, count the terms and find out the relationship between the required terms.

Some Important Tips

• First of all, count the terms in the given series.
• Break up the series into groups of threes/fours depending on the requirements of the question.
• Pin-point the middle term, if the number of countable terms is odd.
• Write down the total number of letters, numbers and symbols respectively.
• Form the groups of five terms, counting from either end so that you can recognize the position of the required term quickly.

Numerical Series

• Analysis of Numerical Series: A close analysis of the above examples show that the number series can be of the following types.
• Pure Series: In this type, the number follows a pattern which can be easily understood. The number itself may be:
  (a) Perfect square                                                
  (b) Perfect cube
  (c) Prime number                                                
  (d) Combination
• Difference Series: The difference series in of the first number with the next number makes a series.

Ex: 1, 3, 5, 7, 9, 11, ……. The difference between two consecutive numbers is 2. So it makes a series.
Ex: 1, 2, 4, 7, 11, 16……. The difference between the consecutive number is 1, 2, 3, 4, 5 and so on it also makes a perfect series.

Solved Examples of Numerical Series

Example 1: Which is the number that comes next in the sequence?

1,  5,  13,  29, __ , 125

(a) 32    
(b) 62      
(c) 61  
(d) 31         

The correct answer is option (c).                              

Sol. In this case, the series is increasing by +4, +8, +16, +32, +64. So our answer is 61, as by adding the number 32 to 29 we get the required number, i.e. 61.
Example 2: 1,  4,  9, 16,  25, __ ? 

(a) 35  
(b) 36  
(c) 48  
(d) 49           

The correct answer is option (b).                            

Sol. The numbers are: 1²,  2²,  3³,  4²,   5²

Hence 6² = 36.   
Example 3: Which is the number that comes next in the sequence?

6, 11, 21, 36, 56, __

(a) 42  
(b) 51  
(c) 81  
(d) 91

The correct answer is option (c).                                         

The answer here is 81 because the series is progressing by a factor of 5,10,15, 20, 25.
Example 4:  Which is the number that comes next in the sequence?

 0,  6,  24,  60,  120,  210, ___ ?

(a) 240  
(b) 290  
(c) 336  
(d) 504    

The correct answer is option (d).               

Sol.  Clearly, the given series is: 1³ – 1,  2³ – 2,  3³ – 3,  4³ – 4,  5³ – 5,  6³ – 6.

Next number = 7³ – 7 = 343 – 7 = 336.

Alphabet Series

• In problems based on alphabet series, the pattern of the alphabet in the series is to be deducted and the next term is to be found out. There are no set rules, yet the problems can easily be solved if the place number of each alphabet is memorized. Like for K’s place value in the alphabet sequence is 11 and that of V is 22, that of Q is 17 and X is 24. If these places are known, the questions become easy to solve.
• There can be omission of alphabets one each time. Alphabets may be omitted in an increasing order or decreasing order;  for example one each time or two each time or three each time and so on. There can also be alternate order such as first one alphabet is skipped, then two may be skipped and then three may be omitted. 
• The skipping pattern may be of two types:
  (i) Regular Order: In this case, the number of alphabets skipped remain the same through the series.
  (ii) Increasing Order: Each time the number of alphabets skipped increase in a given pattern.
• The theory can only be understood with the help of practical examples only.

Solved Examples of Alphabet Series

Example 5: What terms will fill the blank spaces?
A,  B,  C,  D,  E, (….), (….)                                                                                                   (a) O, K  
(b) N, M  
(c) K, S  
(d) F, G  

The correct answer is option (d).         

Sol. The given series consists of alphabets in their original order. So, the missing terms would be (d) F and G. 
Example 6: What terms will fill the blank spaces?

Z,  X,  V,  T,  R, (…), (…)                                                                                             

(a) O, K  
(b) N, M  
(c) K, S  
(d) P, N      

The correct answer is option (d).       

Sol. Clearly, the given series consists of alternate letters in reverse order. The alphabets are skipped one at a time. So, the missing terms would be (d) P and N. 
Example 7: Find the missing alphabet: B, D, G, K, P, (…), (…)

Sol. Each time the number of letters skipped increases by one. So the answer here is V.

B is the second alphabet in the series, D is fourth in the series, G is seventh, K is eleventh, P is sixteenth and so the next will be twenty second i.e. V of the series.
Example 8: Find the missing term:   
OTE,  PUF,  QVG,  RWH, (….)                                                                         

(a) SYJ    
(b) TXI    
(c) SXJ    
(d) SXI

The correct answer is option (d). 

Sol. The first letters of the terms are in alphabetical order, and so are second and third letters. 

OPQRS,  TUVWX,   EFGHI                                                                               

Mixed Series 

• Series consisting of both letters & numbers.

Directions (9– 10): Study the following arrangement carefully and answer the questions given below:

W 1 5 E J R 2 M A 9 T K U N 4 B I 8 D H 3 F 6 P Z 7 Q

Example 9: How many such consonants are there, each of which is immediately preceded by a number and immediately followed by a vowel?

(a) None    
(b) One  
(c) Two    
(d) Three              

The correct answer is option (c).  

Example 10: Which of the following is the seventh to the left of 4?

(a) M
(b) A
(c) F
(d) 3                        

The correct answer is option (a).  

Question for Series

Try yourself:Find the missing character?

• A.

  10C
• B.

  12C
• C.

  13C
• D.

  7C

Explanation

In each row, A, B and C, each of these must appear once.
First column ==> 4*7 = 28.
Third column ==> 3*15 = 45.
Second Column ==> 2*5 = 10. So,
Missing Character = 10C.

Report a problem

Cancel Report

View Solution

Series Consisting of Letters, Numbers and Symbols

• In order to make series more complicated, letters and numbers are combined with different symbols. 

Examples:

Directions (11 –12): Study the following arrangement carefully and answer the questions given below :

K P 5 # 7 M N E 2 D A ¶ 4 F H I T 9 1 $ U 6% W 3

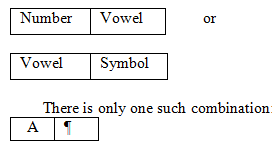
Example 11:  How many such vowels are there in the above arrangement, each of which is either immediately preceded by a number or immediately followed by a symbol?

(a) None
(b) One
(c) Two
(d) Three    

The correct answer is option (b).        

Example 12: Which of the following is the sixth to the right of the fifteenth element from right end in the above arrangement?

(a) T
(b) 7
(c) 2
(d) U                

The correct answer is option (a).  

15^th element from right Þ A

 6^th to right of A Þ T

Required element =15 – 6 = 9^th term from right.

Miscellaneous Type Questions

Example 13: How many such digits are there in the number 82134967 each of which is as far away from the beginning of the number as when they are arranged in descending order?

(a) None
(b) One
(c) Two
(d) Three                

The correct answer is option (b).  

4 is such number in the series which is at the same position in the original and also when arranged in descending order.