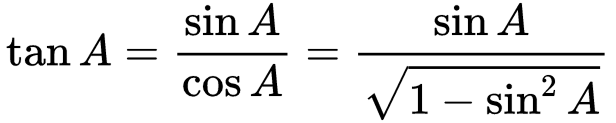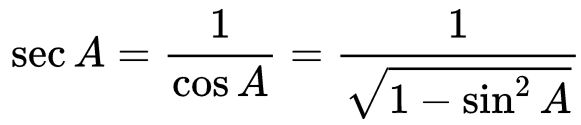Introduction to Trigonometry Class 10 Notes Maths Chapter 8
Terminologies related to Trigonometry
- Trigonometry is the science of relationships between the sides and angles of a right-angled triangle.
- Ratios of sides of right triangle are called trigonometric ratios.
- Consider triangle ABC right-angled at B. These ratios are always defined with respect to acute angle ‘A’ or angle ‘C.
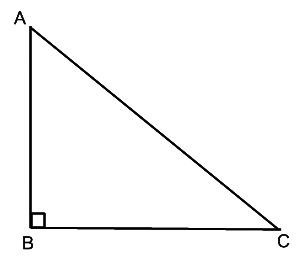
- If one of the trigonometric ratios of an acute angle is known, the remaining trigonometric ratios of an angle can be easily determined.
Trigonometric Ratios
How to identify sides?Identify the angle with respect to which the t-ratios have to be calculated. Sides are always labelled with respect to the ‘θ’ being considered.
Let us take two cases:
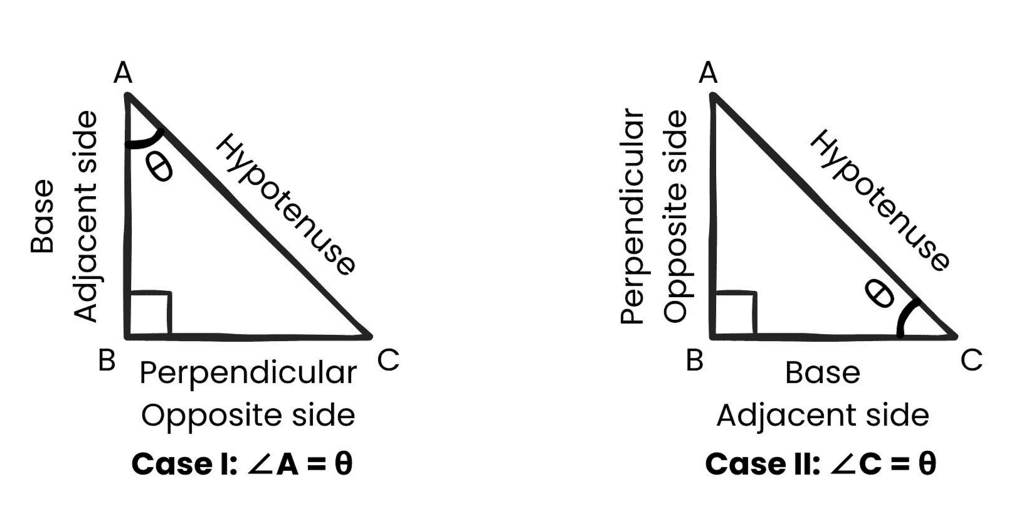
In a right triangle ABC, right-angled at B. Once we have identified the sides, we can define six t-Ratios with respect to the sides.
Note from above six relationships:
- cosecant A = 1/sinA
- secant A = 1/cosineA
- cotangent A = 1/tanA,
However, it is very tedious to write full forms of t-ratios, therefore the abbreviated notations are:
- sine A is sin A
- cosine A is cos A
- tangent A is tan A
- cosecant A is cosec A
- secant A is sec A
- cotangent A is cot A
Example: If in a right-angled triangle ABC, right-angled at B, hypotenuse AC = 5cm, base BC = 3cm and perpendicular AB = 4cm and if ∠ACB = θ, then find tan θ, sin θ and cos θ.
Solution:
Given,
In ∆ABC,
Hypotenuse, AC = 5cm
Base, BC = 3cm
Perpendicular, AB = 4cm
Then,
tan θ = Perpendicular/Base = 4/3
Sin θ = Perpendicular/Hypotenuse = AB/AC = ⅘
Cos θ = Base/Hypotenuse = BC/AC = ⅗
Trigonometric Identities
An equation involving trigonometric ratio of angle(s) is called a trigonometric identity, if it is true for all values of the angles involved. These are: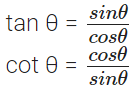
- sin2 θ + cos2 θ = 1 ⇒ sin2 θ = 1 – cos2 θ ⇒ cos2 θ = 1 – sin2 θ
- cosec2 θ – cot2 θ = 1 ⇒ cosec2 θ = 1 + cot2 θ ⇒ cot2 θ = cosec2 θ – 1
- sec2 θ – tan2 θ = 1 ⇒ sec2 θ = 1 + tan2 θ ⇒ tan2 θ = sec2 θ – 1
- sin θ cosec θ = 1 ⇒ cos θ sec θ = 1 ⇒ tan θ cot θ = 1\
Example: Express the ratios cosA, tanA, and secA in terms of sinA.
Solution: Since cos2A + sin2A = 1, therefore:
cos2A = 1 − sin2A
i.e., cosA = ±√1−sin2A
This gives:
cosA = √1 − sin2A
Hence,
and
Note: A trigonometric ratio only depends upon the angle ‘θ’ and stays the same for same angle of different sized right triangles.
Values of Trigonometric Ratios of Specified Angles 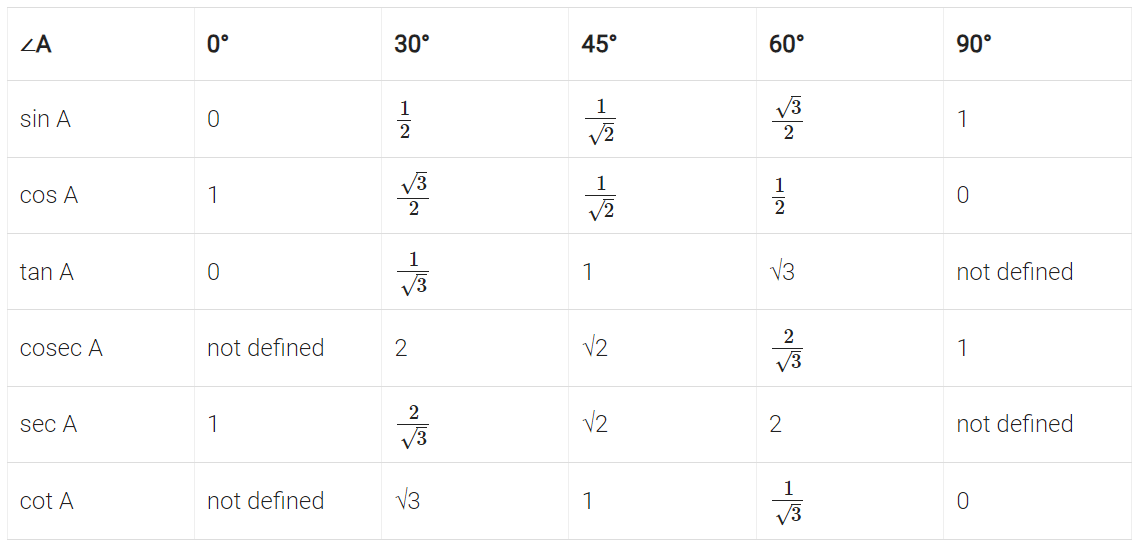
The value of sin θ and cos θ can never exceed 1 (one) as opposite side is 1. Adjacent side can never be greater than hypotenuse since hypotenuse is the longest side in a right-angled ∆.
Example: If tan θ + cot θ = 5, find the value of tan2θ + cotθ.
Solution:
tan θ + cot θ = 5 … [Given
tan2θ + cot2θ + 2 tan θ cot θ = 25 … [Squaring both sides
tan2θ + cot2θ + 2 = 25
∴ tan2θ + cot2θ = 23
Example: If sec 2A = cosec (A – 27°) where 2A is an acute angle, find the measure of ∠A.
Solution:
sec 2A = cosec (A – 27°)
cosec(90° – 2A) = cosec(A – 27°) …[∵ sec θ = cosec (90° – θ)
90° – 2A = A – 27°
90° + 27° = 2A + A
⇒ 3A = 117°
∴ ∠A = 117°/3 = 39°
|
127 videos|584 docs|79 tests
|
FAQs on Introduction to Trigonometry Class 10 Notes Maths Chapter 8
| 1. What are the basic trigonometric ratios and how are they defined? |  |
| 2. What are some important trigonometric identities? |  |
| 3. How is the unit circle related to trigonometry? |  |
| 4. What practical applications do trigonometric ratios have in real life? |  |
| 5. How can one prove trigonometric identities effectively? |  |