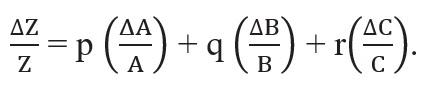Accuracy, Precision of Instruments & Errors in Measurement | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Accuracy and Precision in Measurements |

|
| Errors |

|
| Representation of Errors |

|
| Least Count |

|
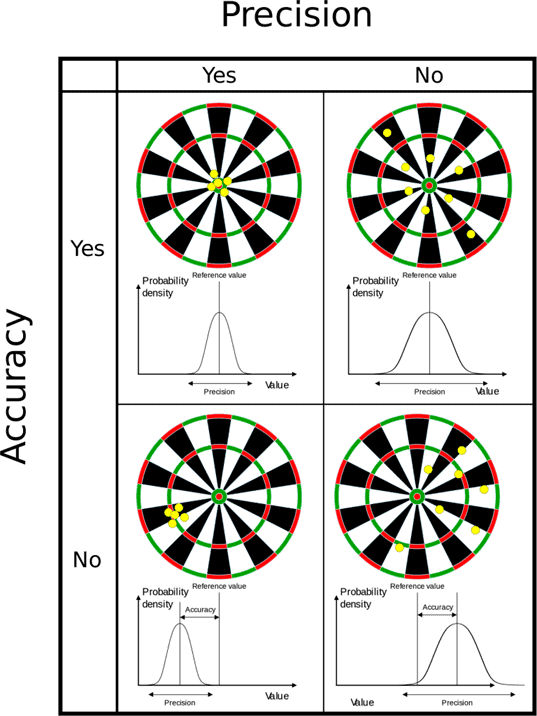
Accuracy and Precision in Measurements
- When we talk about accuracy in measurements, we mean how close a measured value is to the actual value of what we're measuring. For instance, if you weigh a substance in the lab and get 3.2 kg, but the true weight is 10 kg, your measurement is not accurate.
- On the other hand, precision refers to how close two or more measurements are to each other. Using the same example, if you weigh the substance five times and always get 3.2 kg, your measurements are very precise.
- It's important to note that precision is independent of accuracy. This means that measurements can be precise without being accurate, and vice versa. The example below illustrates this concept.
Types of Precision:
- Repeatability: This refers to the differences observed when the same conditions are maintained, and several measurements are taken over a short time frame.
- Reproducibility: This indicates the variation that occurs when using the same measurement method across different tools and operators over a longer period. In simpler terms, accuracy is how close a measurement is to its true value.
- Precision is how much repeated measurements remain consistent under the same conditions.
- An easy way to understand accuracy and precision is to think of a football player aiming for a goal. If the player scores, he is accurate. If he consistently hits the same goalpost, he is precise but not accurate.
- So, a player can be accurate even if his shots are scattered, as long as he scores. A precise player will hit the same spot every time, regardless of whether he scores.
- A player who is both precise and accurate will aim at one target and score a goal.
Errors
The error in measurement refers to the discrepancy between the actual value and the measured value of an object. Errors can arise from various sources and are typically categorized as follows:
Systematic or Controllable Errors
Systematic errors have identifiable causes and can be either positive or negative. Since the causes are understood, these errors can be minimized. Systematic errors are further classified into three types:
- Instrumental errors: These errors occur due to issues like poor design, faulty manufacturing, or improper use of the measuring instrument. They can be mitigated by using more accurate and precise instruments.
- Environmental errors: These errors arise from variations in external conditions such as temperature, pressure, humidity, dust, vibrations, or the presence of magnetic and electrostatic fields.
- Observational errors: These errors occur due to improper setup of the measurement equipment or carelessness in taking measurements.
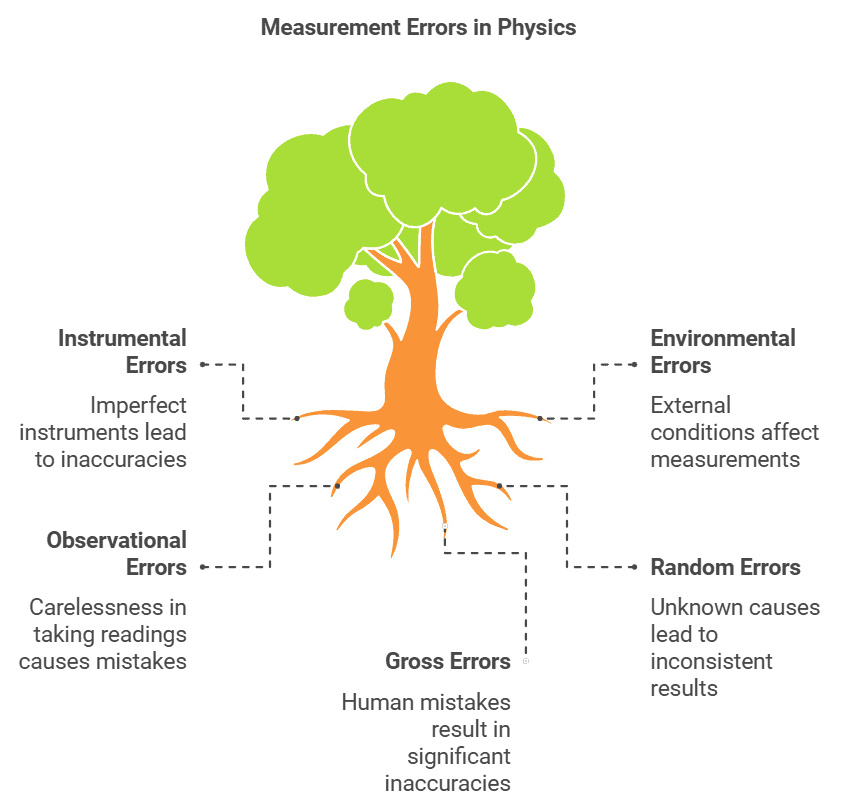
Random Errors
Random errors occur for unknown reasons and happen irregularly, varying in size and sign. While it is impossible to completely eliminate these errors, their impact can be reduced through careful experimental design. For example, when the same person repeats a measurement under identical conditions, they may obtain different results at different times.
- Random errors can be minimized by repeating measurements multiple times and calculating the average of the results. This average is likely to be close to the true value.
Note: When a measurement is taken n times, the random error decreases to (1/n. times.
Example: For instance, if the random error in the average of 100 measurements is x, then the random error in the average of 500 measurements will be x /5.
Gross Errors
Gross errors are caused by human mistakes and carelessness in taking measurements or recording results. Some examples of gross errors include:
- Reading the measurement instrument without the correct initial settings.
- Taking measurements incorrectly without following necessary precautions.
- Making errors in recording the measurements.
- Using incorrect values in calculations.
These errors can be reduced through proper training and by paying careful attention to detail during the measurement process.
Representation of Errors
When we measure something, there can be mistakes or differences between what we measure and the true value. These mistakes are called errors, and they can be shown in different ways.
1. Absolute Error (Δa)
Absolute Error is the difference between the actual value and the measured value of something.
Suppose a physical quantity is measured n times and the measured values are a1, a2, a3 ..........an. The arithmetic mean (am) of these values is
am = 
If the true value of the quantity is not given then mean value (am) can be taken as the true value. Then the absolute errors in the individual measured values are –
Δa1 = am – a1
Δa2 = am – a2
.........
Δan = am – an
The arithmetic mean of all the absolute errors is defined as the final or mean absolute error (Δa)m or  of the value of the physical quantity a
of the value of the physical quantity a 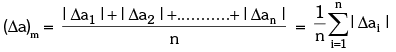
So if the measured value of a quantity be 'a' and the error in measurement be Δa, then the true value (at) can be written as at = a ± Δa
2. Relative or Fractional Error
- Relative Error, also known as Fractional Error, is the ratio of the Mean Absolute Error to either the true value or the mean value of the measured quantity.
- It helps us understand how significant the error is in relation to the size of the measurement.
- For example, if the Mean Absolute Error is 2 cm and the true value is 100 cm, the Relative Error would be 2/100 = 0.02 or 2%.
- When we express Relative Error as a percentage, it becomes Percentage Error. This is calculated by multiplying the Relative Error by 100.
- For instance, if the Relative Error is 0.02, the Percentage Error would be 0.02 × 100 = 2%.
Propagation of Errors in Mathematical Operations
Rule I: When adding or subtracting two quantities, the maximum absolute error in the result is the sum of the absolute errors of each quantity.
- For example, if X = A + B or X = A - B, and ± ΔA and ± ΔB are the absolute errors in A and B respectively, then the maximum absolute error in X is:
- ΔX = ΔA + ΔB
- The result can be expressed as X ± ΔX (in absolute error) or X ± ΔX/X × 100% (in percentage error).
Rule II:
When multiplying or dividing quantities, the maximum fractional or relative error in the result is the sum of the fractional or relative errors of the individual quantities.
- For example, if X = AB or X = A/B, then:

Rule III: The maximum fractional error in a quantity raised to a power (n) is n times the fractional error in the quantity itself, i.e.
If X = An then 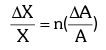
If X = ApBq Cr then 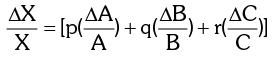
If 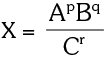 then
then 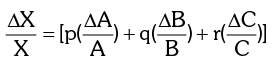
Least Count
The least count (L.C.) refers to the smallest measurement that an instrument can accurately make. It is a crucial aspect of precision measuring devices.
Least Count of Vernier Callipers
Suppose the size of one main scale division (M.S.D.) is M units and that of one vernier scale division (V. S. D.) is V units. Also let the length of 'a' main scale divisions is equal to the length of 'b' vernier scale divisions.
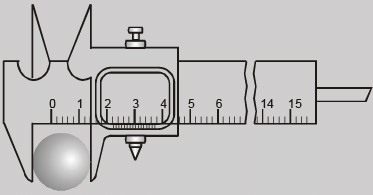
The quantity (M-V) is called vernier constant (V.C) or least count (L.C) of the the vernier callipers.
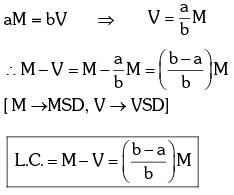
Least Count of screw gauge or spherometer
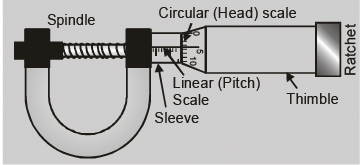
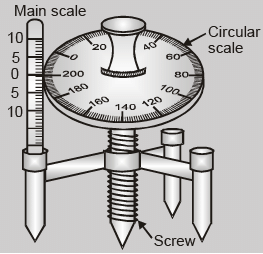
Least Count = Pitch/Total no. of divisions on the circular scale
where pitch is defined as the distance moved by the screw head when the circular scale is given one complete
rotation. i.e. Pitch = Distance moved by the screw on the linear scale/Number of full rotations given
Note: With the decrease in the least count of the measuring instrument, the accuracy of the measurement increases and the error in the measurement decreases.
Types of Errors in Combination
- Error in a Sum or a Difference
- Error in a Product or a Quotient
- Error in a Measured Quantity Raised to a Power
Error of A Sum or A Difference
- Rule: When adding or subtracting two quantities, the total absolute error is the sum of the absolute errors of the individual quantities.
- Explanation:Let two measured quantities be A ± ΔA and B ± ΔB. To find the error ΔZ in the sum Z = A + B, we have:
- Z ± ΔZ = (A ± ΔA) + (B ± ΔB)
- The maximum possible error in Z is ΔZ = ΔA + ΔB.
- For the difference. = A – B, we have:
- Z ± ΔZ = (A ± ΔA) – (B ± ΔB) = (A – B) ± (ΔA + ΔB)
- Thus, the maximum error ΔZ is also ΔA + ΔB.
Error of A Product or A Quotient
- Rule: When multiplying or dividing two quantities, the total relative error is the sum of the relative errors of the factors.
- Explanation: Let Z = AB, with measured values A ± ΔA and B ± ΔB. Then:
- Z ± ΔZ = (A ± ΔA)(B ± ΔB) = AB ± BΔA ± AΔB ± ΔAΔB.
Dividing LHS by Z and RHS by AB we have,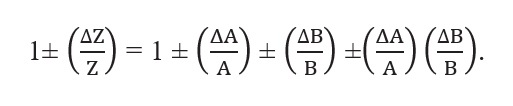
Since ΔA and ΔB are small, we shall ignore their product.
Hence the maximum relative error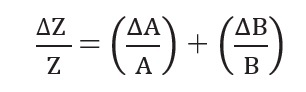
You can easily verify that this is true for division also.
Error in a Measured Quantity Raised to a Power
- Rule: The relative error in a quantity raised to the power k is k times the relative error of the quantity itself.
- Explanation: If Z = A2, then:
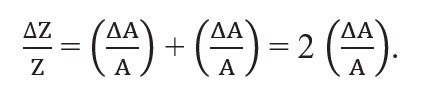
- The relative error in A2 is twice the error in A.
- In general, if
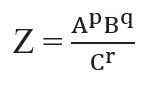 , then:
, then:
|
95 videos|367 docs|98 tests
|
FAQs on Accuracy, Precision of Instruments & Errors in Measurement - Physics Class 11 - NEET
| 1. What is accuracy in measurements? |  |
| 2. What are common types of errors in measurements? |  |
| 3. How is the least count of an instrument defined? |  |
| 4. What is the difference between accuracy and precision in measurements? |  |
| 5. How can errors in measurement be minimized? |  |