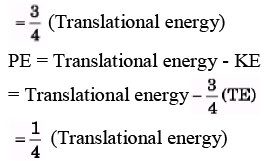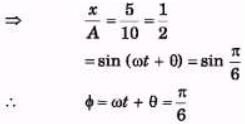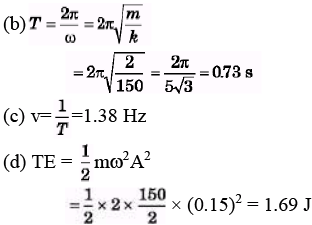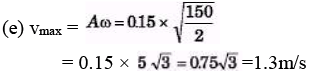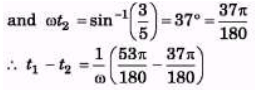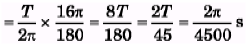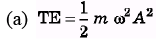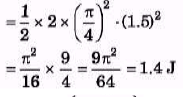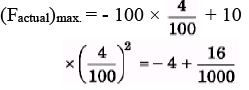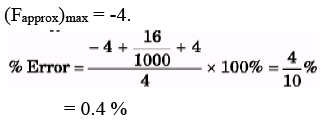DC Pandey Solutions: Simple Harmonic Motion - 1 | Physics Class 11 - NEET PDF Download
Introductory Exercise 11.1
Q.1. A particle moves under the force F(x) = (x2 - 6x) N, where x is in metres. For small displacements from the origin, what is the force constant in the simple harmonic motion approximation?
Sol.
F(x)=x2 -6x
Fr = F(x+ Δx) - F(x)
= (x + Δ)2 - 6(x+ Δx) - x2 + 6x
= 2xΔx - 6Δx = -(6 - 2x) Δx
= - 6Δx for x = 0
kΔx ⇒ k = 6N/m
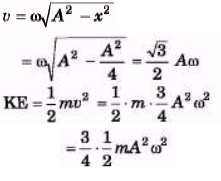
Q.2. At A= A/2, what fraction of the mechanical energy is potential? What fraction is kinetic? Assume potential energy to be zero at the mean position.
Sol.
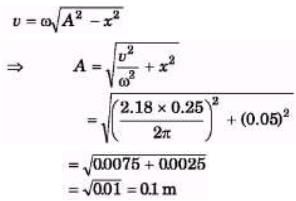
Q.3. The initial position and velocity of a body moving in SHM with period T = 0.25 s are x = 5.0 cm and v = 218 cm/s. What are the amplitude and phase constant of the motion?
Sol.
= 10cm
x = A sin (ωt + θ)
Q.4. A cart of mass 2.00 kg is attached to the end of a horizontal spring with force constant k = 150 N/m. The cart is displaced 15.0 cm from its equilibrium position and released. What are (a) the amplitude (b) the period (c) the frequency (d) the mechanical energy (e) the maximum velocity of the cart? Neglect friction.
Sol.
(a) Maximum displacement
= 15 cm = Amplitude.
Q.5. A body of mass 0.10 kg is attached to a vertical massless spring with force constant 4.0 x 10" N/m. The body is displaced 10.0 cm from its equilibrium position and released. How much time elapses as the body moves from a point 8,0 cm on one side of the equilibrium position to a point 6.0 cm on the same side of the equilibrium position?
Sol.
A = 10cm
8 cm = 10 sin ωt1 and 6 cm = 10 sin ωt2
= 1.4 × 10-3s
Q.6. Does a 2.0 kg particle undergo SHM according to x = 1.5 sin 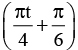 (in SI units
(in SI units
(a) What is the total mechanical energy of the particle?
(b) What is the shortest time required for the particle to move from x = 0.5 m to x = - 0.75 m?
Sol.
Q.7. A body of mass 200 g is in equilibrium at x = 0 under the influence of a force F(x) = (-100x + 10x2) N
(a) If the body is displaced a small distance from equilibrium, what is the period of its oscillations?
(b) If the amplitude is 4.0 cm, by how much do we error in assuming that F(x) = - kx at the end points of the motion.
Sol.
|
122 videos|493 docs|98 tests
|
FAQs on DC Pandey Solutions: Simple Harmonic Motion - 1 - Physics Class 11 - NEET
| 1. What is simple harmonic motion? |  |
| 2. What are the characteristics of an object in simple harmonic motion? |  |
| 3. How is the period of simple harmonic motion related to its frequency? |  |
| 4. What is the relationship between the amplitude and energy of an object in simple harmonic motion? |  |
| 5. How does damping affect simple harmonic motion? |  |