Solved Examples: Work, Energy & Power | Physics Class 11 - NEET PDF Download
Some solved Examples
Ex.1 Two blocks each of mass M are connected to the ends of a light frame as shown in figure. The frame is rotated about the vertical line of symetry. The rod breaks if the tension in it exceeds T0. Find the maximum frequency with which the frame may be rotated without breaking the rod.
Sol. Consider one of the blocks. If the frequency of revolution is f, the angular velocity is w = 2pf. The acceleration towards the centre is w2l = 4 p2 f2 l . The only horizontal force on the block is the tension of the rod. At the point of breaking, this force is T0. So from Newton's law,
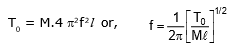
Ex.2 Prove that a motor car moving over a convex bridge is lighter than the same car resting on the same bridge.
Sol. The motion of the motor car over a convex bridge AB is the motion along the segment of a circle AB (figure);
The centripetal force is provided by the difference of weight mg of the car and the normal reaction R of the bridge.
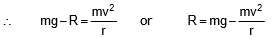
Clearly R < mg, i.e., the weight of the moving car is less than the weight of the stationary car.
Ex.3 A body weighing 0.4 kg is whirled in a vertical circle with a string making 2 revolutions per second. If the radius of the circle is 1.2m. Find the tension (a) at the top of the circle, (b) at the bottom of the circle. Give : g = 10 m s-2 and p = 3.14
Sol. Mass, m = 0.4 kg ;
time period = second, radius, r = 1.2 m
Angular velocity, w = = 4p rad s-1 = 12.56 rad s-1
(a) At the top of the circle, T = -mg
= mrw2 -mg = m (rw2 -g)
= 0.4 (1.2 × 12.56 × 12.56 -9.8) N = 71.2 N
(b) At the lowest point, T = m(rw2 + g) = 80 N
Ex.4 A metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of ring moves with velocity v. Find the tension in the ring.
Sol. Consider a small part ACB of the ring that subtends an angle Dq at the centre as shown in figure.
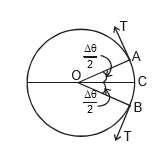
Let the tension in the ring be T.
The forces on this elementary portion ACB are
(i) tension T by the part of the ring left to A
(ii) tension T by the part of the ring to B
(iii) weight (Dm) g
(iv) nomal force N by the table.
As the elementary portion ACB moves in a circle of radius R at constant speed v its acceleration towards centre is
Length of the part ACB = RA8. The mass per unit length of the ring is
mass of this portion ACB,
Putting this value of Δm in (ii),
Since AS is small So is equal to 1,
Ex.5 A small smooth ring of mass m is threaded on a light inextensible string of length 8L which has its ends fixed at points in the same vertical line at a distance 4L apart. The ring describes horizontal circles at constant speed with both parts of the string taut and with the lower portion of the string horizontal. Find the speed of the ring and the tension in the string. The ring is then tied at the midpoint of the string and made to perform horizontal circles at constant speed of . Find the tension in each part of the string.
Sol. When the string passes through the ring, the tension in the string is the same in both parts. Also from geometry
BP = 3L and AP = 5L
T cosq = T = mg ...(i)
In the second case, ABP is an equilateral triangle.
Solving equation (iii) and (iv)
Ex.6 A large mass M and a small mass m hang at the two ends of the string that passes through a smooth tube as shown in Figure. The mass m moves around in a circular path, which lies in the horizontal plane. The length of the string from the mass m to the top of the tube is l and q is the angle this length makes with vertical. What should be the frequency of rotation of mass m so that M remains stationary ?
Sol.

The forces acting on mass m and M are shown in Figure. When mass M is stationary
T = Mg ..(i)
where T is tension in string.
For the smaller mass, the vertical component of tension T cos q balances mg and the horizontal component T sin q supplies the necessary centripetal force.
|
95 videos|367 docs|98 tests
|

















