Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Solving Trig Equations
Solving Trig Equations | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Solving Trig Equations
- You can use the symmetry of trigonometric graphs to find multiple solutions to a trigonometric equation.
How are trigonometric equations of the form sin x = k solved?
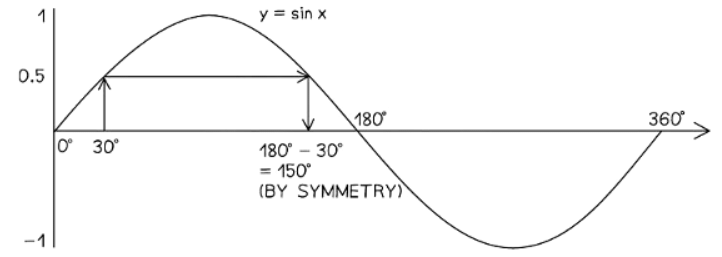
- The equation sinx = 0.5 yields solutions in the range 0° < x < 360°, which are x = 30° and x = 150°.
- To confirm, one can check on a calculator that both sin(30°) and sin(150°) result in 0.5.
- The first solution is obtained by taking the inverse sine of 0.5, resulting in x = sin−1(0.5) = 30°.
- The second solution stems from the graph's symmetry of y = sinx between 0° and 360°.
- Sketch the graph and draw a vertical line from x = 30° to the curve, then horizontally across to another point on the curve, and finally vertically back to the x-axis.
- Due to the curve's symmetry, the new value of x is 180° − 30° = 150°.
- Generally, if x° is an acute angle solving sinx = k, then 180° − x° is the obtuse angle solving the same equation.
- If the calculator presents x as a negative value, continue drawing the curve to the left of the x-axis to aid visualization.
How are trigonometric equations of the form cos x = k solved?
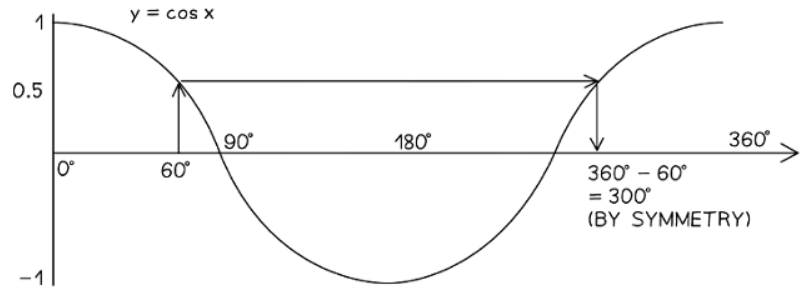
- In the range 0° < x < 360°, the solutions to the equation cosx = 0.5 are x = 60° and x = 300°.
- To confirm, one can verify on a calculator that both cos(60°) and cos(300°) yield 0.5.
- The first solution is obtained by taking the inverse cosine of 0.5, resulting in x = cos−1(0.5) = 60°.
- The second solution arises from the graph's symmetry of y = cosx between 0° and 360°.
- Sketch the graph and draw a vertical line from x = 60° to the curve, then horizontally across to another point on the curve, and finally vertically back to the x-axis.
- Due to the curve's symmetry, the new value of x is 360° − 60° = 300°.
- Generally, if x° is an angle solving cosx = k, then 360° − x° is another angle solving the same equation.
- If the calculator displays x as a negative value, continue drawing the curve to the left of the x-axis to facilitate understanding.
How are trigonometric equations of the form tan x = k solved?
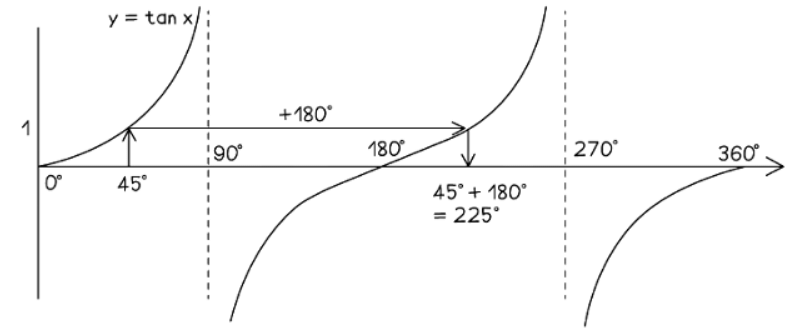
- The equation tan x = 1 yields solutions of x = 45° and x = 225° within the range of 0° to 360°.
- Confirming these solutions on a calculator, both tan(45°) and tan(225°) result in 1.
- The first solution, x = 45°, is directly obtained by taking the inverse tangent of both sides: x = tan⁻¹(1).
- The second solution, x = 225°, arises from the symmetry of the tangent graph within the range of 0° to 360°.
- To illustrate this symmetry, sketch the graph of y = tan x.
- Draw a vertical line from x = 45° to intersect the curve, then extend it horizontally to another point on the curve, representing a different "branch" of tan x.
- Extend a vertical line from this point back to the x-axis.
- This new x-value is found by adding 180° to the initial x-value: 45° + 180° = 225°.
- In general, for any angle x° that solves the equation tan x = k, adding 180° yields another solution.
- If the calculator provides a negative value for x, continuing to draw the curve to the left of the x-axis can assist in visualizing the symmetry.
The document Solving Trig Equations | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
42 videos|395 docs|19 tests
|
FAQs on Solving Trig Equations - Mathematics for GCSE/IGCSE - Class 10
| 1. How do you solve trigonometric equations of the form tan x = k? |  |
Ans. To solve trigonometric equations of the form tan x = k, you can use the inverse trigonometric function arctan. Simply take the arctan of both sides of the equation to find the value of x.
| 2. What should you do if the value of k in the equation tan x = k is outside the range of the arctan function? |  |
Ans. If the value of k is outside the range of the arctan function, you can use the periodicity of the tan function to find all possible solutions. Remember that tan(x) has a period of π, so you can add or subtract multiples of π to the arctan value to find all solutions.
| 3. Can you use a calculator to solve trigonometric equations involving tan x = k? |  |
Ans. Yes, you can use a calculator to solve trigonometric equations involving tan x = k. Simply input the value of k and use the arctan function on your calculator to find the solution for x. Make sure to check if your calculator is set to the correct angle mode (degrees or radians).
| 4. Are there any restrictions on the values of x when solving trigonometric equations? |  |
Ans. When solving trigonometric equations, you should consider any restrictions on the values of x. For example, if the equation involves a denominator, make sure that the denominator is not equal to zero, as this would result in an undefined value. Additionally, some equations may have restrictions based on the domain of the trigonometric function.
| 5. How can you check your solutions to trigonometric equations? |  |
Ans. To check your solutions to trigonometric equations, substitute the values of x back into the original equation and verify if both sides are equal. You can also graph the trigonometric functions involved and see if the points of intersection correspond to your solutions.
Related Searches




















