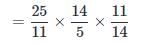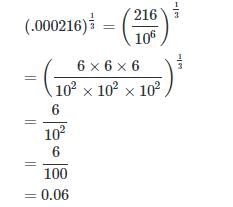All Courses
Get the App Signup / Login
Sign in Open App
CLAT Exam  >  CLAT Notes  >  Quantitative Techniques for CLAT  >  Squares, Square Roots, Cubes, Cube Roots

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT PDF Download

Understanding the concepts of squares, square roots, cubes, and cube roots is crucial for various mathematical problems, and it's a fundamental aspect of quantitative aptitude tested in exams like CLAT (Common Law Admission Test).

SQUARES, SQUARE ROOTS, CUBES, CUBE ROOTS

Squares: When the exponent of a base is 2, the numbers obtained are called squares or squared numbers.

Perfect Square: A  natural number is called a perfect square if it is the square of a number.

1, 4, 9, 16, 25, 36 --------- are the perfect square of the numbers

1, 2, 3, 4, 5, 6 ------------ respectively.

5, 6, 7, 8, 11, 50, and 125 are not perfect squares of any natural number.

Examples of Perfect SquareExamples of Perfect Square

To determine whether a given number is a perfect square.

Step I: Express the given number as the product of its prime numbers.

Step II: Express the prime factors as pairs of same number

Step III: Check if there are any unpaired factors

Step IV: If there is no unpaired factor, the given number is a perfect square.

 Properties of Squares

1) Squares of even numbers are even.

2) Squares of odd numbers are odd.

3) A number ending with 2, 3, 7, or 8 is never a perfect square. e.g. 23, 347, 2818  cannot be perfect squares.

4) A number ending with an odd number of zeros is never a perfect square. Thus 150, 4400000, and 48000 cannot be perfect squares.

5) The square of a natural number (other than 1) is either a multiple of 3 or exceeds a multiple of 3 by 1.

6) The square of a natural number (other than 1) is either a multiple of 4 or exceeds a multiple of 4 by 1

7) The difference between the squares of two consecutive natural numbers is equal to their sum.

For example: 22 - 12 = 4 – 1 = 3    which is equal to 2 + 1 = 3

52 - 42 = 25 – 16 = 9 which is equal to 5 + 4 = 9

112 - 102 = 121 – 100 = 21 which is equal to 11 + 10 = 21

Example :- Which of the following is not a perfect square in the options given below?

A. 25

B. 89

C. 100

D. 49

Ans: B) 89

Question for Squares, Square Roots, Cubes, Cube Roots
Try yourself:The least perfect square, which is divisible by each of 21, 36 and 66 is:
View Solution

Some interesting facts:

1) Pythagorean Triplets: For every natural number m (other than 1) there is a triplet such as (2m), (m2-1), and (m2+1)

These triplets are called Pythagorean Triplets. They obey the relation (2m)2+(m2-1)2=(m2+1)2

For m = 2, Pythagorean triplets are 2 x 2, 22-1, 22+1 or 4, 3 and 5 and (4)2 + (3)2 = 52

For m = 4, triplets are 4 x 2,  42 - 1, 42 + 1

i.e. 8, 15, 17 and 82 + 152 = 172

and so on it is true for every natural number.

2) The square of any natural number will have either 0, 1, 4, 5, 6, or 9 at the unit place.

3) The square of a natural number (n) is always equal to the sum of the first (n) odd natural numbers.

If x = 4 Then 42 = 1 + 3 + 5 + 7

If x = 6 Then 62 = 1 + 3 + 5 + 7 + 9 + 11

If x = 9 Then 92 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17

4) If n is a perfect square then 2n can never be a perfect square.

5) A perfect square number is never negative.

Square Roots

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT


The square root of a number n is that number which when multiplied by itself gives n as the product. For example 7 x 7 = 49, So 7 is the square root of 49. It is written as Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Finding the square root of a perfect square

(a) By finding prime factors 

Example 1: If the square root of 576 is to be found out we find the prime factors of 576?

Solution: 576 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Make pairs of factors and pick up one factor from each pair.

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT = 2 x 2 x 2 x 3 = 24 

Example 2: Simplify  Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT


Solution: 900 = 30 x 30    Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

0.09 = 0.3 x 0.3  Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT = 0.3

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT0.003

= 30.303

(b) Finding the square root by long division method


Example 1: Find the square root of 7396

Solution:

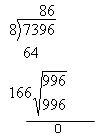
Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT 

Step I: Beginning from the right, reduce the digits in pairs from right to left.

Step II: Take the first pair of digits and find the nearest sq. root. The nearest square root of 73 is 8. Write 8 as quotient and also as divisor. Write the product 8 x 8 = 6 below 73 and Subtract.

The remainder is 9

Step III: Bring down the next pair 96. Double 8, the number in the quotient and place the double i.e. 16 as the next divisor. Now 99 divided by 16 is approximately 6. So put 6 with 8 in the quotient also with 16 as the divisor and multiply 166 by 6 and get 996. Now the remainder is zero. So 86 is the exact square root.

Therefore Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Example 2: Find the sq. root of Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Solution:Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Finding the number of digits in the square root of a perfect square. 

Rule

If a perfect square contains n digits then, its square root will contain Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT digits if n is even and Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT digits if n is odd.

Question for Squares, Square Roots, Cubes, Cube Roots
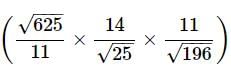Try yourself:Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLATis equal to 
View Solution

Finding the Square Root of a Perfect Square Decimal Number by Long Division.

While finding the square root of a natural number we make pairs from right to left and if in the last, one digit is left, we leave it by itself. In case of decimal number we make pairs from right to left for the integral part and from left to right for the decimal portion.

If the last period of the decimal number contains only one digit, we add zero to it. The square root of a decimal number will contain as many decimal places as there are pairs in the decimal part of the given number. The method to be followed is the same as for the whole number.

Example 1: If Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT = 56. Find the value of Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT + Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Solution: Since Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT = 56

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT = 5.6

  and Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT = 0.56

∴ Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT + Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT .= 5.6 + 0.56 = 6.16

Example 2: Find the value of

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

If Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

 Solution:

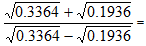
Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT 

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Example 3: Evaluate Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Solution: Given expression = Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Example 4: Evaluate Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Solution: The sum of decimal places both in the numerator as well as denominator is 6. So we can remove the decimals

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Example 7: Find the least number which must be added to 4562 to make it a perfect square.


Solution:

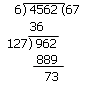
   Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT                                                

8 x 128 = 1024

If in place of 962 it is 1024 we will get a perfect square so add

1024 – 962 = 62

Cubes

A cube of a number, is that number raised to the power 3. The cube of a number is obtained by multiplying it with itself 3 times.

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Cube of 5 is 5 x 5 x 5 = 125

Cube of 6 is 6 x 6 x 6 = 216

How to determine whether a given number is a perfect cube

Step 1: Make prime factors of the given number

Step 2: Make groups of the prime factors – a group containing 3 same numbers.

Step 3: Check the ungrouped factor

Step 4: If there is no ungrouped factor, the number is a perfect cube.

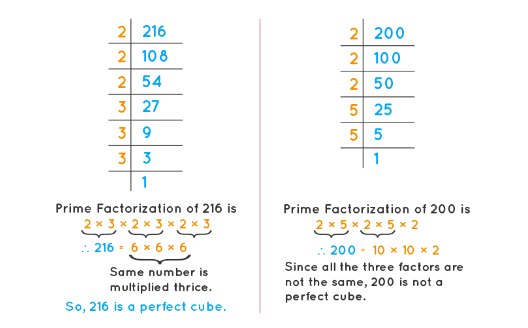Perfect Cube ExamplePerfect Cube Example

Example: Is 1728 a perfect cube

Solution: Prime factors of 1728 are = 2 x 2 x 2  x  2 x 2 x 2  x  3 x 3 x 3

The prime factors can clearly be grouped into groups of 3 each and no factor is left ungrouped

So 1728 is a perfect cube.

Properties of cubes:

(i) Cube of a natural number is a natural number

(ii) Cube of all even natural numbers are even.

(iii) Cube of all odd natural numbers are odd.

(iv) Cubes of all negative numbers are negative.

(v) For any rational number Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT 

(vi) Cube of a natural number, which is a multiple of 3, is a multiple of 27

(vii) Cube of a natural number of the form 3n+1 is also a natural number of the form 3n+1

(viii) Cube of a natural number of the form 3n+2 is also a natural number of the form 3n+2

(ix) Cube of a number, having a zero at the unit place, has three zeros at the end.

For example (10)3 = 1000

Example: What is the smallest number by which 2400 be multiplied so that the product is a perfect cube?

a) 70     b) 80     c) 90     d) 60

Solution: 2400 = 2 x 2 x 2  x 2 x 2 x 3 x 5 x 5

After making the groups of three for each prime number we need one 2’s, two 3’s and one 5.

So we need a number 2 x 3 x 3 x 5 i.e. 90

So option (c) is correct.

Cube roots

A natural number n is a cube root of the number m if m = n3

The symbol for cube root is Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

To find the cube root of a perfect cube number

Step 1: Make prime factors of the given number

Step 2: Make groups of three each of the prime factors

Step 3: Choose one out of the group of three factors and find their product

Step 4: This product is the required cube root of the given number.

Example: Find the cube root of -4096

Solution: Prime factors of 4096 are 2 x 2 x 2  x  2 x 2 x 2  x  2 x 2 x 2  x  2 x 2 x 2

Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT

Question for Squares, Square Roots, Cubes, Cube Roots
Try yourself:The cube root of .000216 is:
View Solution

The document Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT is a part of the CLAT Course Quantitative Techniques for CLAT.
All you need of CLAT at this link: CLAT
57 videos|108 docs|73 tests
Join Course for Free

Top Courses for CLAT

FAQs on Squares, Square Roots, Cubes, Cube Roots - Quantitative Techniques for CLAT

1. How do I determine whether a given number is a perfect square?
Ans. To determine whether a number is a perfect square, you can take the square root of the number and check if it is an integer. If the square root is an integer, then the number is a perfect square. For example, if you want to determine whether 25 is a perfect square, you can take the square root of 25, which is 5. Since 5 is an integer, 25 is a perfect square.
2. How can I find the square root of a perfect square?
Ans. To find the square root of a perfect square, you can simply take the square root of the number. For example, if you want to find the square root of 81, you can take the square root of 81, which is 9. So, the square root of 81 is 9.
3. How can I find the number of digits in the square root of a perfect square?
Ans. To find the number of digits in the square root of a perfect square, you can count the number of digits in the original number and divide it by 2. If the original number has an odd number of digits, round up the result. If the original number has an even number of digits, round down the result. For example, if the original number is 100, it has 3 digits. Dividing 3 by 2 gives 1.5, so the square root of 100 has 2 digits.
4. How can I find the square root of a perfect square decimal number by long division?
Ans. To find the square root of a perfect square decimal number by long division, you can follow these steps: 1. Group the digits in pairs from right to left, starting from the decimal point. 2. Find the largest integer whose square is less than or equal to the leftmost group of digits. Write this integer as the leftmost digit of the square root. 3. Subtract the square of this integer from the leftmost group of digits and bring down the next pair of digits. 4. Double the leftmost digit of the square root and find the largest digit to be placed as the next digit in the square root, such that when this digit is multiplied by the doubled leftmost digit and placed as the next digit in the square root, the resulting number is less than or equal to the number obtained by bringing down the next pair of digits. 5. Repeat steps 3 and 4 until all the digits have been brought down. For example, to find the square root of 2.25, you can follow these steps and find that the square root is 1.5.
5. How can I determine whether a given number is a perfect cube?
Ans. To determine whether a number is a perfect cube, you can take the cube root of the number and check if it is an integer. If the cube root is an integer, then the number is a perfect cube. For example, if you want to determine whether 8 is a perfect cube, you can take the cube root of 8, which is 2. Since 2 is an integer, 8 is a perfect cube.
Related Exams
About this Document
4.5K Views
4.85/5 Rating
Dec 22, 2024 Last updated
Document Description: Squares, Square Roots, Cubes, Cube Roots for CLAT 2024 is part of Quantitative Techniques for CLAT preparation. The notes and questions for Squares, Square Roots, Cubes, Cube Roots have been prepared according to the CLAT exam syllabus. Information about Squares, Square Roots, Cubes, Cube Roots covers topics like SQUARES, SQUARE ROOTS, CUBES, CUBE ROOTS, To determine whether a given number is a perfect square.,  Properties of Squares, Some interesting facts:, Square Roots, Finding the square root of a perfect square, Finding the number of digits in the square root of a perfect square. , Finding the Square Root of a Perfect Square Decimal Number by Long Division., Cubes, How to determine whether a given number is a perfect cube, Properties of cubes:, Cube roots and Squares, Square Roots, Cubes, Cube Roots Example, for CLAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Squares, Square Roots, Cubes, Cube Roots.
Introduction of Squares, Square Roots, Cubes, Cube Roots in English is available as part of our Quantitative Techniques for CLAT for CLAT & Squares, Square Roots, Cubes, Cube Roots in Hindi for Quantitative Techniques for CLAT course. Download more important topics related with notes, lectures and mock test series for CLAT Exam by signing up for free. CLAT: Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT
Description
Full syllabus notes, lecture & questions for Squares, Square Roots, Cubes, Cube Roots | Quantitative Techniques for CLAT - CLAT | Plus excerises question with solution to help you revise complete syllabus for Quantitative Techniques for CLAT | Best notes, free PDF download
Information about Squares, Square Roots, Cubes, Cube Roots
In this doc you can find the meaning of Squares, Square Roots, Cubes, Cube Roots defined & explained in the simplest way possible. Besides explaining types of Squares, Square Roots, Cubes, Cube Roots theory, EduRev gives you an ample number of questions to practice Squares, Square Roots, Cubes, Cube Roots tests, examples and also practice CLAT tests
57 videos|108 docs|73 tests
Join Course for Free
Download as PDF
Explore Courses for CLAT exam

Top Courses for CLAT

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

Summary

,

Free

,

Square Roots

,

Cubes

,

video lectures

,

Extra Questions

,

Square Roots

,

Cubes

,

Squares

,

practice quizzes

,

Squares

,

mock tests for examination

,

shortcuts and tricks

,

Square Roots

,

Cube Roots | Quantitative Techniques for CLAT

,

Cube Roots | Quantitative Techniques for CLAT

,

Cube Roots | Quantitative Techniques for CLAT

,

Sample Paper

,

Exam

,

Semester Notes

,

Objective type Questions

,

Previous Year Questions with Solutions

,

MCQs

,

ppt

,

pdf

,

Cubes

,

past year papers

,

Important questions

,

Squares

,

study material

,

Viva Questions

;
Additional Information about Squares, Square Roots, Cubes, Cube Roots for CLAT Preparation

Squares, Square Roots, Cubes, Cube Roots Free PDF Download

The Squares, Square Roots, Cubes, Cube Roots is an invaluable resource that delves deep into the core of the CLAT exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Squares, Square Roots, Cubes, Cube Roots now and kickstart your journey towards success in the CLAT exam.

Importance of Squares, Square Roots, Cubes, Cube Roots

The importance of Squares, Square Roots, Cubes, Cube Roots cannot be overstated, especially for CLAT aspirants. This document holds the key to success in the CLAT exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Squares, Square Roots, Cubes, Cube Roots Notes

Squares, Square Roots, Cubes, Cube Roots Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Squares, Square Roots, Cubes, Cube Roots. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Squares, Square Roots, Cubes, Cube Roots Notes on EduRev are your ultimate resource for success.

Squares, Square Roots, Cubes, Cube Roots CLAT Questions

The "Squares, Square Roots, Cubes, Cube Roots CLAT Questions" guide is a valuable resource for all aspiring students preparing for the CLAT exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Squares, Square Roots, Cubes, Cube Roots on the App

Students of CLAT can study Squares, Square Roots, Cubes, Cube Roots alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Squares, Square Roots, Cubes, Cube Roots, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Squares, Square Roots, Cubes, Cube Roots is prepared as per the latest CLAT syllabus.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup