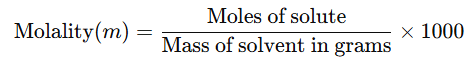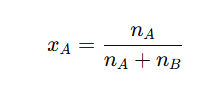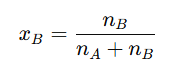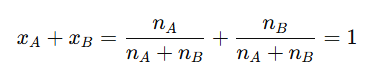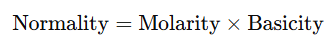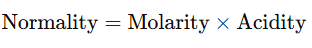Stoichiometry & Concentration Terms | Chemistry Class 11 - NEET PDF Download
| Table of contents |

|
| What is Stoichiometry ? |

|
| Stoichiometric Coefficient |

|
| Mole Concept and Molar Relationships |

|
| Stoichiometric Calculations |

|
| Limiting Reagent |

|
| Reactions in Solutions |

|
What is Stoichiometry ?
Stoichiometry refers to the quantitative relationships between reactants and products in a chemical reaction. The term comes from the Greek words "stoicheion" (meaning element) and "metron" (meaning measure).

It relies on the idea that the stoichiometric coefficients in a chemical equation represent the number of moles of each reactant or product involved.
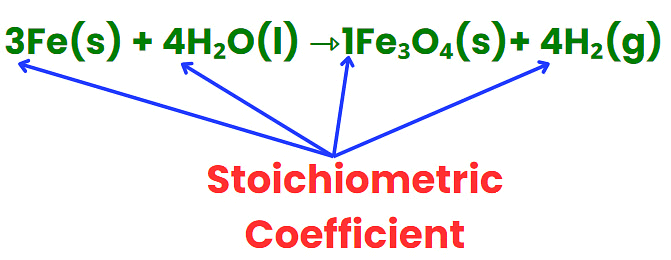
Stoichiometric Coefficient
- It represents the number of molecules involved in a reaction.
- Found in front of atoms, molecules, or ions in a balanced equation.
- Ensures that the number of elements on both sides of the equation is equal.

- Can be whole numbers or fractions.
- Helps establish the mole ratio between reactants and products.
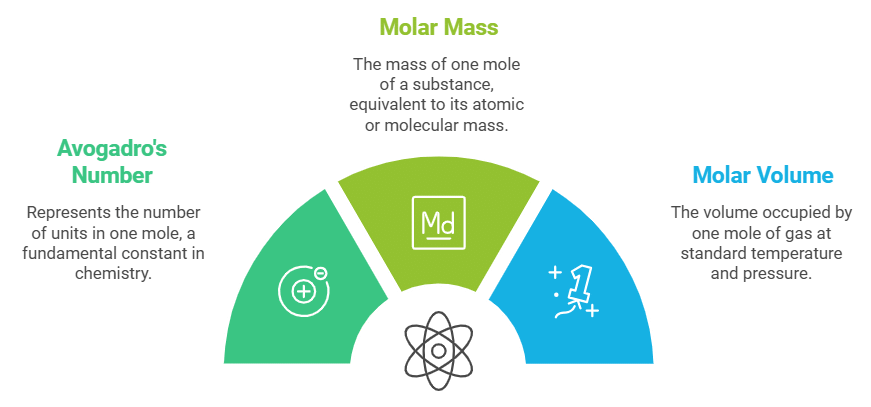
Mole Concept and Molar Relationships
- Atoms and molecules are very small, so large numbers are used to represent them.
- The mole concept is used to express atoms/molecules in bulk.
- 1 mole of any substance contains 6.022 x 10²³ units (Avogadro’s number).
- The molar mass (in grams) of 1 mole is equal to its atomic or molecular mass.
- In reactions involving gases, molar volume is considered.
- For Example : 1 mole of gas occupies 22.4 litres at standard temperature and pressure (STP).

Stoichiometric Calculations
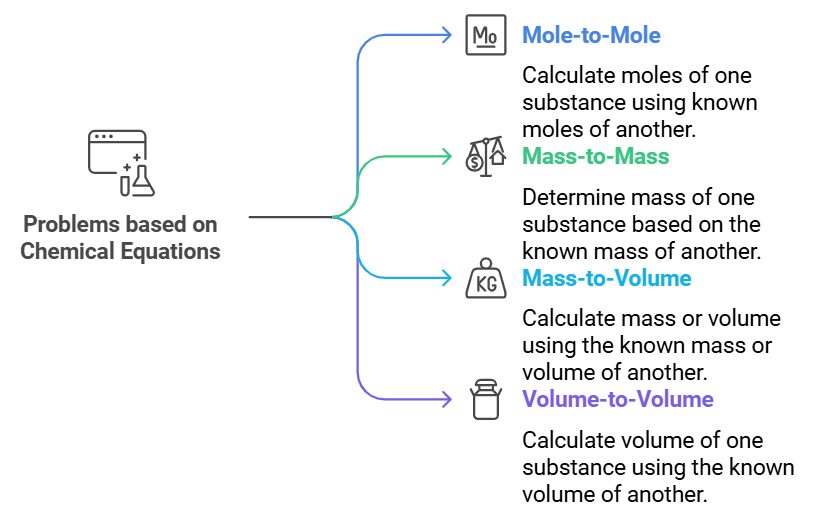
Problems Based on Chemical Equations (Stoichiometry)
Stoichiometric problems based on chemical equations can be divided into the following types:
- Mole-to-mole relationships: These problems involve calculating the moles of one reactant or product when the moles of another are known.
- Mass-to-mass relationships: In this type, the mass of one reactant or product is calculated based on the known mass of another.
- Mass-to-volume relationships: Here, the mass or volume of a reactant or product is calculated using the mass or volume of another substance.
- Volume-to-volume relationships: These problems focus on calculating the volume of one reactant or product when the volume of another is provided.

Steps to solve such problems:
1. Write the balanced chemical equation.
2. Record the moles or gram atomic/molecular masses of the given substances. If there are multiple atoms or molecules involved, multiply the atomic or molecular mass by the number of atoms or molecules.
3. Note down the actual quantities of the given substances. For substances whose weights or volumes need to be calculated, use a question mark (?) as a placeholder.
4. Use the unitary method to calculate the result.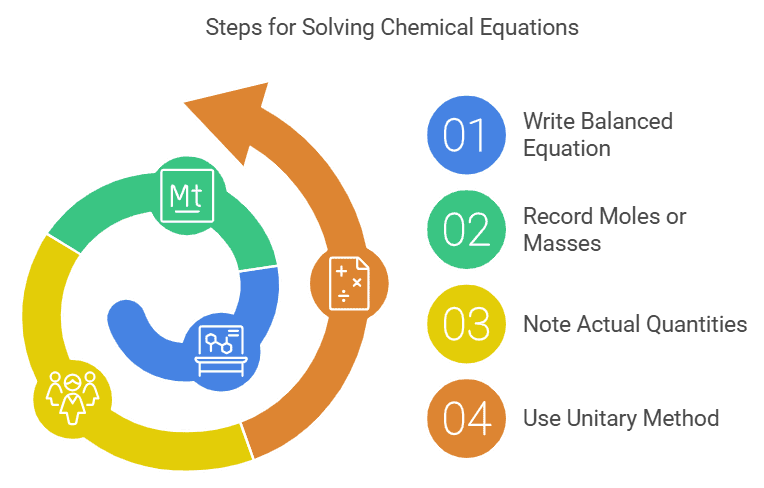
This method can be further explained with examples:
Type I: Mole to Mole Relationship
Example: How many moles of nitrogen are needed to produce 8.2 moles of ammonia by reaction with hydrogen?
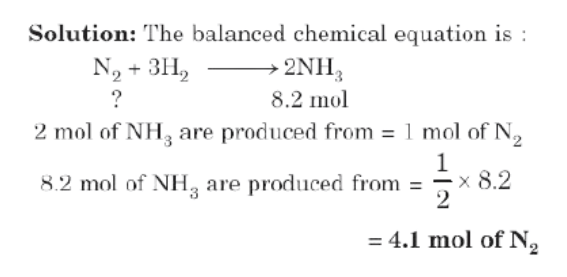
Type II: Mole to Mass or Mass to Mole Relationship
Example: How many moles of methane are required to produce 22g of CO2(g) after combustions?
Type III: Mass - Volume Relationship
Example: Calculate the amount of KCLO3 needed to supply sufficient oxygen for burning 112L of CO gas at N.T.P.
 Type IV: Volume - Volume Relationship
Type IV: Volume - Volume Relationship
Example: Calculate the volume of oxygen at N.T.P. that would be required to convert 5.2L of carbon monoxide to carbon dioxide.

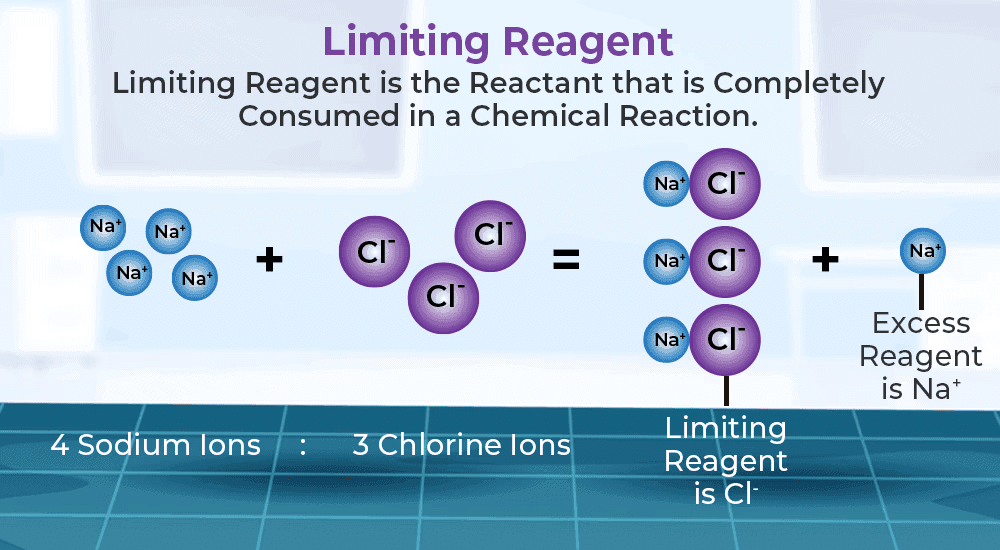
Limiting Reagent
It refers to reactant which is present in minimum stoichiometry quantity for a chemical reaction and gets totally consumed .
- Role in Reaction: It limits the amount of product formed, as the reaction stops once the limiting reagent is used up.
- Determination of Limiting Reagent: In a reaction with multiple reactants, the reagent present in the smallest stoichiometric amount relative to the reaction’s requirements is the limiting reagent.
- Example Reaction: aA + bB → products
- If A is in a smaller stoichiometric amount than B, then A is the limiting reagent.
- Significance: Helps in calculating the theoretical yield of a product, as only the amount of the limiting reagent determines the maximum possible product formation.

Reactions in Solutions
Many reactions occur in solutions. In a solution, the component present in a smaller amount is called the solute, while the one present in a larger amount is the solvent. The concentration of a solution refers to the quantity of solute present in a given amount of solvent or solution.
Concentration can be expressed in several ways, including:
1. Mass Percentage or Volume Percentage
The mass percentage of a component in a solution is defined as the mass of the component per 100g of the solution.
For example, if WA is the mass of component A and WB is the mass of component B in a solution, the mass percentage of A is:
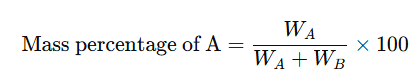
This can be written as w/w. For instance, a 10% (w/w) sodium chloride solution means that 10g of sodium chloride is present in 90g of water, making a total of 100g of solution.
Example: If 11 g of oxalic acid are dissolved in 500 mL of solution (density = 1.1 g mL⁻¹), what is the mass % of oxalic acid in solution?

2. Volume Percentage
The volume percentage is defined as the volume of the component per 100 parts by volume of the solution.
For example, if VA and VB represent the volumes of components A and B in a solution, then the volume percentage of A is:
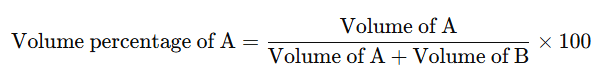
This is typically denoted as v/v. Sometimes, concentrations are also expressed as weight/volume (w/v). For example, a 10% solution of sodium chloride (w/v) means 10g of sodium chloride is dissolved in 100 mL of solution.
Example: If 50 mL of ethanol is mixed with 450 mL of water, what is the volume percentage of ethanol in the solution?
Solution: 
3. Parts per Million (ppm)
When a solute is present in very small amounts (trace quantities), the concentration is expressed in parts per million (ppm). This refers to the number of parts of a component per million parts of the solution.
It is calculated as:
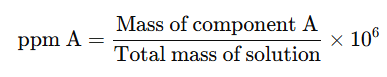
Example: suppose a litre of public supply water contains about 3×10−3g of chlorine. The mass percentage of chlorine is ?
Solution:
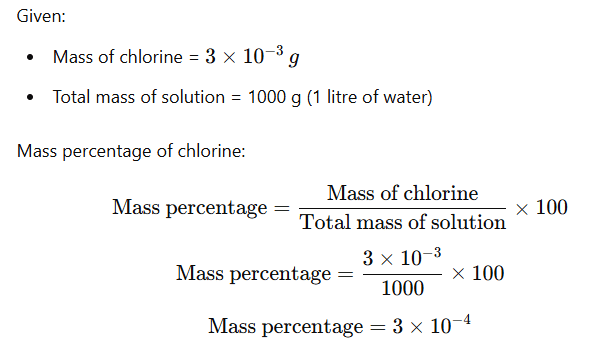
4. Molarity (M)
It is the number of moles of the solute dissolved per litre of the solution.
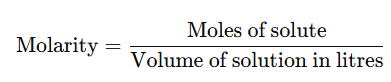
- It’s often convenient to express the volume in cm³ or mL, which leads to the formula:
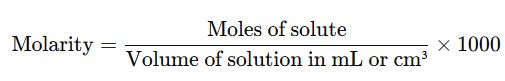
- (Since 1 litre = 1000 mL)
- The units of molarity are either moles per litre (mol L⁻¹) or moles per cubic decimetre (mol dm⁻³). The symbol M is used for mol L⁻¹ or mol dm⁻³ to represent molarity.
- Additionally, moles of solute can be calculated as:
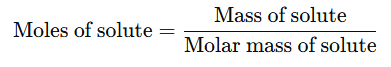
Example: 2.46 g of sodium hydroxide (with a molar mass of 40 g/mol) is dissolved in water, and the solution is made up to 100 cm³ in a volumetric flask. Calculate the molarity of the solution.
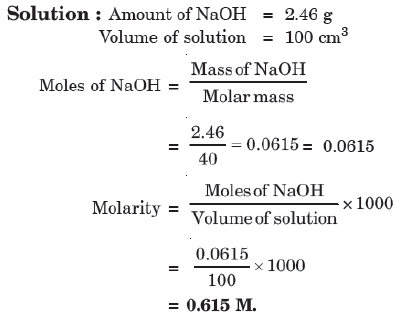
5. Molality (m)
No. of moles of solute present in 1000 gm of solvent.
 Alternatively, it can be expressed as:
Alternatively, it can be expressed as: 
- The units of molality are moles per kilogram (mol kg⁻¹), and it is represented by the symbol m.
Example: Calculate the molality of a solution containing 20.7 g of potassium carbonate dissolved in 500 mL of solution (assume density of solution = 1 g mL⁻¹).

6. Normality (N)
It is the number of gram equivalents of solute present in 1000 ml of solution.

Or

- The units of normality are gram equivalent per litre (g equiv L⁻¹).
- The gram equivalents of solute can be calculated using the formula:
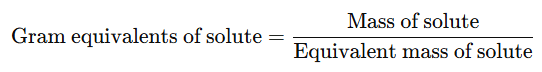
Example: Calculate the normality of solution containing 31.5 g of hydrated oxalic acid (H2C2O4⋅2H2O) in 1250 mL of solution.
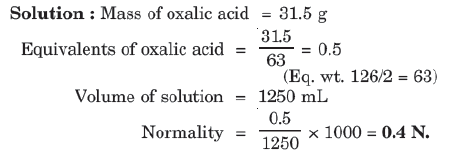
7. Mole Fraction
It is the ratio of number of moles of one component to the total number of moles present in the solution.
- The mole fraction of solute is denoted by 𝑥.
- Let’s assume a solution contains nA moles of solute and nB moles of solvent. The mole fraction of solute () is calculated as:

The mole fraction of solvent () is calculated as:

The sum of the mole fractions of all components in a solution is always equal to one, as shown below:

Thus, if the mole fraction of one component in a binary solution is known, the other can be determined. For example, the mole fraction is related to by the formula:
Example: A solution is prepared by adding 60 g of methyl alcohol to 120 g of water. Calculate the mole fraction of methanol and water.
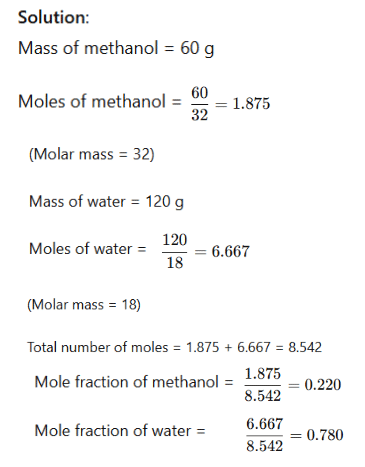
Relationship between Normality and Molarity of Solutions
- The normality and molarity of a solution are related by the formula:

- For Acids:

- where basicity is the number of H+H^+H+ ions that a molecule of acid can donate in solution.
- For Bases:

- where acidity is the number of OH− ions that a molecule of base can donate in solution.
8. Formality (f)
It is the number of formula mass in grams present per litre of solution.
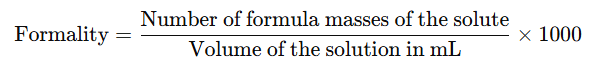
- This term is often used to describe the concentration of ionic substances (e.g., NaCl, KNO₃, CuSO₄), which do not exist as discrete molecules.
- In such cases, the term mole is not used to express concentration. Instead of molar mass, we use gram formula mass, which is the sum of the atomic masses of all atoms in the formula of the ionic compound.
Relationship between Molarity, Molality & Density of Solution
In solution chemistry, molarity (M), molality (m), and density (d) are important concentration measures. Here’s how they are related for a given solution:
- Molarity (M): This is the concentration of a solution in terms of moles of solute per liter of solution.
- Molality (m): This is the concentration of a solution in terms of moles of solute per kilogram of solvent.
- Density (d): The density of the solution, usually given in g/mL, relates mass to volume.
- Molar Mass (MM) : The molar mass of the solute (in g/mol), needed to link molarity and molality.
For a solution, if we have:
- "m" moles of solute dissolved in 1000 g of solvent,
- Then, the mass of this solution is 1000 + m x MM g.
The volume of this solution (in mL), using density, is given by: 
From this, we can derive the molarity (M) in terms of molality (m), density (d), and molar mass (MM):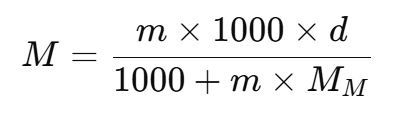
This formula helps convert between molarity and molality when the density of the solution and the molar mass of the solute are known.
Relationship between Molality & Mole Fraction
Consider a binary solution consisting of two components A (Solute) and B (Solvent).
Let xA & xB are the mole fraction of A & B respectively.
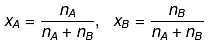
If molality of solution be m then
 =
= 
where MB is the molecular wt of the solvent B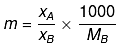

Examples
Example 1 : A bottle labeled with "12V H2O2" contains 700 ml solution. If a student mix 300 ml water in it what is the g/ liter strength & normality and volume strength of the final solution.
Solution. N = 12/5.6
Meq. of H2O2 = 12/5.6 x 100
let the normality of H2O2 on dilution be N.
Meq. before dilution = Meq. after dilution
N × 1000 = 12/5.6 x 100 N = 12/5.6 × 7/10 = 1.5 M = 1.5/2
strength gm/lit = 1.5/2 x 34 = 25.5
volume strength = N × 5.6 = 8.4 V
Example 2: Calculate the percentage of free SO3 in oleum (considered as a solution of SO3 in H2SO4) that is labeled '109% H2SO4 '.
Solution. '109% H2SO4' refers to the total mass of pure H2SO4, i.e., 109 g that will be formed when 100 g of oleum is diluted by 9 g of H2O which (H2O) combines with all the free SO3 present in oleum to form H2SO4.
H2O + SO3 → H2SO4
1 mole of H2O combines with 1 mole of SO3
or 18 g of H2O combines with 80 g of SO3
or 9 g of H2O combines with 40 g of SO3.
Thus, 100 g of oleum contains 40 g of SO3 or oleum contains 40% of free SO3.
Example 3: A 62% by mass of an aqueous solution of an acid has a specific gravity of 1.8. This solution is diluted such that the specific gravity of the solution became 1.2. Find the % by wt of acid in the new solution.
Solution. Density = 1.8
Volume of solution = Let x gm water be added in solution then
d = 0.6 x = 100
⇒ x = 166.67
Mass of new solution = 100 + 166.67 = 266.67
266.67 gm solution contains 62 gm of acid
% by mass = 23.24 %
Example 4: The density of 3 M solution of sodium thiosulphate (Na2S2O3) is 1.25 g/mL. Calculate
(i) amount of sodium thiosulphate
(ii) mole fraction of sodium thiosulphate
(iii) molality of Na and S2O32- ions
Solution.
(i) Let us consider one litre of sodium thiosulphate solution
wt. of the solution = density × volume (mL)
= 1.25 × 1000 = 1250 g.
wt. of Na2S2O3 present in 1 L of the solution
= molarity × mol. wt.
= 3 × 158 = 474 g.
wt. % of Na2S2O3 = 37.92%
(ii) Mass of 1 litre solution = 1.25 × 1000 g = 1250 g
[∵ density = 1.25 g/l]
Mole fraction of Na2S2O3 = Number of moles of Na2S2O3/Total number of moles
Moles of water = 1250 – 158 × 3/18 = 43.1
Mole fraction of Na2S2O3 = 3/3 + 43.1 = 0.065
(iii) 1 mole of sodium thiosulphate (Na2S2O3) yields 2 moles
of Na+ and 1 mole of S2O32-
Molality of Na2S2O3 = 3 × 1000/776 = 3.87
Molality of Na+ = 3.87 × 2 = 7.74 m
Molality of S2O2-3 = 3.87 m
Example 5: A solution of NaCl 0.5% by wt. If the density of the solution is 0.997 g/ml, calculate
(a) The molality
(b) Molarity
(c) Normality
(d) Mole fraction of the solute
Solution.
Number of moles of NaCl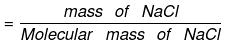 = 0.5/58.5 = 0.00854
= 0.5/58.5 = 0.00854
(a) By definition,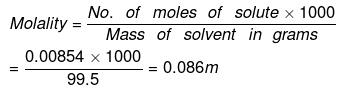
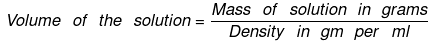 = 100/0.997 = 100.3
= 100/0.997 = 100.3
(b) Now Molarity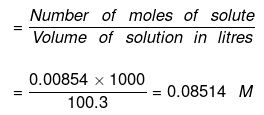
(c) Normality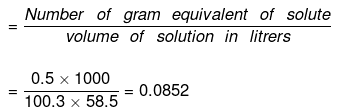
(d) To calculate the mole fraction of the solute
No. of moles of water in 99.5 g = 99.5/18 = 5.5277
Moles of NaCl = 0.5/58.5 = 8.547 x 10-3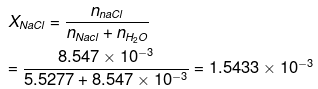 XH2O = 1 - XNaCI = 0.9984
XH2O = 1 - XNaCI = 0.9984
Tip: Practice makes a man perfect. Practice as many questions as you can on this topic. Make handwritten short notes for the formulas!
|
127 videos|245 docs|87 tests
|
FAQs on Stoichiometry & Concentration Terms - Chemistry Class 11 - NEET
| 1. What is stoichiometry and why is it important in chemistry? |  |
| 2. What are stoichiometric coefficients and how are they used in chemical equations? |  |
| 3. How do you calculate moles and what is the significance of the mole concept in chemistry? |  |
| 4. What is a limiting reagent and how does it affect chemical reactions? |  |
| 5. How do concentrations play a role in stoichiometric calculations in reactions in solutions? |  |

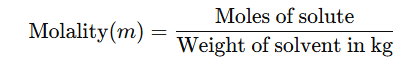 Alternatively, it can be expressed as:
Alternatively, it can be expressed as: