Syllabus: Electrical Engineering, GATE 2023 - Notes | Study GATE Past Year Papers for Practice (All Branches) - GATE

Introduction About GATE 2023

• Candidates are advised to refer to the EE syllabus while preparing for GATE. The GATE 2023 Electrical Engineering syllabus will help the candidates boost their preparation since they are made familiar with the topics asked in the exam. 
• The GATE 2023 examination will be conducted by the Indian Institute of Technology, KANPUR. Along with the GATE syllabus for electrical engineering, the candidates are also advised to check the exam pattern of GATE 2023 for preparation purposes.

Table: The overview of the GATE 2023 exam pattern for EEE.

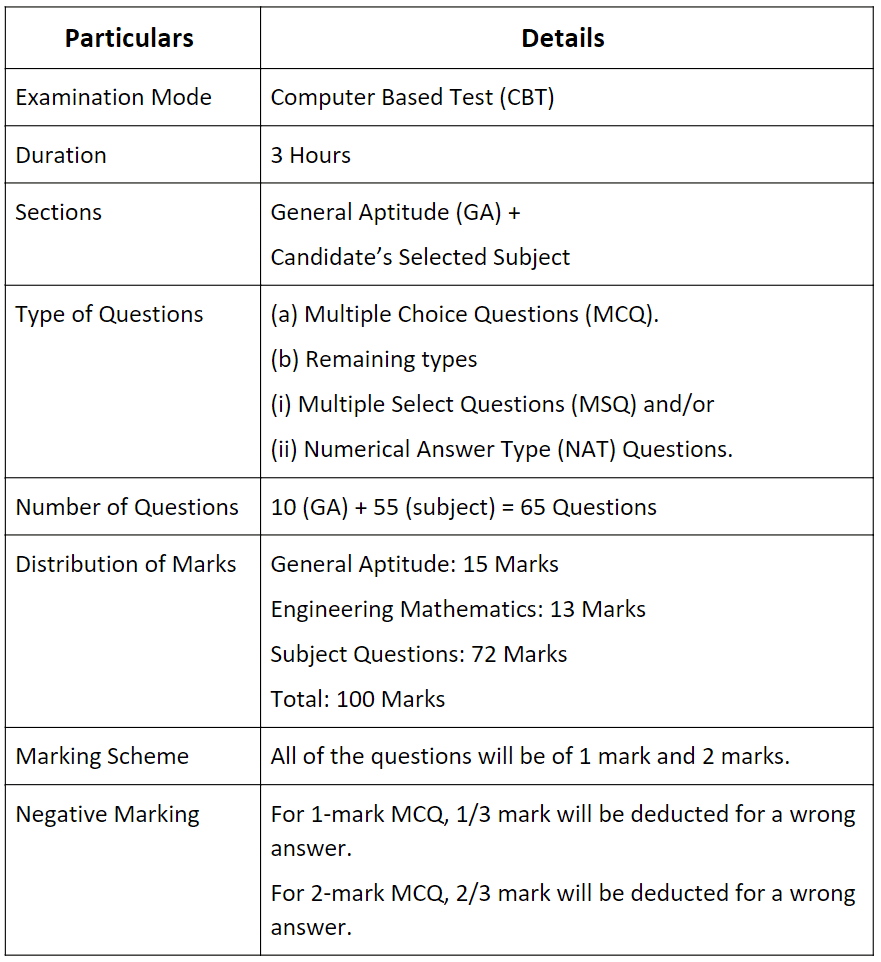
The three sections of the GATE EE paper are:
(i) General Aptitude
(ii) Engineering Mathematics
(iii) Subject-Specific Section

1. Engineering Mathematics 

• Linear Algebra: Matrix Algebra, Systems of linear equations, Eigenvalues, Eigenvectors.
  
• Calculus: Mean value theorems, Theorems of integral calculus, Evaluation of definite and improper integrals, Partial Derivatives, Maxima and minima, Multiple integrals, Fourier series, Vector identities, Directional derivatives, Line integral, Surface integral, Volume integral, Stokes’s theorem, Gauss’s theorem, Divergence theorem, Green’s theorem.
• Differential Equations: First order equations (linear and nonlinear), Higher order linear differential equations with constant coefficients, Method of variation of parameters, Cauchy’s equation, Euler’s equation, Initial and boundary value problems, Partial Differential Equations, Method of separation of variables.
• Complex Variables: Analytic functions, Cauchy’s integral theorem, Cauchy’s integral formula, Taylor series, Laurent series, Residue theorem, Solution integrals.
• Probability and Statistics: Sampling theorems, Conditional probability, Mean, Median, Mode, Standard Deviation, Random variables, Discrete and Continuous distributions, Poisson distribution, Normal distribution, Binomial distribution, Correlation analysis, Regression analysis.
• You can prepare Engineering Mathematics for GATE through EduRev’s Engineering Mathematics Course covering all the topics along with tests. 

2. Electric Circuits 

• Network elements: ideal voltage and current sources, dependent sources, R, L, C, M elements.
• Network solution methods: KCL, KVL, Node, and Mesh analysis;
• Network Theorems: Thevenin’s, Norton’s, Superposition and Maximum Power Transfer theorem, 
• Transient response of dc and ac networks
• Sinusoldal Steady State Analysis 
• Resonance
• Two-Port Networks
• Balanced three- phase Circuits: Star-delta transformation, Complex power
• A.C. Analysis: Power factor in ac circuits

3. Electromagnetic Fields 

• Electrostatic: Coulomb's Law, Electric Field Intensity, Electric Flux Density, Gauss's Law, Divergence, Electric field and potential due to point, line, plane, and spherical charge distributions, Effect of the dielectric medium, Capacitance of simple configurations.
• Magnetostatics: Biot‐Savart’s law, Ampere’s law, Curl, Faraday’s law, Lorentz force, Inductance, Magnetomotive force, Reluctance.
• Time Varying Electromagnetic Fields: Magnetic circuits, Self and Mutual inductance of simple configurations.

4. Signals and Systems 

• Introduction to Signal & Systems: Representation of continuous and discrete‐time signals, Shifting and scaling properties. Linear Time-Invariant and Causal systems
• Fourier Series representation of continuous and discrete-time periodic signals
• Sampling Theorem
• Applications of Fourier Transform for continuous and discrete-time signals, 
• Laplace Transform
• z-Transform

5. Electrical Machines 

• Single-phase transformers: equivalent circuit, phasor diagram, open circuit, and short circuit tests, regulation, and efficiency. 
• Three-phase transformers: connections, vector groups, parallel operation; Auto-transformer, Electromechanical energy conversion principles. 
• DC Machines: separately excited, series and shunt, motoring and generating mode of operation and their characteristics, speed control of dc motors. 
• Three-phase induction machines: the principle of operation, types, performance, torque-speed characteristics, no-load and blocked-rotor tests, equivalent circuit, starting, and speed control. Operating principle of single-phase induction motors.
• Synchronous machines: cylindrical and salient pole machines, performance and characteristics, regulation and parallel operation of generators, starting of synchronous motors. 
• Types of losses and efficiency calculations of electric machines.

6. Power Systems 

• Basic concepts of electrical power generation, ac and dc transmission concepts, Models and performance of transmission lines and cables, Series and shunt compensation, Electric field distribution and insulators.
• Distribution Systems
• Load Flow Studies: Per‐unit quantities, Bus admittance matrix, Gauss-Seidel, and Newton-Raphson load flow methods.
• Voltage and Frequency Control, Power factor correction.
• Symmetrical Components
• Symmetrical Fault Analysis 
• Unsymmetrical fault analysis
• Principles of overcurrent, differential, directional, and distance protection. 
• Circuit breakers, System stability concepts, Equal area criterion, Economic Load Dispatch (with and without considering transmission losses).

7. Control Systems 

• Basic of Control system & Transfer function: Mathematical modeling and representation of systems, Feedback principle, transfer function.
• Block diagram & Signal flow graphs
• Time Response Analysis: Transient and Steady‐state analysis of linear time-invariant systems
• Frequency Domain Analysis: Stability analysis using Routh-Hurwitz, and Nyquist criteria, Bode plots, root loci.
• Controller & Compensators: P, PI, and PID controllers, Lag, Lead and Lead‐Lag compensators.
• State Space Analysis: State-space model, Solution of state equations of LTI systems, R.M.S. value, average value calculation for any general periodic waveform.

8. Electrical and Electronic Measurements 

• Measurement & Measuring System: Measurement of voltage, current, power, energy and power factor, error analysis.
• Cathode Ray Oscilloscopes
• Bridge Measurement (AC & DC): Bridges and Potentiometers
• Instrument transformers
• Digital Voltmeters (DVM) and multimeters, Phase, Time and Frequency measurement. 

9. Analog and Digital Electronics 

• Simple diode circuits: clipping, clamping, rectifiers; Amplifiers: biasing, equivalent circuit and frequency response. oscillators and feedback amplifiers; operational amplifiers: characteristics and applications. 
• Single-stage active filters, Sallen Key, Butterworth, VCOs and timers, combinatorial and sequential logic circuits, multiplexers, demultiplexers, Schmitt triggers, sample and hold circuits, A/D and D/A converters.

10. Power Electronics 

• Thyristor: Static V-I characteristics and firing/gating circuits for Thyristor, MOSFET, IGBT 
• Choppers: Buck, Boost, and Buck-Boost Converters. 
• Rectifiers: Single and three-phase configuration of uncontrolled rectifiers. 
• Voltage and Current commutated Thyristor-based converters
• Bidirectional ac to dc voltage source converters. 
• Magnitude and Phase of line current harmonics for uncontrolled and thyristor-based converters. 
• Power factor and Distortion Factor of ac to dc converters. 
• Inverters: Single-phase and three-phase voltage and current source inverters, sinusoidal pulse width modulation.

1. Verbal Aptitude 

• Basic English grammar: tenses, articles, adjectives, prepositions, conjunctions, verb-noun agreement, and other parts of speech.
• Basic vocabulary: words, idioms, and phrases in context. 
• Reading Comprehension
• Narrative Sequencing

2. Quantitative Aptitude

• Data interpretation: data graphs (bar graphs, pie charts, and other graphs representing data), 2- and 3-dimensional plots, maps, and tables.
• Numerical computation and estimation: ratios, percentages, powers, exponents and logarithms, permutations and combinations, and series.
• Mensuration and Geometry
• Elementary Statistics and Probability

3. Analytical Aptitude 

• Logic: Deduction and Induction.
• Analogy
• Numerical Relations and Reasoning

4. Spatial Aptitude 

(a) Transformation of shapes: 

• Translation
• Rotation 
• Scaling 
• Mirroring
• Assembling 
• Grouping

(b) Paper folding
(c) Cutting

(d) Patterns in 2 and 3 dimensions.