Syllogism
What is Syllogism?
The word syllogism is derived from the Greek word "syllogismos" which means "conclusion, inference". Syllogisms are a logical argument of statements using deductive reasoning to arrive at a conclusion. The major contribution to the filed of syllogisms is attributed to Aristotle.
Statements of syllogisms
The questions of syllogisms of three main parts.
- Major premise
- Minor premise
- Conclusion
The central premise is a statement in general, believed to be true by the author.TRUE/FALSETry yourself: Observe the following statements and select if the conclusion is
Correct/ Incorrect
Example 1:
Major premise: All Actors are right-handed.
Minor premise: All right-handed are Artists.
The conclusion is: Some Artists are Actors.
Example: All women are smart.
The minor premise is a specific example of the major premise.
Example: Amanda is a woman.
The conclusion is a specific statement which logically follows both major and minor statement.
Example: Amanda is smart.
Steps to solve syllogism questions:
1. Note the number of variables present in the given statements
Ex: Man, doctor, pilot, etc.
2. Draw a Venn diagram corresponding to each variable; several Venn diagrams is equal to the number of variables.
3. Deduce the logical level by reading the statements and draw the corresponding Venn diagram
4. Check the conclusions given by comparing it with the Venn diagram obtained
5. Select the correct conclusion.
Identify the type A, E, I, O:
A ➜ Affirmative Positive
E ➜ Affirmative Negative
I ➜ Particular Positive
O ➜ Particular Negative
Understanding Syllogism with the help of Venn Diagram:
Different Types of Arguments
1. Affirmative Positive - A type
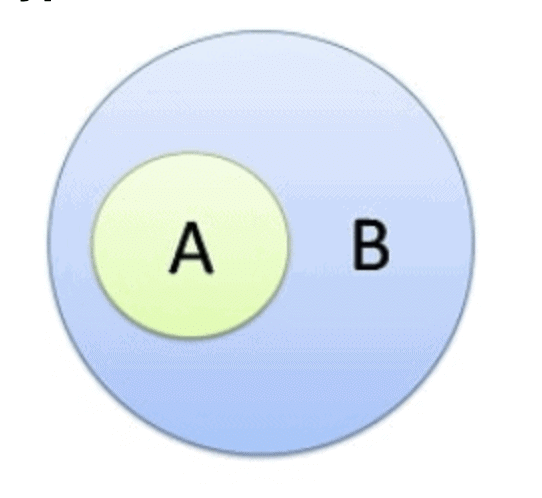
Example: All 'A' are 'B'.
From this statement, it can be inferred that:
- Some 'A' are 'B'.
- Some 'B' are 'A' is a definite conclusion.
Note: All 'B' are 'A' is a possibility but it may not be true in all cases
2. Affirmative Negative - E Type
Example: No 'A' are 'B'.
Conclusions which can be drawn from the given statement are:
- Some 'A' are Not 'B'.
- No 'B' are 'A'.
- Some 'B' are not 'A'.
3. Particular Positive - I Type
Example: Some 'A' are 'B'
From the given statement, we can conclude:
- Some 'B' are 'A'. (i)
- However, All 'A' are 'B'. (i)
- All 'B' are 'A'. (ii)
- Some 'A' are 'B'. (iii)
- Some 'A' are not 'B' and Some 'B' are not 'A' is not a definite conclusion.
4. Particular Negative - O Type
Example: Some 'A' are not 'B'.
It cannot be explained with a diagram. Moreover, no logical conclusion can be drawn from the given statement. There can be more than one possibilities in which this argument can be represented.
They are as under:
The shaded portion shows the A, which is not B.
Deriving Logical Conclusions When Various Types ofrguments are Given Together
1. All 'A' are 'B', All 'B' are 'C' (A & A)
This argument is represented below:
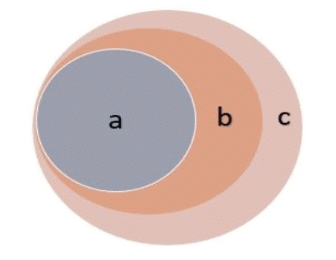Conclusions:
- All 'A' are 'C',
- Some 'C' are 'A',
- Some 'C' are 'B',
- Some 'A' are 'C'
- (All 'C' can be 'A', All 'B' can be 'A' but may not be defiantly true in all the cases.)
Try yourself: Statements: All the harmoniums are instruments. All the instruments are flutes.
Conclusions:
1. All the flutes are instruments.
2. All the harmoniums are flutes.
2. All 'A' are 'B', No 'B' are 'C' (A & E)
This argument is represented below:
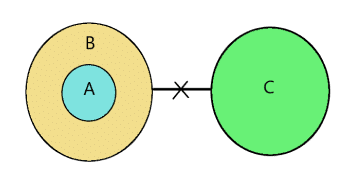
- No 'A' is 'C'.
- Some 'A' are not 'C'.
- Some 'C' are not 'A'.
- All 'A' are 'B'.
3. Some 'A' are 'B', All 'B' are 'C' (I & A)
This argument can be represented by Figure 9 as well as figure 10.
Conclusions which are definitely true in both the cases:
- Some 'A' are 'C'.
- Some 'C' are 'A'.
- Some 'B' are 'A'.
Try yourself: Statements: Some ships are boats. All boats are submarines. Some submarines are yatches. I. Some yatches are boats. II. Some submarines are boats. III. Some submarines are ships. IV. Some yatches are ships
Conclusion:
Note: All 'A' are 'C' , Some 'A' are not 'C' , Some 'A' are not 'B' and vice versa can be a possibility but may not be true in all the cases. The other possibility is as under.
4. Some 'A' are 'B', No 'B' are 'C' (I & E)
This argument can be represented by Figure 11, 12 & 13.
Conclusions which are definitely true in all the possible cases:
- Some 'A' are not 'C'.
- Some 'B' are not 'C'.
- No 'C' is 'B'.
- Some 'C' are not 'B'.
The shaded portion shows A which are not C.
Note: Any conclusion with 'C' as subject and 'A' as predicate is not a definite conclusion.
5. No 'A' are 'B', All 'B' are 'C' (E & A)
This argument can be represented by Figure 14, 15, & 16.
Conclusions which are definitely true in all the cases:
- Some 'C' are not 'A'.
- No 'B' is 'A'.
- Some 'B' are not 'A'.
- Some 'A' are not 'B'.
The shaded portion shows C, which are not A.
Note: Any conclusion with 'A' as subject and 'C' as predicate is not a definite conclusion.
6. No 'A' are 'B', Some 'B' are 'C' (E & I)
This argument can be represented by Figure 17, 18 & 19.
Conclusions which are definitely possible in all the cases:
- Some 'C' are not 'A'.
- Some 'A' are not 'B'.
- Some 'B' not 'A.'
Try yourself: Statements: Most CPUs are keyboards. No keyboard is a Mouse. All Mouses are CPU. I. Some keyboards are CPU II. All CPU’s are Mouse III. No Mouse is a keyboard IV. Some Mouse are keyboard
Conclusion:
Note: Any conclusion with 'A' as subject and 'C' as predicate is not a definite conclusion.
Try yourself: Statements: I. All fans are cylinders. II. Some cylinders are basins. Conclusions: I. Some basins are cylinders. II. No fan is a basin.
FAQs on Syllogism
| 1. What's the difference between standard form and non-standard form syllogisms in CLAT logical reasoning? |  |
| 2. How do I figure out if a syllogism conclusion is valid or invalid using the rules? | |
| 3. What does 'distribution of terms' really mean and why does it matter for syllogisms? | |
| 4. Why do I keep getting syllogism questions wrong when the answer seems obvious? | |
| 5. Can a syllogism have two negative premises and still be valid in CLAT exams? | |
