The Clausius-Clapeyron Equation | Chemistry Optional Notes for UPSC PDF Download
Evaporation
- In Section 23.3, the Clapeyron Equation was derived for melting points.

- However, our argument is actually quite general and should hold for vapor equilibria as well. The only problem is that the molar volume of gases are by no means so nicely constant as they are for condensed phases. (i. e., for condenses phases, both α and κ are pretty small).
- We can write:

as
- we can approximate

by just taking Further more if the vapor is considered an ideal gas, then
Further more if the vapor is considered an ideal gas, then
we get (23.4.1)
(23.4.1) - Equation 23.4.1 is known as the Clausius-Clapeyron equation. We can further work our the integration and find the how the equilibrium vapor pressure changes with temperature:

- Thus if we know the molar enthalpy of vaporization we can predict the vapor lines in the diagram. Of course the approximations made are likely to lead to deviations if the vapor is not ideal or very dense (e.g., approaching the critical point).
The Clapeyron Equation
- The Clapeyron attempts to answer the question of what the shape of a two-phase coexistence line is. In the P−T plane, we see the a function P(T), which gives us the dependence of P on T along a coexistence curve.
- Consider two phases, denoted α and β, in equilibrium with each other. These could be solid and liquid, liquid and gas, solid and gas, two solid phases, et. Let μα(P,T) and μβ(P,T) be the chemical potentials of the two phases. We have just seen that
μα(P,T) = μβ(P,T) (23.4.2) - Next, suppose that the pressure and temperature are changed by dP and dT. The changes in the chemical potentials of each phase are
dμα(P,T) = dμβ(P,T) (23.4.4)
(23.4.4) - However, since G(n,P,T) = nμ(P,T), the molar free energy G(P,T), which is G(n,P,T)/n, is also just equal to the chemical potential
 (23.4.5)
(23.4.5) - Moreover, the derivatives of G¯ are
 (23.4.6)
(23.4.6) - Applying these results to the chemical potential condition in Equation 23.4.4, we obtain
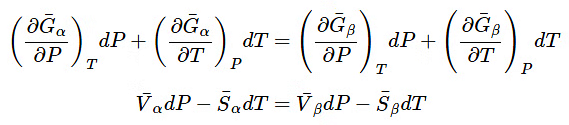 (23.4.7),(23.4.8)
(23.4.7),(23.4.8)
- Dividing through by dT, we obtain
 (23.4.9), (23.4.10),(23.4.11)
(23.4.9), (23.4.10),(23.4.11) - The importance of the quantity dP/dT is that is represents the slope of the coexistence curve on the phase diagram between the two phases. Now, in equilibrium dG=0, and since G=H−TS, it follows that dH = TdS at fixed T. In the narrow temperature range in which the two phases are in equilibrium, we can assume that H is independent of T, hence, we can write S=H/T. Consequently, we can write the molar entropy difference as
 (23.4.12)
(23.4.12)
and the pressure derivative dP/dT becomes (23.4.13)
(23.4.13)
a result known as the Clapeyron equation, which tells us that the slope of the coexistence curve is related to the ratio of the molar enthalpy between the phases to the change in the molar volume between the phases. If the phase equilibrium is between the solid and liquid phases, then and
and  respectively. If the phase equilibrium is between the liquid and gas phases, then
respectively. If the phase equilibrium is between the liquid and gas phases, then  respectively.
respectively. - For the liquid-gas equilibrium, some interesting approximations can be made in the use of the Clapeyron equation. For this equilibrium, Equation 23.4.13 becomes
 (23.4.14)
(23.4.14) - In this case,
 and we can approximate Equation 23.4.14 as
and we can approximate Equation 23.4.14 as (23.4.15)
(23.4.15) - Suppose that we can treat the vapor phase as an ideal gas. Certainly, this is not a good approximation so close to the vaporization point, but it leads to an example we can integrate. Since
 Equation 23.4.15 becomes
Equation 23.4.15 becomes (23.4.16), (23.4.17),(23.4.18)
(23.4.16), (23.4.17),(23.4.18) - which is called the Clausius-Clapeyron equation. We now integrate both sides, which yields

where C is a constant of integration. Exponentiating both sides, we find
P(T) = C′e−ΔH¯vap/RT
which actually has the wrong curvature for large T , but since the liquid-vapor coexistence line terminates in a critical point, as long as T is not too large, the approximation leading to the above expression is not that bad. - If we, instead, integrate both sides, the left from P1 to P2, and the right from T1 to T2, we find
 (23.4.19), (23.4.20),(23.4.21)
(23.4.19), (23.4.20),(23.4.21)
assuming that is independent of T. Here P1 is the pressure of the liquid phase, and P2 is the pressure of the vapor phase. Suppose we know P2 at a temperature T2, and we want to know P3 at another temperature T3. The above result can be written as
is independent of T. Here P1 is the pressure of the liquid phase, and P2 is the pressure of the vapor phase. Suppose we know P2 at a temperature T2, and we want to know P3 at another temperature T3. The above result can be written as (23.4.22)
(23.4.22)
Subtracting the two results, we obtain (23.4.23)
(23.4.23)
so that we can determine the vapor pressure at any temperature if it is known as one temperature.
In order to illustrate the use of this result, consider the following example:
Solved Examples
Example 1: At 1 bar, the boiling point of water is 373K. At what pressure does water boil at 473K ? Take the heat of vaporization of water to be 40.65kJ/mo4.
Ans: Let P1 = 1bar and T1=373K. Take T2=473K, and we need to calculate P2. Substituting in the numbers, we find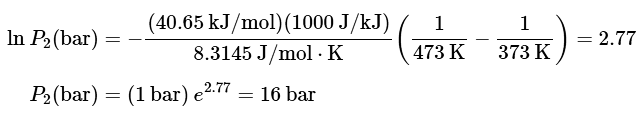
The vaporization curves of most liquids have similar shapes with the vapor pressure steadily increasing as the temperature increases (Figure 23.4.1).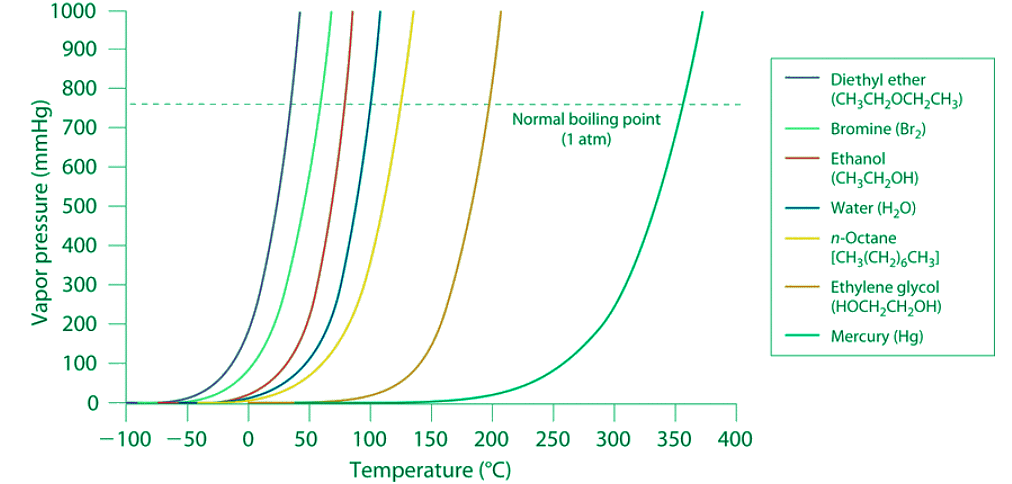 Figure 23.4.1: The Vapor Pressures of Several Liquids as a Function of Temperature. The point at which the vapor pressure curve crosses the P = 1 atm line (dashed) is the normal boiling point of the liquid.
Figure 23.4.1: The Vapor Pressures of Several Liquids as a Function of Temperature. The point at which the vapor pressure curve crosses the P = 1 atm line (dashed) is the normal boiling point of the liquid.
A good approach is to find a mathematical model for the pressure increase as a function of temperature. Experiments showed that the vapor pressure P and temperature T are related,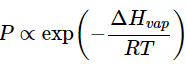 (23.4.26)
(23.4.26)
where ΔHvap is the Enthalpy (heat) of Vaporization and R is the gas constant (8.3145 J mol-1 K-1).
A simple relationship can be found by integrating Equation 23.4.26 between two pressure-temperature endpoints: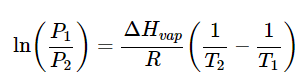 (23.4.27)
(23.4.27)
where P1 and P2 are the vapor pressures at two temperatures T1 and T2. Equation 23.4.27 is known as the Clausius-Clapeyron Equation and allows us to estimate the vapor pressure at another temperature, if the vapor pressure is known at some temperature, and if the enthalpy of vaporization is known.
Alternative Formulation
The order of the temperatures in Equation 23.4.27 matters as the Clausius-Clapeyron Equation is sometimes written with a negative sign (and switched order of temperatures):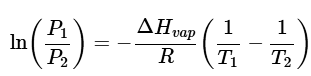 (23.4.28)
(23.4.28)
Example 2: The vapor pressure of water is 1.0 atm at 373 K, and the enthalpy of vaporization is 40.7 kJ mol-1. Estimate the vapor pressure at temperature 363 and 383 K respectively.
Ans: Using the Clausius-Clapeyron equation (Equation 23.4.28 23.4.28 ), we have: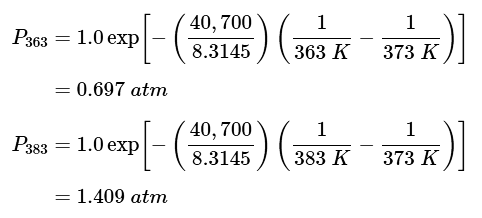
Note that the increase in vapor pressure from 363 K to 373 K is 0.303 atm, but the increase from 373 to 383 K is 0.409 atm. The increase in vapor pressure is not a linear process.
Advanced Note
- It is important to not use the Clausius-Clapeyron equation for the solid to liquid transition. That requires the use of the more general Clapeyron equation

- where
 is the molar change in enthalpy (the enthalpy of fusion in this case) and volume respectively between the two phases in the transition.
is the molar change in enthalpy (the enthalpy of fusion in this case) and volume respectively between the two phases in the transition.

|
Explore Courses for UPSC exam
|

|
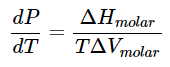
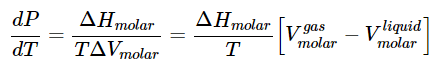
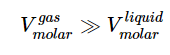
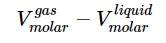
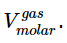 Further more if the vapor is considered an ideal gas, then
Further more if the vapor is considered an ideal gas, then
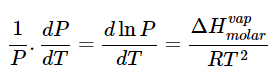 (23.4.1)
(23.4.1)
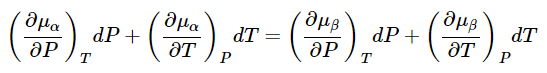 (23.4.4)
(23.4.4)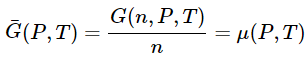 (23.4.5)
(23.4.5)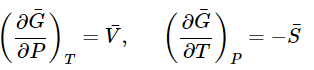 (23.4.6)
(23.4.6)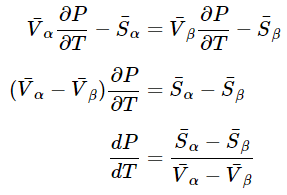 (23.4.9), (23.4.10),(23.4.11)
(23.4.9), (23.4.10),(23.4.11)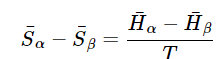 (23.4.12)
(23.4.12)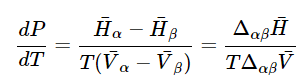 (23.4.13)
(23.4.13)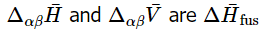 and
and 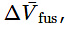 respectively. If the phase equilibrium is between the liquid and gas phases, then
respectively. If the phase equilibrium is between the liquid and gas phases, then 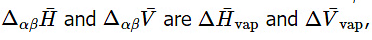 respectively.
respectively.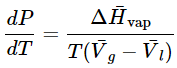 (23.4.14)
(23.4.14) and we can approximate Equation 23.4.14 as
and we can approximate Equation 23.4.14 as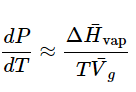 (23.4.15)
(23.4.15)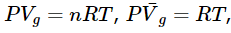 Equation 23.4.15 becomes
Equation 23.4.15 becomes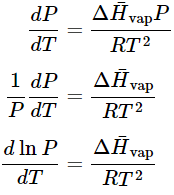 (23.4.16), (23.4.17),(23.4.18)
(23.4.16), (23.4.17),(23.4.18)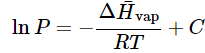
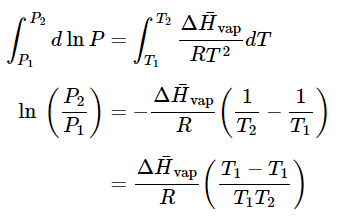 (23.4.19), (23.4.20),(23.4.21)
(23.4.19), (23.4.20),(23.4.21)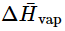 is independent of T. Here P1 is the pressure of the liquid phase, and P2 is the pressure of the vapor phase. Suppose we know P2 at a temperature T2, and we want to know P3 at another temperature T3. The above result can be written as
is independent of T. Here P1 is the pressure of the liquid phase, and P2 is the pressure of the vapor phase. Suppose we know P2 at a temperature T2, and we want to know P3 at another temperature T3. The above result can be written as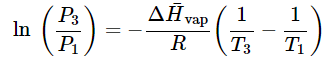 (23.4.22)
(23.4.22)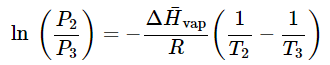 (23.4.23)
(23.4.23)
 is the molar change in enthalpy (the enthalpy of fusion in this case) and volume respectively between the two phases in the transition.
is the molar change in enthalpy (the enthalpy of fusion in this case) and volume respectively between the two phases in the transition.
















