Irodov Solutions: The Fundamental Equation of Dynamics | Physics Class 11 - NEET PDF Download
Q1: An aerostat of mass m starts coming down with a constant acceleration w. Determine the ballast mass to be dumped for the aerostat to reach the upward acceleration of the same magnitude. The air drag is to be neglected.
 View Answer
View Answer 
Ans. Let R be the constant upward thurst on the aerostat of mass m, coming down with a constant acceleration w. Applying Newton’s second law of motion for the aerostat in projection form
Fy = mwy
mg - R - mw (1)
Now, if Am be the mass, to be dumped, then using the Eq. Fy = mwy
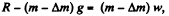 (2)
(2)
From Eqs. (1) and (2), w e get, 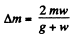
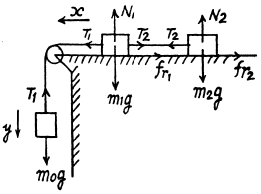
Q2: In the arrangement of Fig. 1.9 the masses m0, m1, and m2 of bodies are equal, the masses of the pulley and the threads are negligible, and there is no friction in the pulley. Find the acceleration w with which the body m0 comes down, and the tension of the thread binding together the bodies m1 and m2, if the coefficient of friction between these bodies and the horizontal surface is equal to k. Consider possible cases. 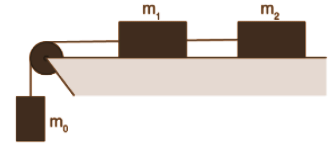
 View Answer
View Answer 
Ans. Let us write the fundamental equation of dynamics for all the three blocks in terms of projections, having taken the positive direction of x and y axes as shown in Fig; and using the fact that kinematical relation between the accelerations is such that the blocks move with same value of acceleration (say w)
 (1)
(1) (2)
(2)
and 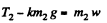 (3)
(3)
The simultaneous solution of Eqs. (1), (2) and (3) yields,
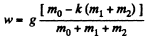
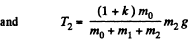
As the block m0 moves down with acceleration w, so in vector form
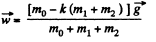
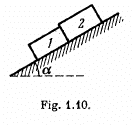
Q3: Two touching bars 1 and 2 are placed on an inclined plane forming an angle α with the horizontal (Fig. 1.10). The masses of the bars are equal to m1 and m2, and the coefficients of friction between the inclined plane and these bars are equal to k1 and k2 respectively, with k1 > k 2. Find:
(a) the force of interaction of the bars in the process of motion;
(b) the minimum value of the angle α at which the bars start sliding down.
 View Answer
View Answer 
Ans. Let us indicate the positive direction of Jt-axis along the incline (Fig.). Figures show the force diagram for the blocks.
Let, R be the force of interaction between the bars and they are obviously sliding down with the same constant acceleration w.
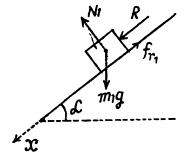
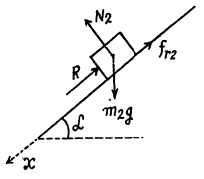
Newton’s second law of motion in projection form along x-axis for the blocks gives :
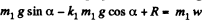 (1)
(1)
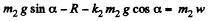 (2)
(2)
Solving Eqs. (1) and (2) simultaneously, we get
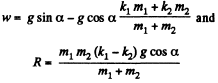
(b) when the blocks just slide down the plane, w = 0 , so from Eqn. (3)
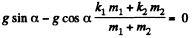
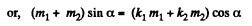
Hence 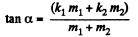
Q4: A small body was launched up an inclined plane set at an angle α = 15° against the horizontal. Find the coefficient of friction, if the time of the ascent of the body is η = 2.0 times less than the time of its descent.
 View Answer
View Answer 
Ans. Case 1. When the body is launched up:
Let k be the coefficient of friction, u the velocity of projection and l the distance traversed along the incline. Retarding force on the block = mg sin α + k mg cos α and hence the retardation = g sin α + k g cos α .
Using the equation of particle kinematics along the incline,
0 - u2-2 (g sin α + k g cos α) l
or, 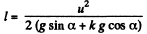 (1)
(1)
and 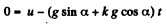
or, 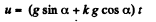 (2)
(2)
 (3)
(3)
Case (2). When the block comes downward, the net force on the body - mg sin a - km g cos a and hence its acceleration - g sin a - k g cos a Let, t be the time required then
 (4)
(4)
From Eqs. (3) and (4)
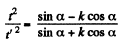
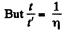 (according to the question),
(according to the question),
Hence on solving we get
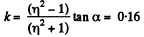
Q5: The following parameters of the arrangement of Fig. 1.11 are available: the angle α which the inclined plane forms with the horizontal, and the coefficient of friction k between the body m1 and the inclined plane. The masses of the pulley and the threads, as well as the friction in the pulley, are negligible. Assuming both bodies to be motionless at the initial moment, find the mass ratio m2/m1 at which the body m2
(a) starts coming down;
(b) starts going up;
(c) is at rest.
 View Answer
View Answer 
Ans. At the initial moment, obviously the tension in the thread connecting m1 and m2 equals the weight of m2.
(a) For the block m2 to come down or the block m1 to go up, the conditions is
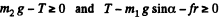
where T is tension and fr is friction which in the limiting case equals km1g cosα. Then
or 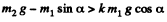
or 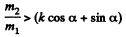
(b) Similarly in the case
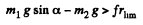
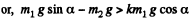
or, 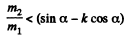

(c) For this case, neither kind o f motion is possible, and fr need not be limiting.
Hence, 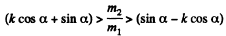
Q6: The inclined plane of Fig. 1.11 forms an angle α = 30° with the horizontal. The mass ratio m2/m1 = η = 2/3. The coefficient of friction between the body m1 and the inclined plane is equal to k = 0.10. The masses of the pulley and the threads are negligible. Find the magnitude and the direction of acceleration of the body m2 when the formerly stationary system of masses starts moving.
 View Answer
View Answer 
Ans. From the conditions, obtained in the previous problem, first we will check whether the mass m2 goes up or down.
Here, m2/ m1 = η > sin α + k cos α , (substituting the values). Hence the mass m2 will come down with an acceleration (say w). From the free body diagram of previous problem,
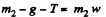 (1)
(1)
and 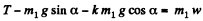 (2)
(2)
Adding (1) and (2), we get,
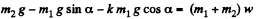
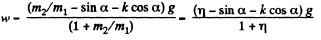
Substituting all the values, 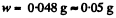
As m2 moves down with acceleration of magnitude w = .05 g > 0, thus in vector form acceleration of m2:
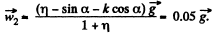
Q7: A plank of mass m1 with a bar of mass m2 placed on it lies on a smooth horizontal plane. A horizontal force growing with time t as F = at (a is constant) is applied to the bar. Find how the accelerations of the plank w1 and of the bar w2 depend on t, if the coefficient of friction between the plank and the bar is equal to k. Draw the approximate plots of these dependences.
 View Answer
View Answer 
Ans. Let us write the Newton’s second law in projection form along positive x-axis for the plank and the bar
fr - m1 w1, fr = m2 w2 (1)
At the initial moment, fr represents the static friction, and as the force F grows so does the friction force fr, but up to it’s limiting value
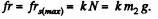
Unless this value is reached, both bodies moves as a single body with equal acceleration. But as soon as the force fr reaches the limit, the bar starts sliding over the plank i.e. 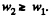
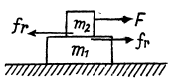
Substituting here the values of w1 and w2 taken from Eq. (1) and taking into account that
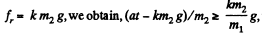
 corresponds to the moment
corresponds to the moment 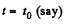
Hence, 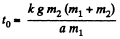
If 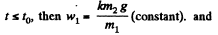
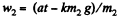
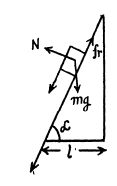
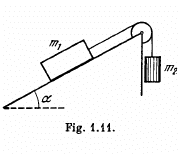
Q8: A small body A starts sliding down from the top of a wedge (Fig. 1.12) whose base is equal to l = 2.10 m. The coefficient of friction between the body and the wedge surface is k = 0.140. At what value of the angle a will the time of sliding be the least? What will it be equal to?
 View Answer
View Answer 
Ans. Apply Fx = m wx for body A
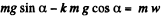
or, 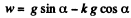
Now, from kinematical equation :
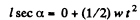
or, 
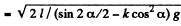
(using Eq. (1)).
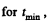
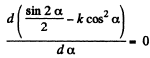
i.e. 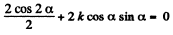
or, 
and putting the values of α , k and l in Eq . (2) we get 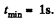
Q9: A bar of mass m is pulled by means of a thread up'an inclined plane forming an angle α with the horizontal (Fig. 1.13). The coefficient of friction is equal to k. Find the angle β which the thread must form with the inclined plane for the tension of the thread to be minimum. What is it equal to?
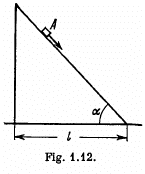
 View Answer
View Answer 
Ans. Let us fix the x - y co-ordinate system to the wedge, taking the x - axis up, along the incline and the y - axis perpendicular to it (Fig.).
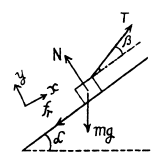
Let us apply Newton’s second law in projection form along x and y axis for the bar :
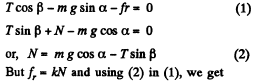
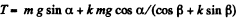 (3)
(3)
For Tmin the value of (cos β + k sin β ) should be maximum
So, 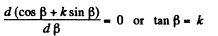
Putting this value of β in Eq. (3) we get,
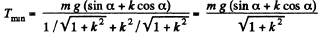
Q10: At the moment t = 0 the force F = at is applied to a small body of mass m resting on a smooth horizontal plane (a is a constant).
The permanent direction of this force forms an angle α with the horizontal (Fig. 1.14). Find:
(a) the velocity of the body at the moment of its breaking off the plane;
(b) the distance traversed by the body up to this moment.


 View Answer
View Answer 
Ans. First of all let us draw the free body diagram for the small body of mass m and indicate x - axis along the horizontal plane and y - axis, perpendicular to it, as shown in the figure.
Let the block breaks off the plane at 
So, 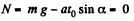
or, 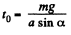 (1)
(1)
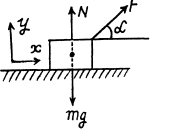
From  for the body under investigation :
for the body under investigation :
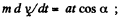 Integrating within the limits for v (t)
Integrating within the limits for v (t)
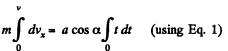
So, 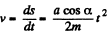 (2)
(2)
Integrating, Eqn. (2) for s (t)
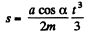 (3)
(3)
Using the value of t = t0 from Eq. (1), into Eqs. (2) and (3)
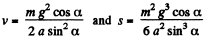
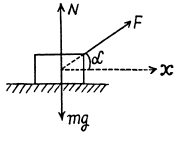
Q11: A bar of mass m resting on a smooth horizontal plane starts moving due to the force F = mg/3 of constant magnitude. In the process of its rectilinear motion the angle α between the direction of this force and the horizontal varies as α = as, where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle α.
 View Answer
View Answer 
Ans. Newton’s second law of motion in projection form, along horizontal or x - axis i.e.
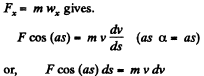
Integrating, over the limits for v (s)
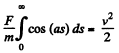
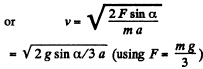
which is the sought relationship.
Q12: A horizontal plane with the coefficient of friction k supports two bodies: a bar and an electric motor with a battery on a block. A thread attached to the bar is wound on the shaft of the electric motor. The distance between the bar and the electric motor is equal to l. When the motor is switched on, the bar, whose mass is twice as great as that of the other body, starts moving with a constant acceleration w. How soon will the bodies collide?
 View Answer
View Answer 
Ans. From the Newton’s second law in projection from :
For the bar,
T - 2 kwg - (2 m) w (1)
For the motor,
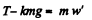 (2)
(2)
Now, from the equation of kinematics inthe frame of bar or motor
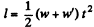 (3)
(3)
From (1), (2) and (3) wc get on eliminating T and W
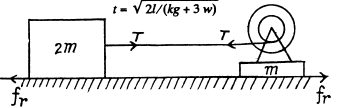
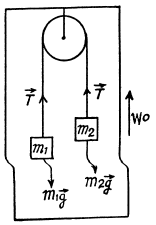
Q13: A pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the loads of masses m1 and m2. The car starts going up with an acceleration w0. Assuming the masses of the pulley and the thread, as well as the friction, to be negligible find:
(a) the acceleration of the load m1 relative to the elevator shaft and relative to the car;
(b) the force exerted by the pulley on the ceiling of the car.
 View Answer
View Answer 
Ans. Let us write Newton’s second law in vector from 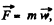 for both the blocks (in the frame ofjround).
for both the blocks (in the frame ofjround).

These two equations contain three unknown quantities 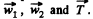 The third equation is provided by the kinematic relationship between the accelerations :
The third equation is provided by the kinematic relationship between the accelerations :
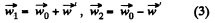
where 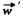 is th acceleration of the mass m1 with respect to the pulley or elevator car.
is th acceleration of the mass m1 with respect to the pulley or elevator car.
Summing up termwise the lelt hand and the right-hand sides of these kinematical equations, we get
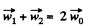 (4)
(4)
The simultaneous solution of Eqs* (1), (2) and (4) yield s
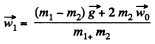
Using this result in Eq. (3) , we get,
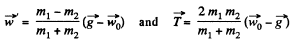
Using the results in Eq. (3) we get 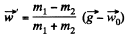
(b) obviously the force exerted by the pulley on the celing of the car
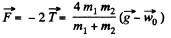
Note : one could also solve this problem in the frame of elevator car.
Q14: Find the acceleration w of body 2 in the arrangement shown in Fig. 1.15, if its mass is η times as great as the mass of bar l and the angle that the inclined plane forms with the horizontal is equal to α. The masses of the pulleys and the threads, as well as the friction, are assumed to be negligible. Look into possible cases.
 View Answer
View Answer 
Ans. Let us write Newton’s second law for both, bar 1 and body 2 in terms of projection having taken the positive direction of x1 and x2 as shown in the figure and assuming that body 2 starts sliding, say, upward along the incline
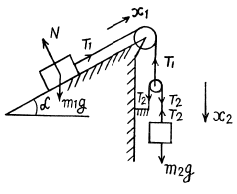
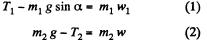
For the pulley, moving in vertical direction from the equation 
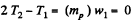
(as mass of the pulley mp = 0 )
or 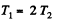 (3)
(3)
As the length of the threads are constant, the kinematical relation ship of accelerations becomes
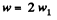 (4)
(4)
Simultaneous solutions of all these equations yields :
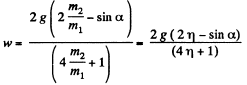
As η > 1, w is directed vertically downward, and hence in vector form
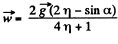
Q15: In the arrangement shown in Fig. 1.16 the bodies have masses m0, m1, m2 ,t he friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of the body m1. Look into possible cases.
 View Answer
View Answer 
Ans. Let us write Newton’s second law for masses m1 and m2 and moving pully in vertical direction along positive x - axis (Fig.) :
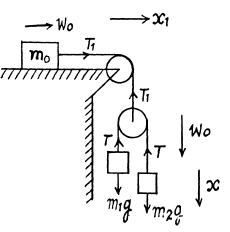
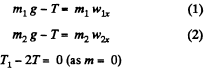
or 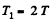 (3)
(3)
Again using Newton’s second law in projection form for mass m0 along positive x1 direction
(Fig.), we get
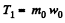 (4)
(4)
The kinematical relationship between the accelerations of masses gives in terms of projection on the x - axis
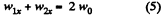
Simultaneous solution of the obtained five equations yields
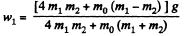
In vector form
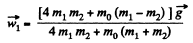
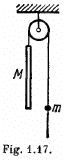
Q16: In the arrangement shown in Fig. 1.17 the mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion the ball got opposite the upper end of the rod. The rod length equals l.
 View Answer
View Answer 
Ans. As the thread is not tied with m, so if there were no friction between the thread and the ball m, the tension in the thread would be zero and as a result both bodies will have free fall motion. Obviously in the given problem it is the friction force exerted by the ball on the thread, which becomes the tension in the thread. From the condition or language of the problem wM > wm and as both are directed downward so , relative acceleration of M = wM > wm and is directed downward. Kinematical equation for the ball in the frame of rod in projection form along upward direction gives :
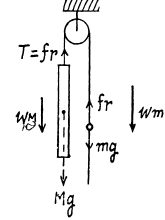
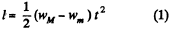
Newton’s second law in projection form along vertically down direction for both, rod and ball gives,
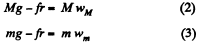
Multiplying Eq. (2) by m and Eq. (3) by M and then subtracting Eq. (3) from (2) and after using Eq. (1) we get
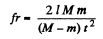
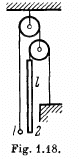
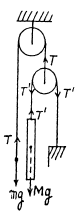
Q17: In the arrangement shown in Fig. 1.18 the mass of ball 1 is η = 1.8 times as great as that of rod 2. The length of the latter is l = 100 cm. The masses of the pulleys and the threads, as well as the friction, are negligible. The ball is set on the same level as the lower end of the rod and then released. How soon will the ball be opposite the upper end of the rod?
 View Answer
View Answer 
Ans. Suppose, the ball goes up with accleration w1 and the rod comes down with the acceleration w2. As the length of the thread is constant,
2 = w2 (1)
From Newton's second law in projection form along vertically upward for the ball and vertically downward for the rod respectively gives,
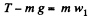 (2)
(2)
and 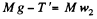 (3)
(3)
but T = 2T (because pulley is massless) (4)
From Eqs. (1), (2), (3) and (4)
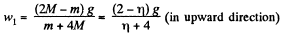
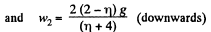
From kinematical equation in projection form, we get
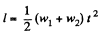
as, w1 and w2 are in the opposite direction.
Putting the values of w1 and w2, the sought time becomes
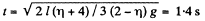
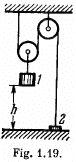
Q18: In the arrangement shown in Fig. 1.19 the mass of body 1 is η = 4.0 times as great as that of body 1. The height h = 20 cm. The masses of the pulleys and the threads, as well as the friction, are negligible. At a certain moment body 2 is released and the arrangement set in motion. What is the maximum height that body 2 will go up to?
 View Answer
View Answer 
Ans. Using Newton's second law in projection form along x - axis for the body 1 and along negative x - axis for the body 2 respectively, we get
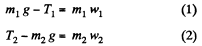
For the pulley lowering in downward direction from Newton's law along x axis,
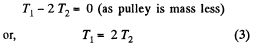
As the length of the thread is constant so,
w2 = 2w1 (4)

The simultaneous solution of above equations yields,
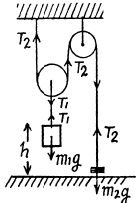
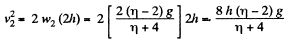 (5)
(5)
Obviously during the time interval in which the body 1 comes to the horizontal floor covering the distance h, the body 2 moves upward the distance 2h. At the moment when the body 2 is at the height 2h from the floor its velocity is given by the expression :
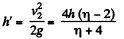
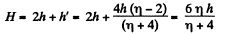
After the body m1 touches the floor the thread becomes slack or the tension in the thread zero, thus as a result body 2 is only under gravity for it's subsequent motion.
Owing to the velocity v2 at that moment or at the height 2h from the floor, the body 2 further goes up under gravity by the distance,
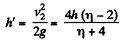
Thus the sought maximum height attained by the body 2 :
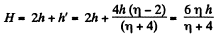
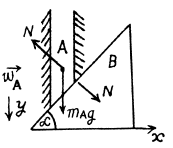
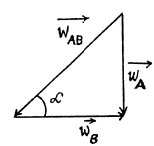
Q19: Find the accelerations of rod A and wedge B in the arrangement shown in Fig. 1.20 if the ratio of the mass of the wedge to that of the rod equals η, and the friction between all contact surfaces is negligible.
 View Answer
View Answer 
Ans. Let us draw free body diagram of each body, i.e. of rod A and of wedge B and also draw the kinemetical diagram for accelerations, after analysing the directions of motion of A and B. Kinematical relationship of accelarations is :
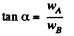 (1)
(1)
Let us write Newton’s second law for both bodies in terms of projections having taken positive directions of y and x axes as shown in the figure.
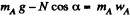 (2)
(2)
and 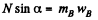 (3)
(3)
Simultaneous solution of (1), (2) and (3) yields :

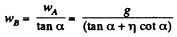
Note : We may also solve this problem using conservation of mechanical energy instead of Newton's second law.
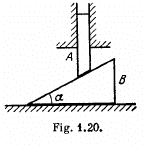
Q20: In the arrangement shown in Fig. 1.21 the masses of the wedge M and the body m are known. The appreciable friction exists only between the wedge and the body m, the friction coefficient being equal to k. The masses of the pulley and the thread are negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.
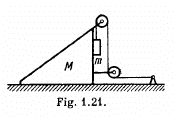
 View Answer
View Answer 
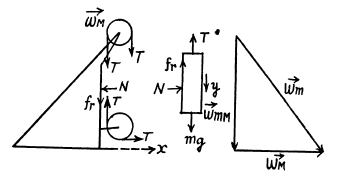
Ans. Let us draw free body diagram of each body and fix the coordinate system, as shown in the figure. After analysing the motion of M and m on the basis of force diagrams, let us draw the kinematical diagram for accelerations (Fig.).
As the length of threads are constant so,
 do not change their directions that why
do not change their directions that why
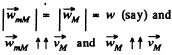
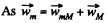
so, from the triangle law of vector addition
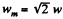 (1)
(1)
From the Eq. Fx = mwx , for the wedge and block :
T - N = Mw, (2)
and N = mw (3)
Now, from the Eq. Fy = mwy , for the block
mg - T - kN= mw (4)
Simultaneous solution of Eqs. (2), (3) and (4) yields :
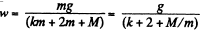
Hence using Eq. (1)
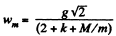
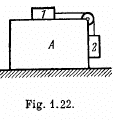
Q21: What is the minimum acceleration with which bar A (Fig. 1.22) should be shifted horizontally to keep bodies 1 and 2 stationary relative to the bar? The masses of the bodies are equal, and the coefficient of friction between the bar and the bodies is equal to k. The masses of the pulley and the threads are negligible, the friction in the pulley is absent.
 View Answer
View Answer 
Ans. Bodies 1 and 2 will remain at rest with repect to bar 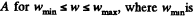 the sought minimum acceleration of the bar. Beyond these limits there will be a relative motion betw een b ar and the bodies.
the sought minimum acceleration of the bar. Beyond these limits there will be a relative motion betw een b ar and the bodies. 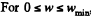 the tendency o f body 1 in relation to the bar A is to move towards right and is in the opposite sense for
the tendency o f body 1 in relation to the bar A is to move towards right and is in the opposite sense for 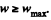 On the basis of above argument the static friction on 2 by A is directed upward and on 1 by A is directed towards le ft for the purpose o f calculating
On the basis of above argument the static friction on 2 by A is directed upward and on 1 by A is directed towards le ft for the purpose o f calculating 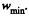 .
.
Let us write Newton’s second law for bodies 1 and 2 in terms of projection along positive x - axis (Fig.).
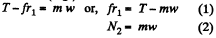
As body 2 has no acceleration in vertical direction, so
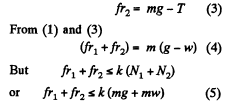

From (4) and (5)
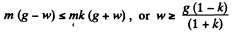
Hence
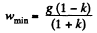
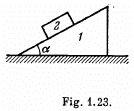
Q22: Prism 1 with bar 2 of mass m placed on it gets a horizontal acceleration w directed to the left (Fig. 1.23). At what maximum value of this acceleration will the bar be still stationary relative to the prism, if the coefficient of friction between them k< cot α?
 View Answer
View Answer 
Ans. On the basis of the initial aigument of the solution of Q.79, the tendency of bar 2 with respect to 1 will be to move up along the plane.
Let us fix (x - y) coordinate system in the frame o f ground as shown in the figure.
From second law of motion in projection form along y and x axes :
m g cos α - N = m w sin a

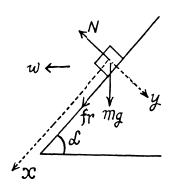
So, the sought maximum acceleration of the wedge :
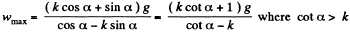
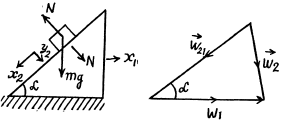
Q23: Prism 1 of mass m1 and with angle α (see Fig. 1.23) rests on a horizontal surface. Bar 2 of mass m2 is placed on the prism. Assuming the friction to be negligible, find the acceleration of the prism.
 View Answer
View Answer 
Ans. Let us draw the force diagram of each body, and on this basis we observe that the prism moves towards right say with an acceleration 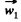 nd the bar 2 of mass moves down the plane with respect to 1, say with acceleration
nd the bar 2 of mass moves down the plane with respect to 1, say with acceleration 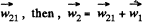 (Fig.)
(Fig.)
Let us write Newton’s second law for both bodies in projection form along positive y2 and x1 axes as shown in the Fig.
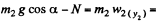
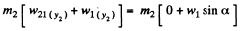
or, 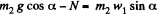 (1)
(1)
and 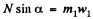 (2)
(2)
Solving (1) and (2), we get
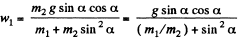
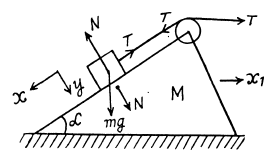
Q24: In the arrangement shown in Fig. 1.24 the masses m of the bar and M of the wedge, as well as the wedge angle α, are known. The masses of the pulley and the thread are negligible. The friction is absent. Find the acceleration of the wedge M.
 View Answer
View Answer 
Ans. To analyse the kinematic relations between the bodies, sketch the force diagram of each body as shown in the figure.
On the basis of force diagram, it is obvious that the wedge M will move towards right and the block will move down along the wedge. As the length of the thread is constant, the distance travelled by the block on the wedge must be equal to the distance travelled by the wedge on the flo&r. Hence 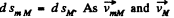 do not change their directions and acceleration that’s why
do not change their directions and acceleration that’s why 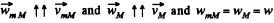 (say) and accordingly the diagram of kinematical dependence is shown in figure.
(say) and accordingly the diagram of kinematical dependence is shown in figure.
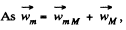 so from triangle law o f vector addition.
so from triangle law o f vector addition.
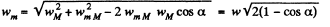 (1)
(1)
From Fx = m wx , (for the wedge),
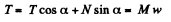 (2)
(2)
For the bar m let us fix (x - y) coordinate system in the frame of ground Newton ’s law in projection form along x and y axes (Fig.) gives
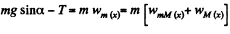
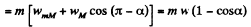 (3)
(3)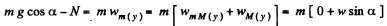 (4)
(4)
Solving the above Eqs. simultaneously, we get
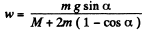
Note : We can study the motion of the block m in the frame of wedge also, alternately we may solve this problem using conservation of mechanical energy.
Q25: A particle of mass m moves along a circle of radius R. Find the modulus of the average vector of the force acting on the particle over the distance equal to a quarter of the circle, if the particle moves
(a) uniformly with velocity v;
(b) with constant tangential acceleration wτ the initial velocity being equal to zero.
 View Answer
View Answer 
Ans. Let us sketch the diagram for the motion of the particle of mass m along the circle of radius R and indicate x and y axis, as shown Jn the figure.
(a) For the particle, change in momentum 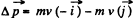
so , 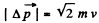
and time taken in describing quarter of the circle,
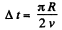
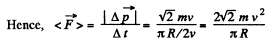

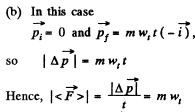
Q26: An aircraft loops the loop of radius R = 500 m with a constant velocity v = 360 km per hour. Find the weight of the flyer of mass m = 70 kg in the lower, upper, and middle points of the loop.
 View Answer
View Answer 
Ans. While moving in a loop, normal reaction exerted by the flyer on the loop at different points and uncom pensated weight if any contribute to the weight of flyer at those points,
(a) When the aircraft is at the lowermost point, Newton’s second law of motion in projection form Fn = mwn gives
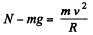
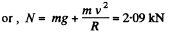
(b) When it is at the upper most point, again from Fn - mwn we get
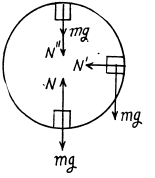
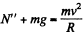
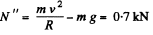
(c) When the aircraft is at the middle point of the loop, again from Fn = m wn
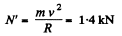
The uncompensated weight is mg. Thus effective weight 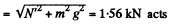 obliquely.
obliquely.
Q27: A small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released. Find:
(a) the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical;
(b) the thread tension at the moment when the vertical component of the sphere's velocity is maximum;
(c) the angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.
 View Answer
View Answer 
Ans. Let us depict the forces acting on the small sphere m, (at an arbitrary position when the thread makes an angle θ from the vertical) and write equation 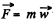 via projection on A
via projection on A
the unit vectors 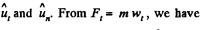
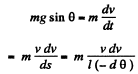
(as vertical is reference line of angular position)
or 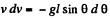
Integrating both the sides :
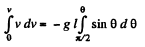
or, 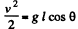

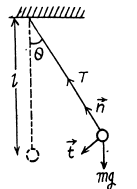
(Eq. (1) can be easily obtained by the conservation of mechanical energy).
From
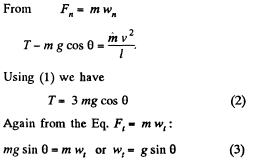
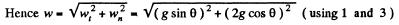
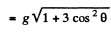
(b) Vertical component of velocity, vy = v sin θ
So, 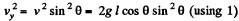
For maximum 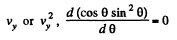
which yields 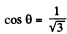
Therefore from 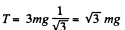
(c) We have 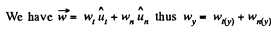
But in accordance with the problem wy = 0
So, 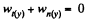
or, 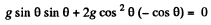
or, 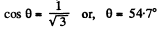
Q28: A ball suspended by a thread swings in a vertical plane so that its acceleration values in the extreme and the lowest position are equal. Find the thread deflection angle in the extreme position.
 View Answer
View Answer 
Ans. The ball has only normal acceleration at the lowest position and only tangential acceleration at any of the extreme position. Let v be the speed of the ball at its lowest position and l be the length of the thread, then according to the problem
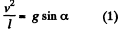
where α is the maximum deflection angle
From Newton’s law in projection form : Ft = mwt
or, 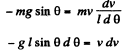
On integrating both the sides within their limits.

or,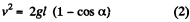
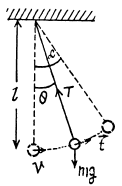
Note : Eq. (2) can easily be obtained by the conservation of mechanical energy of the ball in the uniform field of gravity.
From Eqs. (1) and (2) with θ = α
or, 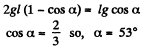
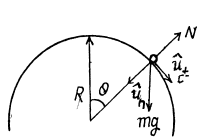
Q29: A small body A starts sliding off the top of a smooth sphere of radius R. Find the angle θ (Fig. 1.25) corresponding to the point at which the body breaks off the sphere, as well as the break-off velocity of the body.
 View Answer
View Answer 
Ans. Let us depict the forces acting on the body A(which are the force of gravity 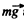 and the normal reaction
and the normal reaction 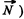 and write equation
and write equation 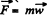 via projection on the unit vectors
via projection on the unit vectors 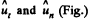
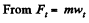
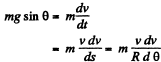
or, 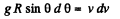
Integrating both side for obtaining v (θ)
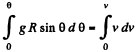
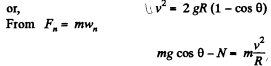
At the mom ent the body loses contact with the surface, N = 0 and therefore the Eq. (2) becomes
v2 = gR cos θ
where v and θ correspond to the moment when the body loses contact with the surface. Solving Eqs. (1) and (3) we obtain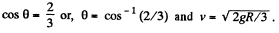
Q30: A device (Fig. 1.26) consists of a smooth L-shaped rod located in a horizontal plane and a sleeve A of mass m attached by a weight- less spring to a point B. The spring stiffness is equal to x. The whole system rotates with a constant angular velocity ω about a vertical axis passing through the point O. Find the elongation of the spring. How is the result affected by the rotation direction?
 View Answer
View Answer 
Ans. At first draw the free body diagram of the device as, shown. The forces, acting on the sleeve are it's weight, acting vertically downward, spring force, along the length of the spring and normal reaction by the rod, perpendicular to its length.
Let F be the spring force, and Δl be the elongation.
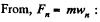
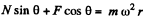 (1)
(1)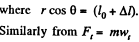
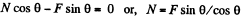 (2)
(2)
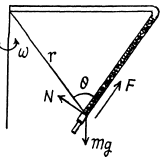
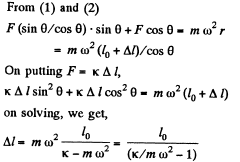
and it is independent of the direction of rotation.
Q31: A cyclist rides along the circumference of a circular horizontal plane of radius R, the friction coefficient being dependent only on distance r from the centre O of the plane as k = k0 (1—r/R), where k0 is a constant. Find the radius of the circle with the centre at the point along which the cyclist can ride with the maximum velocity. What is this velocity?
 View Answer
View Answer 
Ans. According to the question, the cyclist moves along the circular path and the centripetal force is provided by the frictional force. Thus from die equation Fn = m wn
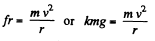
or, 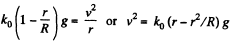 (1)
(1)
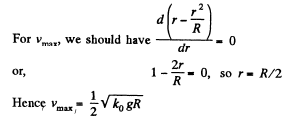
Q32: A car moves with a constant tangential acceleration wτ = 0.62 m/s2 along a horizontal surface circumscribing a circle of radius R = 40 m. The coefficient of sliding friction between the wheels of the car and the surface is k = 0.20. What distance will the car ride without sliding if at the initial moment of time its velocity is equal to zero?
 View Answer
View Answer 
Ans. As initial velocity is zero thus
v2 = 2 wts
As wt > 0 the speed of the car increases with time or distance. Till the moment, sliding starts, the static friction provides the required centripetal acceleration to the car.
Thus 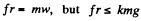
So, 
or, 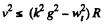
Hence 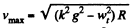
so, from Eqn. (1), the sought distance 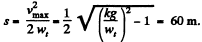
Q33: A car moves uniformly along a horizontal sine curve y = a sin (x/α), where a and α are certain constants. The coefficient of friction between the wheels and the road is equal to k. At what velocity will the car ride without sliding?
 View Answer
View Answer 
Ans. Since the car follows a curve, so the maximum velocity at which it can ride without sliding at the point of minimum radius of curvature is the sought velocity and obviously in this case the static friction between the car and the road is limiting.
Hence from the equation Fn = mw
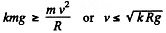
so 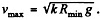 (1)
(1)
We know that, radius of curvature for a curve at any point (x, y) is given as,
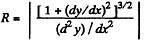 (2)
(2)
For the given curve,
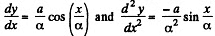
Substituting this value in (2) we get,
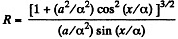
For the minimum 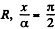
and therefore, corresponding radius of curvature
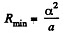 (3)
(3)
Hence from (1) and (2)
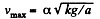
Q34: A chain of mass m forming a circle of radius R is slipped on a smooth round cone with half-angle θ. Find the tension of the chain if it rotates with a constant angular velocity co about a vertical axis coinciding with the symmetry axis of the cone.
 View Answer
View Answer 
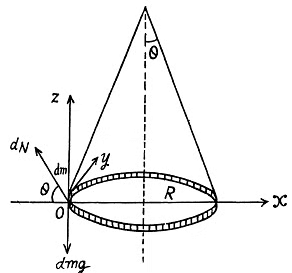
Ans. The sought tensile stress acts on each element of the chain. Hence divide the chain into small, similar elements so that each element may be assumed as a particle. We consider one such element of mass dm, which subtends angle d α at the centre. The chain moves along a circle of known radius R with a known angular speed ω and certain forces act on it We have to find one of these forces.
From Newton’s second law in projection form, Fx = mwx we get
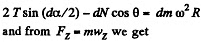
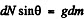
Then putting 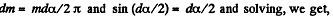
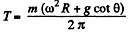
Q35: A fixed pulley carries a weightless thread with masses m1 and m2 at its ends. There is friction between the thread and the pulley. It is such that the thread starts slipping when the ratio m2/m1 = η0. Find:
(a) the friction coefficient;
(b) the acceleration of the masses when m2/m1 = η > η0.
 View Answer
View Answer 
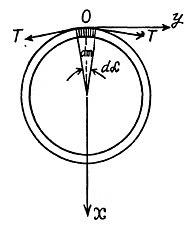
Ans. Let, us consider a small element of the thread and draw free body diagram for this element, (a) Applying Newton’s second law of motion in projection form, Fn = mwn for this element,
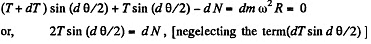
or, 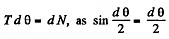 (1)
(1)
Also, 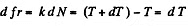 (2)
(2)
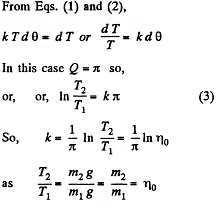
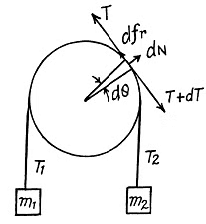
(b) When 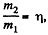 which is greater than η0 the blocks will move with same value of acceleration, (say w) and clearly m2 moves downward. From Newton’s second law in projection form (downward for m2 and upward for m1) we get :
which is greater than η0 the blocks will move with same value of acceleration, (say w) and clearly m2 moves downward. From Newton’s second law in projection form (downward for m2 and upward for m1) we get :
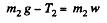 (4)and
(4)and 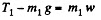 (5)
(5)
Also 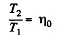 (6)
(6)
Simultaneous solution of Eqs. (4), (5) and (6) yields :
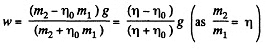
Q36: A particle of mass m moves along the internal smooth surface of a vertical cylinder of radius R. Find the force with which the particle acts on the cylinder wall if at the initial moment of time its velocity equals v0 and forms an angle α with the horizontal.
 View Answer
View Answer 
Ans. The force with which the cylinder wall acts on the particle will provide centripetal force necessary for the motion of the particle> and since there is no acceleration acting in the horizontal direction, horizontal component of the velocity will remain constant througout the motion.
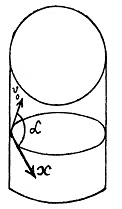
So vx = v0 cos α
Using, Fn = m wn, for the particle of mass m,
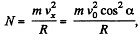
which is the required normal force.
Q37: Find the magnitude and direction of the force acting on the particle of mass m during its motion in the plane xy according to the law x = a sin ωt, y = b cos ωt, where a, b, and ω are constants.
 View Answer
View Answer 
Ans. Obviously the radius vector describing the position of the particle relative to the origin of coordinate is
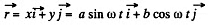
Differentiating twice with respect the time :
 (1)
(1)
Thus 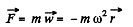
Q38: A body of mass m is thrown at an angle to the horizontal with the initial velocity v0. Assuming the air drag to be negligible, find:
(a) the momentum increment Δp that the body acquires over the first t seconds of motion;
(b) the modulus of the momentum increment Δp during the total time of motion.
 View Answer
View Answer 
Ans. 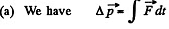
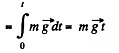 (1)
(1)
(b) Using the solution of problem 1.28 (b), the total time of motion 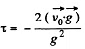
Hence using 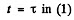
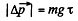
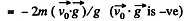
Q39: At the moment t = 0 a stationary particle of mass in experiences a time-dependent force F = at (τ — t), where a is a constant vector, τ is the time during which the given force acts. Find:
(a) the momentum of the particle when the action of the force discontinued;
(b) the distance covered by the particle while the force acted.
 View Answer
View Answer 
Ans. From the equation o f the g iven time dependence force 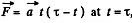 the force vanishes,
the force vanishes,
(a) Thus 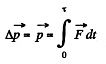
or, 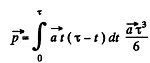 but
but 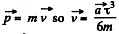
(b) Again from the equation 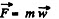 or,
or, 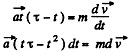 Integrating w ithin the limits for
Integrating w ithin the limits for 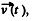
 or,
or, 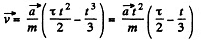
Thus 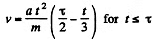
Hence distance covered during the tim e interval t = τ,
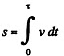
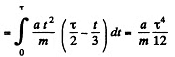
Q40: At the moment t = 0 a particle of mass m starts moving due to a force F = F0 sin ωt, where F0 and ω are constants. Find the distance covered by the particle as a function of t. Draw the approximate plot of this function.
 View Answer
View Answer 
Ans. We have 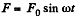
or 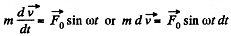
On integrating,
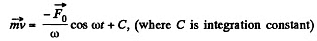
When

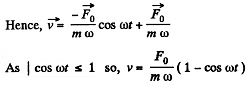
Thus 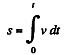
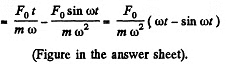
Q41: At the moment t = 0 a particle of mass m starts moving due to a force F = F0 cos ωt, where F0 and ω are constants. How long will it be moving until it stops for the first time? What distance will it traverse during that time? What is the maximum velocity of the particle over this distance?
 View Answer
View Answer 
Ans. According to the problem, the force acting on the particle of mass m 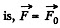 cos ωt
cos ωt
So, 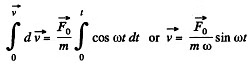
Integrating, within the limits.
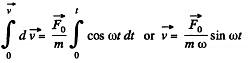
It is clear from equation (1), that after starting at t = 0, die particle comes to rest fro the first time at 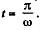
From Eqn. (1), 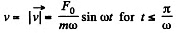 (2)
(2)
Thus during the time interval t = π/ω, the sought distance
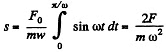
From Eq. (1)
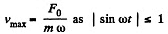
Q42: A motorboat of mass m moves along a lake with velocity v0. At the moment t = 0 the engine of the boat is shut down. Assuming the resistance of water to be proportional to the velocity of the boat F = —rv, find:
(a) how long the motorboat moved with the shutdown engine;
(b) the velocity of the motorboat as a function of the distance covered with the shutdown engine, as well as the total distance covered till the complete stop;
(c) the mean velocity of the motorboat over the time interval (beginning with the moment t = 0), during which its velocity decreases η times.
 View Answer
View Answer 
Ans. (a) From the problem 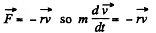
Thus 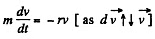
or, 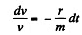
On integrating 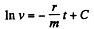
But at 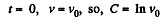
or, 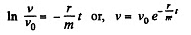
Thus for 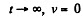
(b) We have 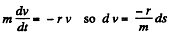
Integrating within the given limits to obtain v (s):
or, 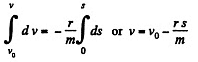
Thus for 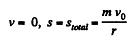
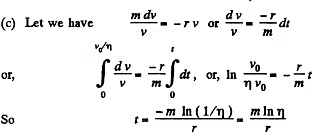
Now, average velocity over this time interval,
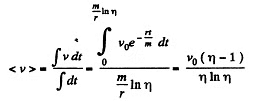
Q43: Having gone through a plank of thickness h, a bullet changed its velocity from v0 to v. Find the time of motion of the bullet in the plank, assuming the resistance force to be proportional to the square of the velocity.
 View Answer
View Answer 
Ans. According to the problem
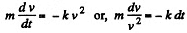
Integrating, withing the limits,
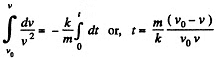
To find the valufc of k, rewrite
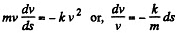
On integrating
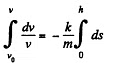
So, 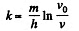 (2)
(2)
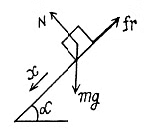
Putting the value of k from (2) in (1), we get
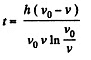
Q44: A small bar starts sliding down an inclined plane forming an angle α with the horizontal. The friction coefficient depends on the distance x covered as k = ax, where a is a constant. Find the distance covered by the bar till it stops, and its maximum velocity over this distance.
 View Answer
View Answer 
Ans. From Newton’s second law for the bar in projection from, Fx = m wx along x direction
we get 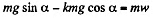
or, 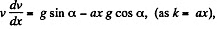
or, 
or, 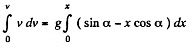
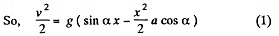
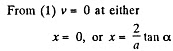
 As the motion of the bar is unidirectional it stops after going through a distance of
As the motion of the bar is unidirectional it stops after going through a distance of 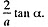
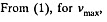
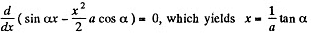 Hence, the maximum velocity will be at the distance, x = tan α/a Putting this value of x in (1) the maximum velocity,
Hence, the maximum velocity will be at the distance, x = tan α/a Putting this value of x in (1) the maximum velocity,
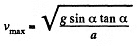
Q45: A body of mass m rests on a horizontal plane with the friction coefficient lc. At the moment t = 0 a horizontal force is applied to it, which varies with time as F = at, where a is a constant vector. Find the distance traversed by the body during the first t seconds after the force action began.
 View Answer
View Answer 
Ans. Since, the applied force is proportional to the time and the frictional force also exists, the motion does not start just after applying the force. The body starts its motion when F equals the limiting friction.
Let the motion start after time t0 , then
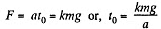
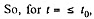 the body remains at rest and for t > t0 obviously
the body remains at rest and for t > t0 obviously
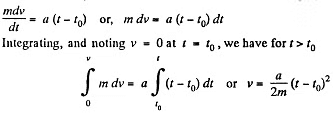
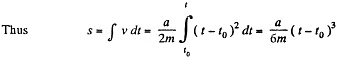
Q46: A body of mass m is thrown straight up with velocity vo. Find the velocity v' with which the body comes down if the air drag equals kv2, where k is a constant and v is the velocity of the body.
 View Answer
View Answer 
Ans. While going upward, from Newton’s second law in vertical direction :

At the maximum height h, the speed v = 0, so
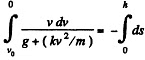
Integrating and solving, we get,
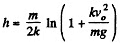 (1)
(1)
When the body falls downward, the net force acting on the body in downward direction equals 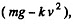
Hence net acceleration, in downward direction, according to second law of motion
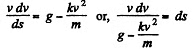
Thus, 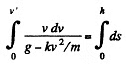
Integrating and putting the value of h from (1), we get,
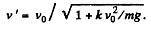
Q47: A particle of mass m moves in a certain plane P due to a force F whose magnitude is constant and whose vector rotates in that plane with a constant angular velocity ω. Assuming the particle to be stationary at the moment t = 0, find:
(a) its velocity as a function of time;
(b) the distance covered by the particle between two successive stops, and the mean velocity over this time.
 View Answer
View Answer 
Ans. Let us fix x - y co-ordinate system to the given plane, taking x-axis in the direction along which the force vector was oriented at the moment t = 0 , then the fundamental equation of dynamics expressed via the projection on x and y-axes gives,
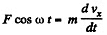 (1)and
(1)and 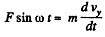 (2)
(2)
(a) Using the condition  (3)
(3)
and
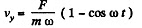 (4)
(4)
Hence, 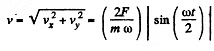
(b) It is seen from this that the velocity v turns into zero after the time interval Δt, which can be found from the relation ,
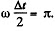 Consequently, the sought distance, is
Consequently, the sought distance, is
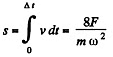
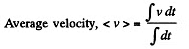
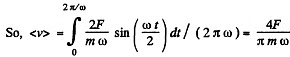
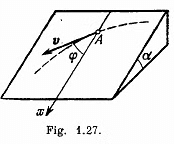
Q48: A small disc A is placed on an inclined plane forming an angle a with the horizontal (Fig. 1.27) and is imparted an initial velocity v0. Find how the velocity of the disc depends on the angle y if the friction coefficient k = tan α and at the initial moment yo = = π/2.
 View Answer
View Answer 
Ans. The acceleration of the disc along the plane is determined by the projection of the force of gravity on this plane Fx = mg sin α and the friction force fr = kmg cos α . In our case k = tan α and therefore
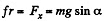
Let us find the projection of the acceleration on the derection of the tangent to the trajectory and on the x-axis :
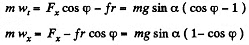
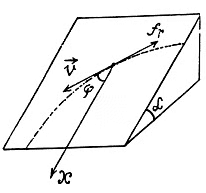
It is seen fromthis that wt = - wx, which means that the velocity v and its projection vx differ only by a constant value C which does not change with time, i.e.
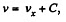
where 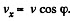 . The constant C is found from the initial condition v = v0, whence
. The constant C is found from the initial condition v = v0, whence 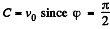 initially. Finally we obtain
initially. Finally we obtain
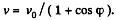
In the cource of time 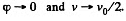 (Motion then is unaccelerated.)
(Motion then is unaccelerated.)
Q49: A chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain 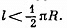
 View Answer
View Answer 
Ans. Let us consider an element of length ds at an angle qp from the vertical diameter. As the speed of this element is zero at initial instant of time, it's centripetal acceleration is zero, and hence,  where λ is the linear mass density o f the chain Let
where λ is the linear mass density o f the chain Let 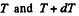 be the tension at the upper and the lower ends of ds. we have from,
be the tension at the upper and the lower ends of ds. we have from, 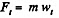
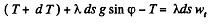 or,
or, 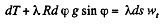
If we sum the above equation for all elements, the term 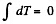 because there is no tension at the free ends, so
because there is no tension at the free ends, so
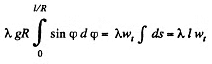

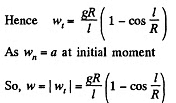
Q50: A small body is placed on the top of a smooth sphere of radius R. Then the sphere is imparted a constant acceleration w0 in the horizontal direction and the body begins sliding down. Find:
(a) the velocity of the body relative to the sphere at the moment of break-off;
(b) the angle θ0 between the vertical and the radius vector drawn from the centre of the sphere to the break-off point; calculate θ0 for w0 = g.
 View Answer
View Answer 
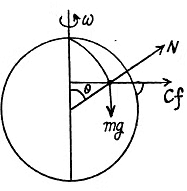
Ans. In the problem, we require the velocity of the body, relative to the sphere, which itself moves with an acceleration w0 in horizontal direction (say towards left). Hence it is advisible to solve the problem in the frame of sphere (non-inertial frame).
At an arbitary moment, when the body is at an angle θ with the vertical, we sketch the force diagram for the body and write the second law of motion in projection form
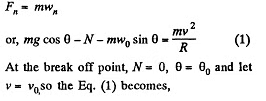
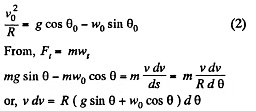
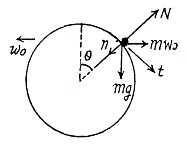
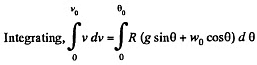
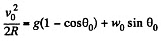 (3)
(3)
Note that the Eq. (3) can also be obtained by the work-energy theorem A = ΔT (in the frame of sphere)
therefore, 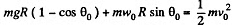
 or,
or, 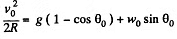 Solving Eqs. (2) and (3) we get,
Solving Eqs. (2) and (3) we get,
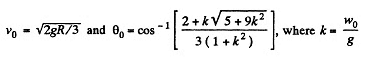
Hence 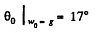
Q51: A particle moves in a plane under the action of a force which is always perpendicular to the particle's velocity and depends on a distance to a certain point on the plane as 1/rn, where n is a constant. At what value of n will the motion of the particle along the circle be steady?
 View Answer
View Answer 
Ans. This is not central force problem unless the path is a circle about the said point. Rather here Ft (tangential force) vanishes. Thus equation of motion becomes,
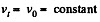
and, 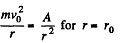
We can consider the latter equation as the equilibrium under two forces. When the motion is perturbed, we write r = r0 + x and the net force acting on the particle is,
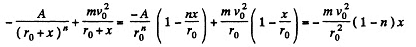
This is opposite to the displacement 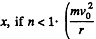 is an outward directed centrifugal force while
is an outward directed centrifugal force while 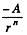 is the inward directed external force).
is the inward directed external force).
Q52: A sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R (Fig. 1.28). The system is set in rotation with a constant angular velocity ω about a vertical axis OO'. Find the angle θ corresponding to the steady position of the sleeve.
 View Answer
View Answer 
Ans. There are two forces on the sleeve, the weight F1 and the centrifugal force F2. We resolve both forces into tangential and normal component then the net downward tangential force on the sleeve is,
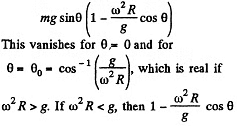
is always positive for small values of 0 and hence the net tangential force near θ = 0 opposes any displacement away from it. θ = 0 is then stable.
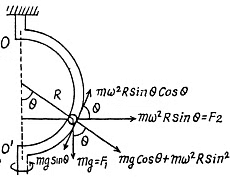

However 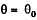 is stable because the force tends to bring the sleeve near the equilibrium position
is stable because the force tends to bring the sleeve near the equilibrium position 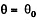
If ω2R = g, the two positions coincide and becomes a stable equilibrium point.
Q53: A rifle was aimed at the vertical line on the target located precisely in the northern direction, and then fired. Assuming the air drag to be negligible, find how much off the line, and in what direction, will the bullet hit the target. The shot was fired in the horizontal direction at the latitude φ = 60°, the bullet velocity v = 900 m/s, and the distance from the target equals s = 1.0 km.
 View Answer
View Answer 
Ans. Define the axes as shown with z along the local vertical, x due east and y due north. (We assume we are in the northern hemisphere). Then the Coriolis force has the components.
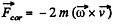
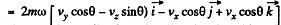
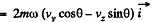
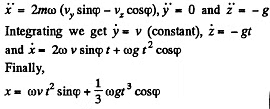
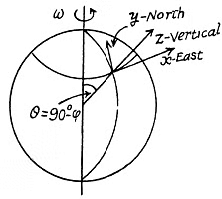
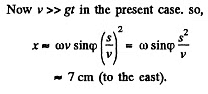
Q54: A horizontal disc rotates with a constant angular velocity ω = 6.0 rad/s about a vertical axis passing through its centre. A small body of mass m = 0.50 kg moves along a diameter of the disc with a velocity v' = 50 cm/s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r = 30 cm from the rotation axis.
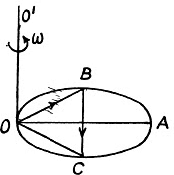
 View Answer
View Answer 
Ans. The disc exerts three forces which are mutually perpendicular. They are the reaction of the weight, mgy vertically upward, the Coriolis force 2mv' ω perpendicular to the plane of the vertical and along the diameter, and mω2r outward along the diameter. The resultant force is,
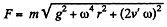
Q55: A horizontal smooth rod AB rotates with a constant angular velocity ω = 2.00 rad/s about a vertical axis passing through its end A. A freely sliding sleeve of mass m = 0.50 kg moves along the rod from the point A with the initial velocity v0 = 1.00 m/s. Find the Coriolis force acting on the sleeve (in the reference frame fixed to the rotating rod) at the moment when the sleeve is located at the distance r = 50 cm from the rotation axis.
 View Answer
View Answer 
Ans. The sleeve is free to slide along the rod AB. Thus only the centrifugal force acts on it.
The equation is,

so, 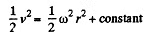 or,
or, 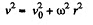
v0 being the initial velocity when r = 0. The Coriolis force is then,
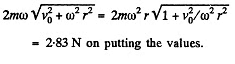
Q56: A horizontal disc of radius R rotates with a constant angular velocity ω about a stationary vertical axis passing through its edge. Along the circumference of the disc a particle of mass m moves with a velocity that is constant relative to the disc. At the moment when the particle is at the maximum distance from the rotation axis, the resultant of the inertial forces Fin acting on the particle in the reference frame fixed to the disc turns into zero. Find:
(a) the acceleration ω' of the particle relative to the disc;
(b) the dependence of Fin on the distance from the rotation axis.
 View Answer
View Answer 
Ans. The disc OBAC is rotating with angular velocity ω about the axis OO' passing through the edge point O. The equation of motion in rotating frame is,
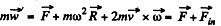
where 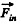 is the resultant inertial force. (pseudo force) which is the vector sum of centrifugal and Coriolis forces.
is the resultant inertial force. (pseudo force) which is the vector sum of centrifugal and Coriolis forces.
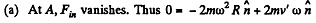
where 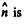 the inward drawn unit vector to the centre from the point in question, here A.
the inward drawn unit vector to the centre from the point in question, here A.
Thus, 
so, 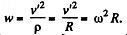
(b) At B 
its magnitude is 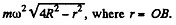
Q57: A small body of mass m = 0.30 kg starts sliding down from the top of a smooth sphere of radius R = 1.00 m. The sphere rotates with a constant angular velocity ω = 6.0 rad/s about a vertical axis passing through its centre. Find the centrifugal force of inertia and the Coriolis force at the moment when the body breaks off the surface of the sphere in the reference frame fixed to the sphere.
 View Answer
View Answer 
Ans. The equation of motion in the rotating coordinate system is,
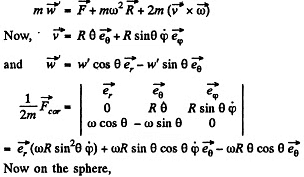
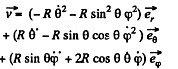
Thus the equation of motion are,
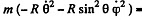
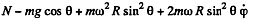
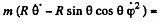
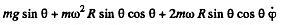
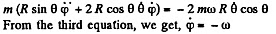
A result that is easy to understand by considering the motion in non-rotating frame. The eliminating φ we get,
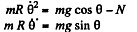
Integrating the last equation
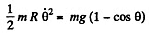
Hence
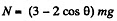
So the body must fly off for 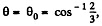 exactly as if the sphere were nonrotating.
exactly as if the sphere were nonrotating.
Now, at this point 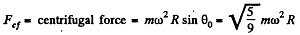
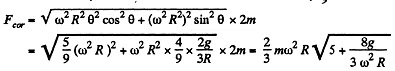
Q58: A train of mass m = 2000 tons moves in the latitude φ = 60° North. Find:
(a) the magnitude and direction of the lateral force that the train exerts on the rails if it moves along a meridian with a velocity v = 54 km per hour;
(b) in what direction and with what velocity the train should move for the resultant of the inertial forces acting on the train in the reference frame fixed to the Earth to be equal to zero.
 View Answer
View Answer 
Ans. (a) When the train is moving along a meridian only the Coriolis force has a lateral component and its magnitude (see the previous problem) is,
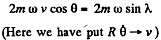
So, 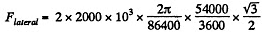
= 3.77 kN, (we write λ for the latitude)
(b) The resultant of the inertial forces acting on the train is,
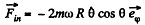
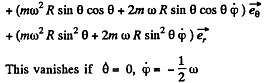
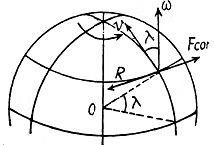
Thus 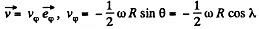
(We write λ for the latitude here)
Thus the train must move from the east to west along the 60th parallel with a speed,
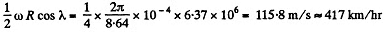
Q59: At the equator a stationary (relative to the Earth) body falls down from the height h = 500 m. Assuming the air drag to be negligible, find how much off the vertical, and in what direction, the body will deviate when it hits the ground.
 View Answer
View Answer 
Ans. We go to the equation given in 1.111. Here vy = 0 so we can take y = 0, thus we get for the motion in the 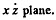 .
.
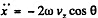
and 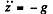
Integrating, 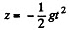

So 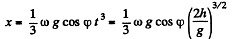
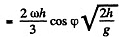
There is thus a displacement to the east of
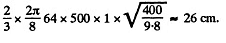
|
96 videos|367 docs|98 tests
|
FAQs on Irodov Solutions: The Fundamental Equation of Dynamics - Physics Class 11 - NEET
| 1. What is the fundamental equation of dynamics? |  |
| 2. How can I apply the fundamental equation of dynamics in problem-solving? |  |
| 3. What are the units used in the fundamental equation of dynamics? |  |
| 4. Can the fundamental equation of dynamics be applied to rotational motion? |  |
| 5. What common mistakes should I avoid when using the fundamental equation of dynamics? |  |

















