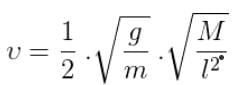Theory & Procedure, AC Sonometer | Physics Class 12 - NEET PDF Download
Our Objective:
To determine the frequency of alternating current using a sonometer.
The Theory:
A sonometer is an apparatus used to study the transverse vibrations of stretched strings. It is in the form of a hollow wooden rectangular box. On the wooden rectangular box there are two bridges and a pulley at one end. A wire string is attached to one end of the wooden box, run over the bridges and pulley and carries a weight hanger at the free end as shown in figure below.

A sonometer is used to determine the frequency of alternating current. A step down transformer is used for the determination of frequency of A.C. because the voltage of the A.C. mains is 220V, which is dangerous. The step down transformer reduces this voltage to 6 volts.
The string wire of the sonometer is a non-magnetic metallic wire like brass or copper. A horse shoe magnet is placed at the middle of the sonometer wire so that the magnetic field is applied perpendicular to the sonometer wire in a horizontal plane.
When an alternating current of definite frequency passes through the wire there will be interaction between the magnetic field and the current carrying conductor. So a force will act on the conductor in a direction perpendicular to both the field and the direction of current.
When A.C. is passing through the conductor, since the current direction reverses periodically, the direction of force also reverse periodically and hence, the conductor vibrates. Since the current flowing is alternating, the wire vibrates with a frequency equal to the frequency of A. C. By adjusting the length of the vibrating wire segment, this frequency can be made equal to the natural frequency of the wire segment. Then the resonance takes place and the wire vibrates with maximum amplitude. At this stage, the length of the wire segment is called the resonating length and it increases with increase in the mass of the suspended weights.

When the length ‘l’ of the sonometer wire vibrates with maximum amplitude, the frequency of the applied A.C. is equal to the natural frequency of the wire.

Where T = Mg, the tension of the wire and 'm' is the linear density of the wire.

If r is the radius of the wire, and ρ is the density of its material, m = πr²ρ
The graph between mass (M) of the suspended weights and square of the resonating length (l2) by taking M along X-axis and l2 along Y-axis is drawn. The graph should be a straight sloping line. The slope of the line AB/BC gives the value of M/l2, which is a constant.


Learning Outcomes:
- Students will be able to relate the tension of the wire, linear density of the wire and the resonating length of the wire.
- Students will be able to derive the relationship between frequency of alternating current and the resonating length of the wire.
Materials required:
- Sonometer
- Step down transformer
- Horse shoe magnet
- A set of slotted weights
- Weight hanger
- Paper rider
- Bridges
Real Lab Procedure:
- Place the sonometer on the table.
- Attach a weight hanger at the free end of the string which passes over the pulley.
- Stretch the wire by loading a suitable maximum mass on the weight hanger.
- The sonometer wire is connected to the secondary of the step down transformer.
- The horse shoe magnet is mounted at the middle of sonometer bed so as to produce a magnetic field perpendicular to the wire.
- The opposite poles of the magnet must face each other.
- The bridges are placed on either side of the magnet at equal distance from the magnet and are close to each other.
- A light paper rider is placed on the wire between the bridges of the sonometer.
- The A.C. supply is switched on.
- The wire begins to vibrate.
- The length of the wire between the two bridges is adjusted till the wire vibrates with maximum amplitude. At this stage, the paper rider placed on the wire is thrown off, which shows the condition of resonance.
- The length of the wire between the two bridges is measured. This is called the resonating length l.
- Then calculate the value of (M/l2).
- Repeat the experiment for different loads and the average value of (M/l2) is found.
- The linear density of the wire, m, can be calculated using the relation, m = πr2ρ, where r is the radius of the wire which can be measured using the screw gauge.
- By knowing the linear density, m, of the wire, the frequency of A.C. mains supply is calculated using the formula,

- Draw a graph between mass (M) of the suspended weights and square of the resonating length (l2) by taking M along X-axis and l2 along Y-axis. The graph should be a straight sloping line. The slope of the line gives the value of M/l2, which is a constant.
Simulator Procedure (as performed through the Online Labs)
- Select the environment from the drop down list.
- Select the material of the wire from the drop down list.
- Select the type of AC supply from the drop down list.
- Select the frequency of AC using the slider.
- Select the diameter of the wire using the slider.
- Select the weight of the slotted weights using the slider.
- Click on the ‘Power on’ to switch on/off the power supply.
- Change the position of bridge A using the slider.
- Change the position of bridge B using the slider.
- Change the position of the magnet using the slider.
- Click on the ‘Place the paper rider’ button to replace the paper rider.
- To redo the experiment, click on the ‘Reset’ button.
Find the diameter of the wire
1.To find the least count (L.C)
1 Linear Scale Division, LSD = 1 mm
Number of full rotations given to screw =4
Distance moved by the screw = 4mm
Hence, pitch p = 4mm/4 = 1mm
Number of divisions on circular scale=100
Hence, least count, L.C = 1mm/100 = 0.01 mm= 0.001 cm
2. Zero Error
(i) zero error = --------------mm
(ii) zero error = ---------------mm
(iii) zero error = ----------------mm
Mean zero error, e = ------------mm
Mean zero correction, c = -e = -------mm
Trial No. | PSR X(mm) | HSR a | Corrected HSR a ± c | Corrected HSR X L.C Y (mm) | Total reading X + Y (mm) | Mean Diameter mm (10-3m) |
Calculations:
The density of the material of the wire, ρ = ………………kg/m3
Radius of the wire r = ………..m
Linear density of the wire, m = πr2ρ = ………….kg/m
Mean (M/l2) = …………………. kg/m2
|
97 videos|336 docs|104 tests
|
FAQs on Theory & Procedure, AC Sonometer - Physics Class 12 - NEET
| 1. What is the theory behind the AC Sonometer? |  |
| 2. How does the AC Sonometer work? |  |
| 3. What is the procedure to perform an experiment using the AC Sonometer? |  |
| 4. What are the factors affecting the sound produced by the AC Sonometer? |  |
| 5. What are the applications of the AC Sonometer? |  |

|
Explore Courses for NEET exam
|

|