Screw Gauge | Physics and Measurement for NEET PDF Download
Using Vernier Calipers allows for accurate length measurements up to 0.1mm. However, for even finer measurements, down to 0.01mm or 0.005mm, a screw gauge surpasses Vernier Calipers in precision. In this document, we will study in detail the screw gauge and its usage followed by calculation techniques.
Purpose of Screw Gauge
- To measure the diameter of the given lead shot.
- To measure the diameter of a given wire and find its volume.
- To measure the thickness of a given glass plate and find its volume.
- To measure the volume of an irregular lamina.
The screw gauge is an instrument used for measuring accurately the diameter of a thin wire or the thickness of a sheet of metal. It consists of a U-shaped frame fitted with a screwed spindle which is attached to a thimble.
 Screw Gauge
Screw Gauge
Components of Screw Guage
- Parallel to the axis of the thimble, a scale graduated in mm is engraved. This is called the pitch scale. A sleeve is attached to the head of the screw.
- The head of the screw has a ratchet which avoids undue tightening of the screw.
- On the thimble, there is a circular scale known as head scale which is divided into 50 or 100 equal parts. When the screw is worked, the sleeve moves over the pitch scale.
- A stud with a plane end surface called the anvil is fixed on the ‘U’ frame exactly opposite to the tip of the screw. When the tip of the screw is in contact with the anvil, usually, the zero of the head scale coincides with the zero of the pitch scale.
- Pitch of the Screw Gauge
The pitch of the screw is the distance moved by the spindle per revolution. To find this, the distance advanced by the head scale over the pitch scale for a definite number of complete rotations of the screw is determined. The pitch can be represented as;
The pitch of the screw = Distance moved by screw/No. of full rotations given - Least Count of the Screw Gauge
The Least count (LC) is the distance moved by the tip of the screw when the screw is turned through 1 division of the head scale.
The least count can be calculated using the formula;
Least count = (Pitch/Total number of divisions on the circular scale) . - Zero Error and Zero Correction
To get the correct measurement, the zero error must be taken into account. For this purpose, the screw is rotated forward till the screw just touches the anvil and the edge of the cap is on the zero mark of the pitch scale. The Screw gauge is held keeping the pitch scale vertical with its zero downwards.
When this is done, any of the following three situations can arise:
(a) The zero mark of the circular scale comes on the reference line. In this case, the zero error and the zero correction, both are nil.
(b) The zero mark of the circular scale remains above the reference line and does not cross it. In this case, the zero error is positive and the zero correction is negative depending on how many divisions it is above the reference line.
(c) The zero mark of the head scale is below the reference line. In this case, the zero error is negative and the zero correction is positive depending on how many divisions it is below the reference line.

To find the diameter of the lead shot with the lead shot between the screw and anvil, if the edge of the cap lies ahead of the Nth division of the linear scale.
Then, linear scale reading (P.S.R.) = N.
If the nth division of the circular scale lies over the reference line.
Then, circular scale reading (H.S.R.) = n × (L.C.) (L.C. is the least count of screw gauge)
Total reading (T.R.) = P.S.R. + corrected H.S.R. = N + (n x L.C.).
If D is the mean diameter of the lead shot,
Then, the volume of the lead shot,
V = (4/3)π (D/2)3
To find the diameter and hence to calculate the volume of the wire
Place the wire between the anvil and the screw and note down the PSR and HSR as before.The diameter of the wire is given by;
T.R = PSR + (corrected HSR × L.C) = N + (n × L.C) ....(3)
If r is the radius of the wire, and l is the mean length of the wire.
Then, the volume of the wire,
V = π r2 I ....(4)
To find the thickness of the glass plate
The glass plate is gripped between the tip of the screw and the anvil. The PSR and HSR are noted as before.
The thickness of the glass plate is;
t = PSR + corrected HSR = N + (n × L.C) ....(5)
To find the Volume of glass plate (irregular lamina)
Find the thickness, t of irregular lamina as before. Then place the lamina over a graph paper and trace its outline on the graph paper. The area A of the lamina is taken from the graph paper.
The volume of the glass plate is calculated from the equation;
V = A ∗ t ........ (6)
SOLVED EXAMPLES
Example 1. What are the readings of the reading of the micrometer meter screw gauges as shown in the figures below?
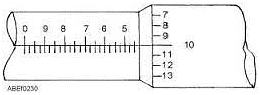
Solution. Reading of main scale = 4.50 mm
Reading of vernier scale = 10
Reading of Vernier scale x accuracy of Vernier caliper = 10 × 0.01 = 0.10 mm
Add the result of step III and step I to get the reading of the micrometer screw gauge.
= 4.50 + 0.10 = 4.60 mm
Reading of Vernier caliper = 4.60 mm
Example 2. What are the readings of the reading of the micrometer meter screw gauges as shown in the figures below?
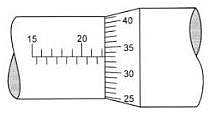
Solution. Reading of main scale = 22.0 mm
Reading of Vernier scale = 33
Reading of Vernier scale x accuracy of
Vernier caliper = 33 × 0.01 = 0.33 mm
Add the result of step III and step I to get the reading of the micrometer screw gauge.
= 22.0 + 0.33 = 22.33 mm
Reading of Vernier caliper = 22.33 mm
|
12 videos|27 docs|24 tests
|
FAQs on Screw Gauge - Physics and Measurement for NEET
| 1. What is the principle of a Screw Gauge? |  |
| 2. What is the purpose of a Screw Gauge? |  |
| 3. How is a Screw Gauge constructed? |  |
| 4. What is zero error in a Screw Gauge? |  |
| 5. What is the pitch of a Screw Gauge? |  |

|
Explore Courses for NEET exam
|

|


















