Theory & Procedure, Spherometer | Additional Study Material for NEET PDF Download
Objective
Our objectives are;
- To determine the thickness of a glass plate using a spherometer.
- To determine the radius of curvature of a given spherical surface using a spherometer.
Theory
A spherometer works on the principle of the micrometer screw. It is used to measure either very small thickness of flat materials like glass or the radius of curvature of a spherical surface thus getting its name.

Parts of a Spherometer
A spherometer consists of a metallic tripod framework supported on three fixed legs of equal lengths. A screw passes through the centre of the tripod frame, parallel to the three legs. A largeP)circular disc graduated with 100 equal parts is attached to the top of the screw. A small vertical scale known as the Pitch scale (P) with the scale reading divided into millimeters is fixed at one end of the tripod frame.
Thickness of a Glass Strip
The thickness of a glass strip can be represented by;
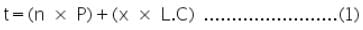
Where, 'n' is the number of complete rotation made by the circular disc.
'P' is the pitch, which is the distance moved by the middle screw per revolution.
'x' is the number of additional circular scale divisions in excess of complete rotations.
'L.C' is the least count of spherometer.
Least Count of the Spherometer
The pitch of the screw needs to be measured first. Find the value of 1 division on the pitch scale. Then bring the zero of the circular scale opposite to the pitch scale and rotate the screw by 'n' complete rotations. Note the distance 'd' moved by the screw on the pitch scale. The pitch of the screw is given by;
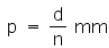
If there are N divisions in the circular scale on the circumference of the disc then;
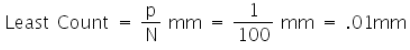
Measuring the Radius of Curvature of the Concave Surface
Let the figure represent the vertical section of the sphere of which the given surface forms a part, the vertical section passes through one of the outer legs 'A', the central screw 'G' and the centre of the sphere 'O'.The third leg 'C' is not visible.
Let , the height of central screw above the plane ABC, which is measured by the spherometer (h is called Sagitta.)
Learning Outcomes
- Students know the working of a spherometer.
- Students know the least count of spherometer.
- They know the equations for thickness of glass plate and radius of curvature of the concave surface.
Materials Required
- Spherometer
- Glass strip
- Concave surface
- Plane glass slab
- Glass strip
- A sheet of paper
- A ruler
- Pencil
Real Lab Procedure
To find the distance between the legs of the Spherometer
- Raise the central screw of the spherometer and press the spectrometer gently on a sheet of paper so as to get the pin pricks of the three legs. Mark these pricks as A, B and C.
- Measure the distance between the pricks by joining the points as to form a triangle.
- Note these distances (AB, BC, and AC) on the paper and take their mean as l.
To find the Least count of the Spherometer
- Note one pitch scale division on the pitch scale or vertical scale.
- Take 5 full rotations on the central screw.
- Measure the distance moved by the screw.
- Hence, Pitch = Distance moved /number of full rotations.
To find the radius curvature of the spherical surface
- Raise the screw sufficiently upwards.
- Place the spherometer on the concave surface so that its three legs rest on it.
- Gently turn the screw downwards till the screw tip just touches the concave surface.
- Note the reading of the circular disc scale which is in line with the vertical (pitch) scale. Note this reading as 'a', which will act as reference.
- Remove the spherometer from over the concave surface and place it over a large size glass slab.
- Turn the screw down wards and count the number of complete rotations made by the disc (one rotation becomes complete when the reference reading crosses past the pitch scale.)
- Continue till the tip of the screw just touches the plane surface of the glass slab.
- Note the reading of the circular scale which is finally in line with the vertical (pitch) scale. Note this reading as 'b'.
- Find the number of circular (disc) scale division in the last incomplete rotation.
- Now find total reading using the relation equation 1.
- Repeat steps 3 to 9, three times .Record the observation in tabular form.
- Calculate the radius of curvature of the given concave surface using the equation 2.
To find the thickness of the glass plate
- Raise the screw sufficiently upwards.
- Place the spherometer on the glass strip so that it rests between its three legs.
- Repeat the above steps 3 to 9, three times .Record the observation in a tabular form.
- Find total reading using the relation equation 1.
Simulator Procedure (as performed through the Online Labs)
- Click on the object shown on the left hand menu, to measure its thickness
- Tighten the screw by clicking on the respective arrows (left / right) on the screw, until it touches the object.
- Note the reading on pitch scale, the circular disc and note it down as the reference variable.
- Again click on the object on the left hand menu to remove it from under the spherometer.
- Tighten the screw by clicking on the respective arrows (left / right) on the screw, until it touches the glass slab.
- Note down the complete rotations on the pitch scale and note the reading on circular disc for fractional rotation.
- Based on the selected object;
- Calculate the radius of curvature if it is the spherical surface using the equation 2.
- calculate the thickness it it is the glass strip using the equation 1.
- Note down the reading in the text box.
- Click on the check button to find if the answer is correct.
- To redo the experiment, click on the 'Reset' button.
Calculation
The thickness of the glass plate, t = --------------- mm = --------------------m .
Mean value of h = -----------------------mm.
Radius of curvature of the spherical surface = ---------------cm=................m
Result
The thickness of glass strip = ------------m
The radius of curvature of the given concavesurface = -----------------m
|
26 videos|312 docs|64 tests
|
FAQs on Theory & Procedure, Spherometer - Additional Study Material for NEET
| 1. What is a spherometer and how does it work? |  |
| 2. What are the applications of a spherometer? |  |
| 3. How do you calibrate a spherometer? |  |
| 4. What are the sources of error in spherometer measurements? |  |
| 5. What is the difference between a spherometer and a profilometer? |  |

















