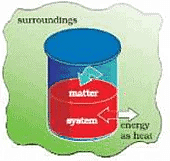
Thermodynamic Processes & Internal Energy | Physical Chemistry for NEET PDF Download
TYPES OF EQUILIBRIUM
(i) Thermal equilibrium → Equality of temperature
(ii) Mechanical equilibrium → Equality of pressure
(iii) Material equilibrium → no. of moles constant
When all the three equilibrium are established in a system, system is in true thermodynamics equilibrium.
THERMODYNAMIC PROCESSES
It is an operation by which a system undergoes a change from one state to another.
(i) Isothermal Process: A process in which the temperature remains constant throughout its course is called isothermal process.
i.e. ΔT = 0
(ii) Adiabatic Process: A process during which no heat is exchanged between the system and the surroundings is called adiabatic process.
i.e. dq = 0
(iii) Isobaric Process: A process in which pressure of the system remains constant is called isobaric process.
i.e. ΔP = 0
(iv) Isochoric Process: A process in which volume of the system remains constant is called isochoric process.
i.e. ΔV = 0
(v) Cyclic Process: System undergoes series of changes & ultimately comes back to initial state.
i.e., Δ U cyclic = 0; Δ H cyclic = 0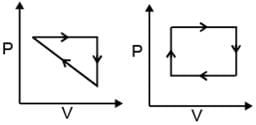
REVERSIBLE AND IRREVERSIBLE PROCESSES
Reversible process:
- A process that follows the reversible path, i.e., the process which occurs in infinite number of steps in this Way that the equilibrium conditions are maintained at each step, and the process can be reversed by infinitesimal change in the state of functions.
- If system & surrounding can restore their original state by reversing the direction of the process then process is called reversible process.
- In reversible process, there is no loss of energy.
- These are slow process as it takes infinite time. System & surrounding are always in equilibrium. Reversible process is a theoretical process. Reversible process is most efficient with respect to work.
- In reversible process Pext = Pint
Fig: Reversible & Irreversible Processes
Irreversible process: The process which cannot be reversed and amount of energy increases. All natural processes are Irreversible.
- Irreversible process is a fast process. It takes definite time for completion
- In irreversible process Pext ≠ Pint.
- It is an actual process. It is carried out in multiple stages and it tends towards reversible process.
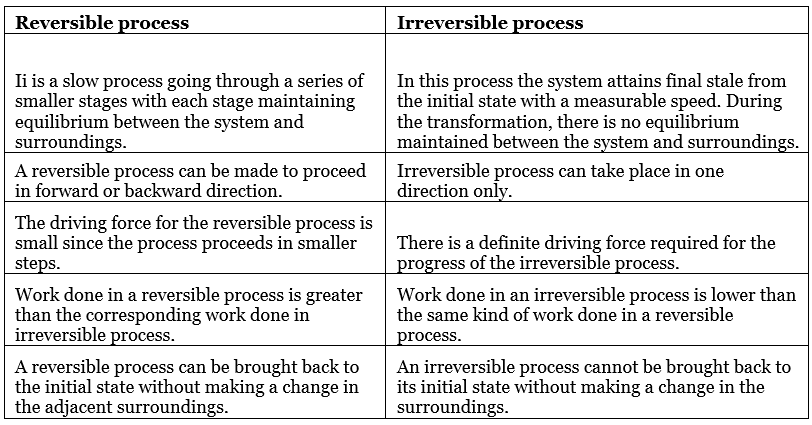
COMPARISON BETWEEN REVERSIBLE AND IRREVERSIBLE PROCESSES
INTERNAL ENERGY (E OR U)
- It is the total energy within the substance.
- It is the sum of many types of energies like vibrational energy, translational energy. etc.
- Energy (U) = TE + RE + VE + Chemical energy + nuclear energy + electron spin energy + PE
- U of the system, which may change, when
Heat passes into or out of the system,
Work is done on or by the system,
Matter enters or leaves the system. - It is an extensive property and state function.
- It is the change in internal energy accompanying a chemical or a physical process that is of interest and this is a measurable quantity.
- Its absolute value cannot be determined but experimentally change in internal energy (Δ) can be determined by
- ΔU = U2 – U1 or ΣUP – ΣUR
- Sign Convention:
➢ For exothermic process, ΔU = -ve , whereas
➢ for endothermic process ΔU = +ve U or E depends on temperature, pressure, volume and quantity of matter.
HEAT AND WORK
Heat & work both are forms of energy. Both are boundary phenomena and take place at the interface of the system & surroundings.
WORK
- Work is a mode, of energy transfer to or from a system with reference to the surroundings.
- If an object is displaced through a distance d x against a force of F, then the amount of work done is . defined as
W=F × dx
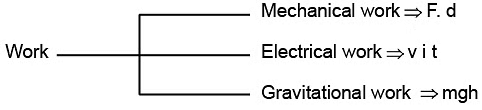
- Work associated with change in volume of a system against external pressure is called mechanical work.
Mechanical work = Pext (V2 - V1)= Pext ∆V
where, Pext = external pressure,
∆V increase or decrease in volume. - Work (w) is a path-dependent function.
- Work done on a system increases the energy of the system and work done by the system decreases the energy of the system.
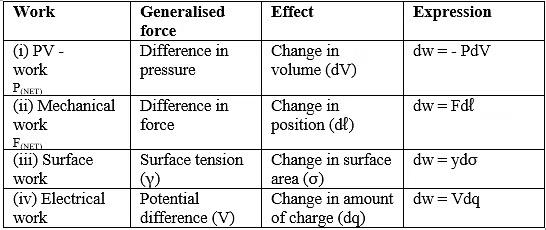
SIGN CONVENTION OF WORK DONE
Work done on the system, w = + ve
Work done by the system, w = -ve
Expansion: W ⇒ - ve
Compression: W ⇒ +ve
CHANGE IN INTERNAL ENERGY BY DOING WORK
We take a system containing some quantity of water in a thermos flask or in an insulated beaker.
The manner in which the state of such a system may be changed will be called adiabatic process.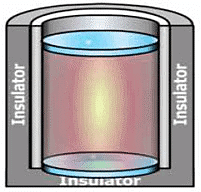
Let us call the initial state of the system as state 1 and its temperature as T1 . Let the internal energy of the system in state 1 be called U1.
We can change the state of the system by two different methods.
(i) First Method: By doing some mechanical work, say 1 kJ, by rotating a set of small paddles and thereby churning water. Let the new state be called 2 state and its temperature, as T2. It is found that T2 > T1 and the change in temperature, ∆T = T2 – T1. Let the internal energy of the system in state 2 be U2 and the change in internal energy, ∆U =U2 – U1.
(ii) Second Method: We now do an equal amount (i.e., 1kJ) electrical work with the help of an immersion rod and note down the temperature change.
 We find that the change in temperature is same as in the earlier case, say, ∆T = T2 – T1.
We find that the change in temperature is same as in the earlier case, say, ∆T = T2 – T1.
The internal energy U, whose value is characteristic of the state of a system, whereby the adiabatic work, wad required to bring about a change of state is equal to the difference between the value of U in one state and that in another state, ∆U i.e.,
∆U =U2 −U1
Therefore, internal energy, U, of the system is a state function.
CHANGE IN INTERNAL ENERGY BY TRANSFER OF HEAT
The energy that flows across the boundary of a system during a change in its state of difference in temperature between system and surroundings and flows from higher to lower temperature.
- We can bring about the same change in temperature by transfer of heat through thermally conducting walls which allows the heat to pass in and out of the walls.

- Let’s take water at temperature, T1 in a container made up of copper as it forms thermally conducting walls
- Enclose it in a huge heat reservoir at temperature, T2.
- The heat absorbed by the system (water), q can be measured in terms of temperature difference, T2 – T1.
- In this case change in internal energy, ∆U= q, when no work is done at constant volume.
SIGN CONVENTION OF HEAT
Heat given to the system from surroundings ⇒ +ve
Heat loss (it released) from the system to surroundings ⇒ - ve
SIGN CONVENTION
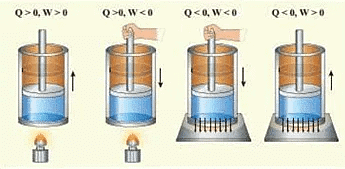
Since, heat and work are interrelated, S1 unit of heat is the joule(J).
I joule = 0.2390cal
1 calorie = 4.184 J
1 kcal =4.184 kJ
1 litre - atm =1 0 1.3 J
1.013 × 109 erg
= 24.206 cal
SOLVED EXAMPLES
Example 1. A gas expands by 0.5 litre against a constant pressure of one atmosphere. Calculate the work done in joule and calorie.
Sol.
Work = -Pext × Volume change
= −1 × 0.5=−0.5 L atm
= −0.5 × 101.328 J = −50.664 J
0.5 L atm = −0.5 × 24.20 cal = −12.10 cal
Example 2. One mole of an ideal gas is put through a series of changes as shown in the graph in which A, Band C mark the three stages of the system. At each stage the variables are shown in the graph ..
(a) Calculate the pressure at three stages of the system.
(b) Name the processes during the following changes:
(i) A to B
(ii) B to C
(iii) C to A and
(iv) overall change.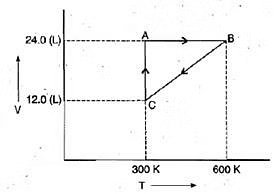 Sol.
Sol.
(a) At stage A:
V = 24.0 L
T = 300 K
N = 1
R = 0.0821 litre - atmK-1 mol-1
Substituting these values in the ideal gas equation, .
PV = nRT, At stage B: Volume remains the same but temperature changes from 300 K to 600 K. Thus, according to pressure law, the pressure will be doubled at B with respect to A.
At stage B: Volume remains the same but temperature changes from 300 K to 600 K. Thus, according to pressure law, the pressure will be doubled at B with respect to A.
Pressure at B= 2 × 1.026= 2.052 atm
At stage C: Temperature is 300 K and volume is half that of stage A. Thus, according to Boyle's law, the pressure at C will be doubled with respect to A.
Pressure at C = 2 × 1.026= 2.052 atm
(b) (i) During the change from A to B, volume remains constant, "'the process is isochoric.
(ii) During the change from B to C the pressure remains constant, the process is isobaric.
(iii) During the change from C to A, the temperature remains constant, the process is isothermal.
(iv) Overall; the process is cyclic as it returns to initial state.
Example 3. Calculate the work done when 1.0 mole; of water at 373 K vaporizes against an atmospheric pressure of 1.0 atmosphere. Assume ideal gas behaviour.
Sol. The volume occupied by water is very small and thus the volume change is equal to the volume occupied by one gram mole of water vapour.
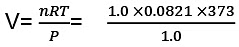 W=-Pext × ∆V
W=-Pext × ∆V
= -(1.0) × (31.0) litre-atm
= - (31.0) × 101.3 J = - 3140.3 J
|
117 videos|225 docs|239 tests
|
FAQs on Thermodynamic Processes & Internal Energy - Physical Chemistry for NEET
| 1. What is a thermodynamic process? |  |
| 2. What is internal energy in thermodynamics? |  |
| 3. How is internal energy related to the thermodynamic processes? |  |
| 4. Can internal energy be negative? |  |
| 5. How can the internal energy of a system be measured? |  |