Thermodynamic Variables and Equations of State | Chemistry Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Thermodynamic Equations of State |

|
| Osmotic Pressure and Osmotic Virial Coefficients |

|
| Solved Examples |

|
Introduction
A system is any part of the universe that is of interest to us. This might be the Sun-Earth-Moon system, a human lung, fruit fly, a single bacteria cell, or a beaker on a bench top. Some example systems are shown in Figure I.1.A:

Figure I.1.A: Some systems of varying complexity include the sun-earth-moon system, a human lung, a fruit fly, a single bacteria cell, or a beaker
- Everything else in the universe that is not part of the system is called the surroundings. The system + the surroundings constitutes the universe.
- We can classify systems into 3 types: open systems, closed systems, or isolated systems. An open system is able to exchange both matter and heat with the surroundings. A closed system cannot exchange matter with the surroundings but can exchange heat with the surroundings. An isolated system cannot exchange any heat or any matter with surroundings. These three types of systems are depicted in Figure I.1.B:
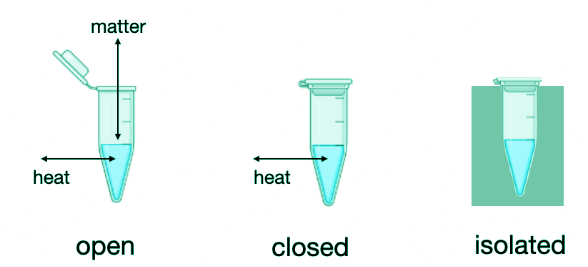
- The branch of science called thermodynamics is interested in the relationships between properties of a system and how properties change as the system changes state. A property is any mathematically quantifiable parameter of the system. Some properties could include the pressure, the temperature, the density, the index of refraction, etc ….
- We can distinguish between two types of properties: intensive and extensive. Intensive properties are independent of the quantity (amount of matter) being measured. Some intensive properties include the density, pressure, and temperature. On the other hand, Extensive properties depend on the quantity (amount) being measured. Some extensive properties are the mass, the volume, and the number of moles.
- Intensive properties can be constructed as the ratio between two extensive properties. For example the density is
Density = mass/volume (1.1.1) - Notice that both mass and volume are extensive (depend on the amount), but the density (the ratio of the mass over volume) is intensive. Similarly, the pressure is defined as
pressure = force/area (1.1.2) - The SI units of pressure is the Pascal (Pa) and 1 Pa = 1 N⋅m−2 = 1 kg⋅m−1⋅ s−2 = 1 J⋅m−3. Table I.1.i relates some common units of pressure.
- Table I.1.i: Some common units of pressure
1 Pa = 1 N m-2
1 bar = 100 kPa (105 Pa)
1 atm = 101.32 kPa
1 torr (mm Hg) = 1/760 atm
Note: Energy by itself (measured in Joules or calories) is an extensive property. Often, we report energies as a molar ratio in units of J/mol or cal/mol which is an intensive property.
- A common way to define an intensive property is to define the molar quantity by dividing some extensive variable by the number of moles. For example, the molar volume is defined as:
 (1.1.3)
(1.1.3) - Here n is the number of moles and V¯ is called the molar volume and is an intensive quantity.
Temperature is another important thermodynamic parameter that will be defined in serval ways throughout this text. For now, we will define the temperature as the measure of the motion of the atoms within the system. This definition of temperature implies that the “thermodynamic” temperature is measured in Kelvin, because the Kelvin scale is the absolute temperature scale. In the limit that T=0 K (absolute zero), the motion of the atoms approaches zero. We can convert between temperature in Kelvin and Celsius scales using the relation:
T(in Kelvins) = T(in∘C) + 273.15 (1.1.4)
Caution
Note: Absolute temperatures (in K) must be used in thermodynamic calculations.
Thermodynamic Equations of State
- An equation of state is a mathematical expression that fully describes the thermodynamic state of the system in terms of a set of physical properties. The most familiar example is the ideal gas law:
PV = nRT (1.1.5)
or, introducing the molar volume (Equation 1.1.3): (1.1.6)
(1.1.6) - where P is the pressure, V is the volume, n is the number of moles, T is the temperature. R is the gas constant given in Table I.1.ii. Equation 1.1.5 is known as the ideal gas equation of state. The ideal gas equation of state (PV=nRT) allows us to see how the properties of an ideal gas are related.
Table I.1.ii: Common units for the ideal gas constant R.
R = 8.314 J K-1 mol-1 = 0.08206 L atm K-1 mol-1 L atm = 101.34 J
- The ideal gas equation of state will be a useful model for us to work with as we derive thermodynamic relationships because it is intuitive and algebraically easy to manipulate. At this point, it is worthwhile to make some comments concerning the ideal gas equation of state:
The ideal gas equation of state can be derived from first principles (kinetic theory of gases).
- At sufficiently high temperature and low pressure, all gases fit the ideal gas law.
- Assumptions made in the ideal gas law:
- The gas molecules themselves occupy no volume.
- There are no attractive or repulsive forces between gas molecules.
- All collisions are perfectly elastic.
Because of these assumptions, we expect all real gases to deviate from ideal behavior. To quantify this we define the compressibility factor, Z, as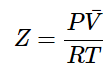
Notice from Equation 1.1.5 that for an ideal gas, Z = 1. All real gases will deviate from this ideal behavior. Figure I.1.C shows the compressibility factor Z as a function of pressure for N2 gas at different temperatures. A perfect ideal gas would have Z=1 for all pressures and temperatures. For N2 gas we see that at sufficiently low pressure Z→1 and that at higher temperature (purple curve), the gas behalves more like an ideal gas (dotted line).
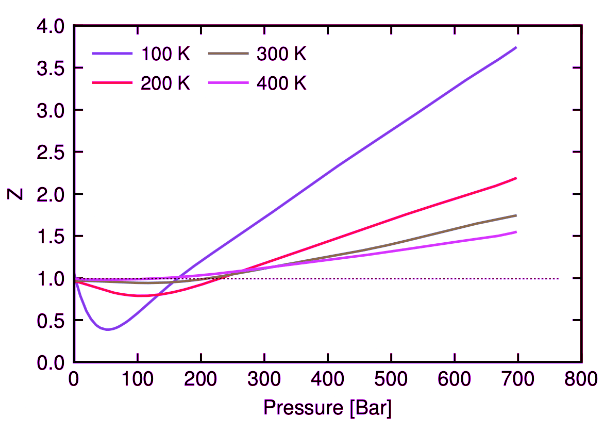
Figure I.1.C: Compressibility factor of nitrogen gas as a function of pressure for different temperatures. The ideal gas limit is shown by the dotted line at Z=1.
In order to derive an equation of state for a non-ideal gas, we can consider a series expansion of the compressibility factor, Z, in powers of the inverse molar volume, 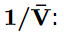
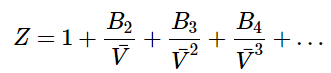 (1.1.8)
(1.1.8)
Equation 1.1.8 is called the virial equation of state, and B2 is called the second virial coefficient, B3 is called the third virial coefficient, etc…. The virial coefficients (B2, B3, …) are typically fit to experimental data and are temperature dependent. Notice that for a perfect ideal gas, the second and higher virial coefficients are all zero. The virial equation of state works well to describe any gas, but has the drawback of needing the virial coefficients from fitting to experimental data.
For gases that exhibit small deviations from ideal gas behavior, we can truncate Equation 1.1.8 to include just the second virial coefficient:
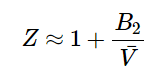 The second viral coefficient, B2 is related to the interactions between atoms described by a potential energy function U(r), where r is the distance between atom pairs. For a dilute system of non-polar molecules, the relationship between the second virial coefficient and the potential energy is
The second viral coefficient, B2 is related to the interactions between atoms described by a potential energy function U(r), where r is the distance between atom pairs. For a dilute system of non-polar molecules, the relationship between the second virial coefficient and the potential energy is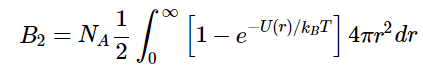 where NA is Avogadro’s number, kB is Boltzmann’s constant, and T is the temperature. In most cases, we cannot analytically solve the integral in Equation 1.1.10. Note that in the absence of interactions, U(r) = 0, then from Equation 1.1.10, B2 = 0 and the gas behaves like an ideal gas as we would expect for non-interacting gas molecules.
where NA is Avogadro’s number, kB is Boltzmann’s constant, and T is the temperature. In most cases, we cannot analytically solve the integral in Equation 1.1.10. Note that in the absence of interactions, U(r) = 0, then from Equation 1.1.10, B2 = 0 and the gas behaves like an ideal gas as we would expect for non-interacting gas molecules.
[Question: 949623]
Osmotic Pressure and Osmotic Virial Coefficients
- In dealing with solutions (either solutions of small molecule solutes or macromolecules in solution), an important colligative property is the osmotic pressure. The osmotic pressure is given by the symbol Π and is different from the pressure of a gas (P) because it does not arise from collisions of molecules against the wall of a container. The osmotic pressure is a hydrostatic pressure that arises when solvent molecules pass through a semipermeable membrane to the more concentrated side of the membrane as shown in Figure I.1.D.
- The flow of solvent across the semipermeable membrane is called osmosis. Consider the osmotic pressure (Π) that develops on the more concentrated side of the membrane due to solvent molecules moving from the dilute to the concentrated side of the membrane. This situation illustrated in Figure I.1.D.
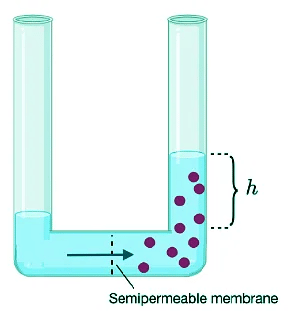
Figure I.1.D: Definition of osmotic pressure. The difference in concentration across the membrane causes a chemical potential. Solvent flows from the dilute to the concentrated side in an attempt to equalize the chemical potential. As water flows from the dilute to concentrated side, the water level will rise on the concentrated side. At equilibrium, the pressure differential is equal to the osmotic pressure.
- As the pressure builds up on the high concentration side, the solvent level will rise by a height, h. The hydrostatic pressure is the difference between the pressure on the two sides of the semipermeable membrane and is given as
Π = ρgh (1.1.11) - where ρ is the solvent density, and g is the acceleration due to gravity. For an ideal solution, the osmotic pressure, Π, resembles the form of the ideal gas law:
ΠV = nRT (1.1.12)
Using the fact that n/V is the concentration (i.e. number of moles per unit volume of solution), we can rewrite Equation 1.1.12 in terms of the molarity (M): (1.1.13)
(1.1.13) - If we define the mass concentration (C) of the solute (in units of g • L-1), then we can rewrite 1.1.13 as:
 (1.1.14)
(1.1.14) - where Mw is the molar mass of the solute molecule (in units of g • mol-1), and C is the mass concentration of the solute ( C=nMw/V).
- Equation 1.1.14 assumes we are dealing with an ideal solution in which the solute particles are non-interacting. Instead, if we want to consider a non-ideal solution of weakly interacting molecules, we can expand Equation 1.1.14 in powers of C to obtain a virial equation of state for the osmotic pressure of a real solution: (1.1.15)
 where B′2, B′3, B′4... are the second, third, and fourth osmotic virial coefficients.
where B′2, B′3, B′4... are the second, third, and fourth osmotic virial coefficients.
In the dilute limit (C << 1), we can truncate the expansion at the second virial coefficient: (1.1.16)
(1.1.16)- The second virial coefficient B′ is related to the interactions between atoms describe by the potential energy function U(r) through the relation given above in Equation 1.1.10. The second virial coefficent may be positive or negative depending on the nature of the particle-particle interactions. A negative coefficient corresponds to net attractive interactions, and a positive coefficient correspond to repulsive interactions.
Note: The second virial coeffient, B′2, as written in Equation 1.1.16 is related to the second virial coefficients, B2, in Equation 1.1.9 by the relation: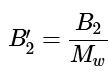 (1.1.17)
(1.1.17)
- Osmotic pressure plays an important role in biology. For example, trees use osmotic pressure to transport water from the roots to the upper branches. The effect of osmotic pressure on the cell is illustrated in Figure I.1.E. When red blood cells are placed in a salt solution having a lower concentration than the intracellular fluid, the solution is hypotonic, and the cell will gain water through osmosis in an attempt to equalize the osmotic pressure. This situation is illustrated in Figure I.1.E (a).
- The cells will swell and potentially burst. When red blood cells are placed in a salt solution with the same osmotic pressure as the intracellular fluid, the solution is isotonic with respect to the cytoplasm. This situation is illustrated in See Figure I.1.E (b). Finally, when red blood cells are placed in a solution with a higher salt concentration than the intracellular fluid, the solution is hypertonic and water inside the cell flows outside the cell in an attempt to equalize the osmotic pressure, causing the cell to shrink. This is the situation illustrated in Figure I.1.E (c).
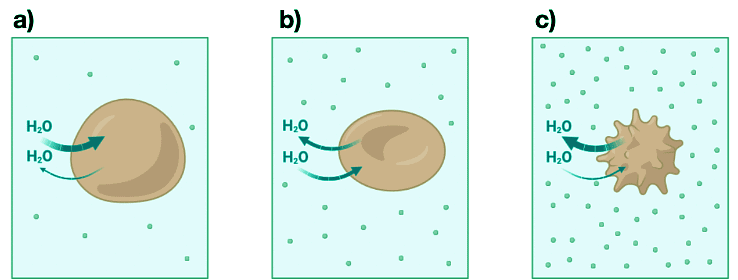
Figure I.1.E: a) When red blood cells are placed in a hypotonic solution whose osmotic pressure is less than that of the intracellular fluid, water flows into the cells and the cell swells and eventually bursts. b) When red blood cells are placed in an isotonic salt solution having the same osmotic pressure as the intracellular fluid, the rate of flow of water into and out of the cells is the same and the cell does not change shape. c) When red blood cells are placed in a hypertonic solution, the osmotic pressure is greater outside than that of the intracellular fluid, and water flows out of the cells. The cells shrink.
Solved Examples
Example 1: Classify each of the following systems as either open, closed, or isolated. (a) A red blood cell, (b) a gas in a piston without valves, (c) boiling water in a kettle on the stove, (d) A closed Thermos flask of hot coffee (approximately).
Ans: (a) open; (b) closed; (c) open; (d) isolated
Example 2: A Bellingham homebrewer collects the amount of gas evolved during the fermentation process. Later, the brewer measures the volume of gas to be 0.64 L at a cold temperature of 12.3 °C and 1 atm. Assuming ideal gas behavior, what was the volume of the gas at the fermentation temperature of 37.0 °C and 1 atm.
Ans: We use the ideal gas equation: PV=nRT to set up a ratio between the low temperature and high temperature system:
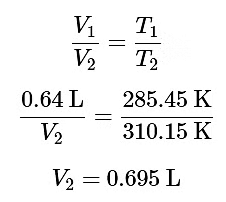

|
Explore Courses for UPSC exam
|

|
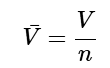 (1.1.3)
(1.1.3)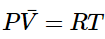 (1.1.6)
(1.1.6)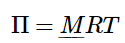 (1.1.13)
(1.1.13)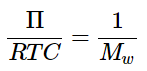 (1.1.14)
(1.1.14)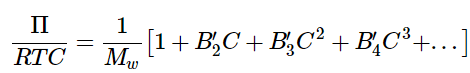 where B′2, B′3, B′4... are the second, third, and fourth osmotic virial coefficients.
where B′2, B′3, B′4... are the second, third, and fourth osmotic virial coefficients.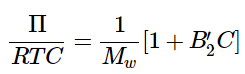 (1.1.16)
(1.1.16)















