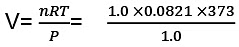Thermodynamics: Common Terms, State Function, Reversible & Irreversible Processes | Chemistry Class 11 - NEET PDF Download
| Table of contents |

|
| What is Thermodynamics? |

|
| The System and the Surroundings |

|
| Basic Thermodynamic Terms |

|
| Thermodynamic Processes |

|
| Reversible and Irreversible Processes |

|
| Laws of Thermodynamics |

|
Thermodynamics is about understanding how heat and energy work. It looks at how different types of energy can change from one form to another. There are three main rules that explain how energy behaves. The term "thermodynamics" was made up by William Thomson in 1749. Let's now explore some basic terms you'll come across in thermodynamics.
 Examples of Energy Transformation
Examples of Energy Transformation
What is Thermodynamics?
The branch of chemistry that deals with the movement of energy from one form to the other and the relation between heat and temperature with energy and work done is called thermodynamics.
Molecules store chemical energy, which can be liberated as heat when fuels such as methane, cooking gas, or coal undergo combustion in the presence of air. This released energy can be harnessed to perform mechanical work in engines or converted into electrical energy through devices like dry cells.
The diverse forms of energy are interconnected, and under specific circumstances, they can transform from one form into another. Thermodynamics is the field that explores and analyzes these energy transformations.
Note: Thermodynamics as the science stream that deals with the study of the combined effects of heat and work on the changes in the state of matter confined by the laws of thermodynamics.
What is the Use of Thermodynamics?
- Feasibility of a process: It helps to lay down the criteria for predicting the feasibility or spontaneity of a process, including a chemical reaction, under a given set of conditions.
- The extent of a process: It helps to determine the extent to which a process, including a chemical reaction, can proceed before the attainment of equilibrium.
- The efficiency of a process: The study of thermodynamics is based on three generalizations derived from experimental results. These generalizations are known as the first, second, and third laws of thermodynamics based on human experience and there is no formal proof for them.
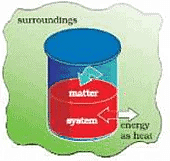
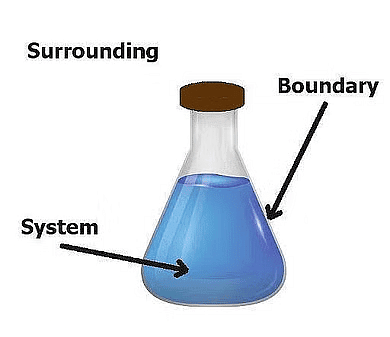
The System and the Surroundings
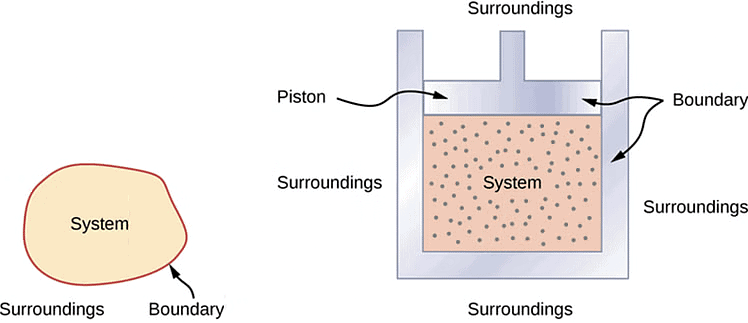
1. System
A thermodynamic system is defined as a quantity of matter or a region in space that is of interest. A system can exchange exclusively mass, exclusively energy, or both mass and energy with its surroundings.
 System, Surrounding, and Boundary
System, Surrounding, and Boundary
2. Surroundings
The surroundings contain everything other than the system. The system and the surroundings together make up the universe. A thermodynamic system is embedded in its environment or surroundings, through which it can exchange heat with, and do work on
3. Boundary
The part that separates the system and surroundings is called the boundary it may be rigid or flexible. It may be diathermic (able to conduct heat or pass heat freely)or adiabatic (there is no heat transfer from in or out of the system).
System + Boundary + Surrounding = Universe
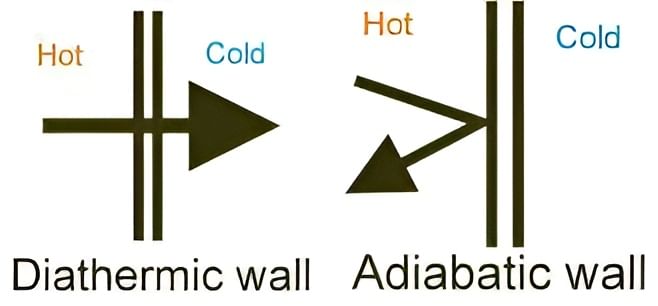 Difference in Diathermic and Adiabatic Wall
Difference in Diathermic and Adiabatic Wall
The boundary may be real or imaginary; it may be rigid or non-rigid; it may be a conductor or a non-conductor of heat.
 System Thermodynamics
System Thermodynamics
Types of System
1. Open systemThe system can exchange matter as well as energy with the surroundings.
Example: a liquid kept in an open flask.
 Open System
Open System
2. Closed System
A system that can exchange only energy with the surroundings.
Example: A liquid in a closed vessel.
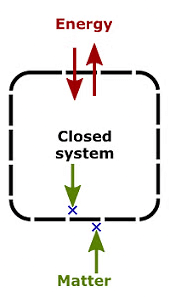 Closed System3. Isolated System
Closed System3. Isolated System
A system that can neither exchange matter nor energy with the surroundings.
Example: a thermally insulated flask.
 Isolated System
Isolated System
State and Path Functions
(i) State Function
A property whose value doesn’t depend on the path taken to reach that specific value is known to as a state function or point function.
 Representation of State Functions
Representation of State Functions
- When macroscopic properties of a system have definite values, the system is said to be in an indefinite state.
- Whenever there is a change in any one of the macroscopic properties, the system is said to change into a different state.
Thus, the state of a system is fixed by its macroscopic properties.
State Variables
The state or condition of a system is described by certain measurable properties & these measurable properties are called state variables.
 State Variables
State Variables
State variables or the thermodynamics parameters depend only upon the initial and final states of the system and are independent of how the change is brought are called state functions.
Note: State function depends only on the initial & final state of the system. It does not depend on the path or how the process was carried out.
Some common state functions are internal energy, enthalpy, entropy, free energy, pressure, temperature, volume, etc. The explanation for some of them is listed below:
- Pressure: Pressure is a measure of the average force exerted by the constituent molecules per unit area on the container walls. Pressure does not depend on the path of the molecules and thus it is a state function.
- Temperature: Temperature is defined as the measure of the average kinetic energy of the atoms or molecules in the system. Temperature measures a property of a state of a system irrespective of how it got there and thus it is a state function.
- Volume: Volume is the amount of physical space occupied by a substance and it will not be dependent on the path followed. Thus, the volume is a state function
- Mass: The measure of the amount of matter in an object is known as mass and is usually measured in grams (g) or kilograms (kg). Mass measures the quantity of matter regardless of both its location in the universe and the gravitational force applied to it and thus it is a state function.

- Internal energy: It can be defined as the sum of all kinds of energy associated with molecular motions.
The internal energy of ideal gases is a function of temperature only (Joule’s law) and the internal energy of real gases is a function of temperature, pressure, and volume (temperature and volume being the dominating quantities, and the effect of pressure are negligible), So it can be seen that since internal energy depends on quantities like P, T, V which are state functions, the internal energy is also a state function. - Gibb’s free energy: The enthalpy of the system at any point minus the product of the temperature times the entropy of the system is Gibb’s free energy of the system
G = H – TS
The Gibbs free energy of the system is a state function because it is defined in terms of thermodynamic properties that are state functions. - Entropy: Entropy is the measure of imbalance in the system and it’s totally independent of the path through which the system has achieved that state also it’s unique to the current state of the system
(ii) Path Functions
Path function depends on the initial as well as the final state of a system & also depends on the path of the process. Example: heat and work.
- Different paths give different values of the system.
- Path function requires multiple integrals and limits of integration to integrate the property
- Depends on the specific process or path and work, Heat and other energy transfer forms.
Basic Thermodynamic Terms
(a) Internal Energy
It refers to the energy contained within the system. The energy represents the overall energy of the system and may include many forms of energy such as potential energy, kinetic energy, etc. In a chemical reaction, we know about energy transformations and basic thermodynamics provides us with information regarding energy change associated with the particles of the system.
- It is the total energy within the substance.
- It is the sum of many types of energies like vibrational energy, translational energy. etc.
Energy (U) = TE + RE + VE + Chemical energy + nuclear energy + electron spin energy + PE
U of the system, which may change, when
Heat passes into or out of the system,
Work is done on or by the system,
Matter enters or leaves the system.
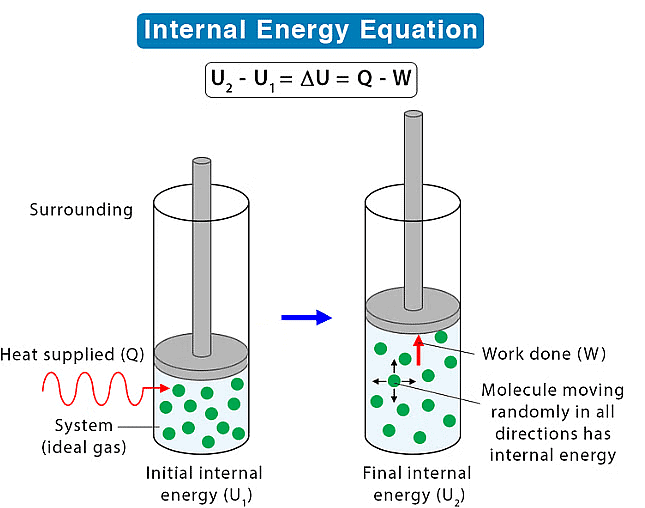 Representation of Internal Energy
Representation of Internal Energy
- It is an extensive property and state function.
- It is the change in internal energy accompanying a chemical or a physical process that is of interest and this is a measurable quantity.
- Its absolute value cannot be determined but experimentally change in internal energy (Δ) can be determined by ΔU = U2 – U1 or ΣUP – ΣUR
Sign Convention for Internal Energy
➢ For exothermic process, ΔU = -ve , whereas
➢ for endothermic process ΔU = +ve
U or E depends on temperature, pressure, volume and quantity of matter.
Factors Affecting the Internal Energy
The internal energy of a system may change when:
(a) Heat passes into or out of the system.
(b) Work is done on or by the system or matter enters or leaves the system.
(b) Work
Work done by a system is defined as the quantity of energy exchanged between a system and its surroundings. Work is completely governed by external factors such as an external force, pressure or volume, change in temperature, etc.

- Work is a mode, of energy transfer to or from a system with reference to the surroundings.
- If an object is displaced through a distance d x against a force of F, then the amount of work done is . defined as
W=F × dx
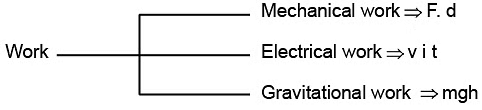
- Work associated with change in volume of a system against external pressure is called mechanical work.
Mechanical work = Pext (V2 - V1)= Pext ∆V
where, Pext = external pressure,
∆V increase or decrease in volume. - Work (w) is a path-dependent function.
- Work done on a system increases the energy of the system and work done by the system decreases the energy of the system.
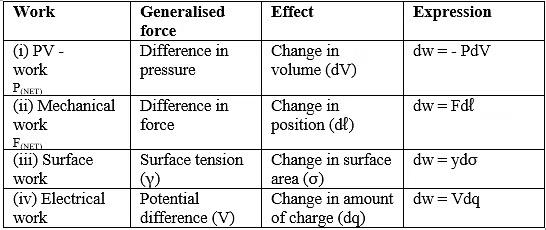
Sign Convention of Work Done
Work done on the system => w = + ve
Work done by the system => w = -ve
Expansion: W ⇒ - ve
Compression: W ⇒ +ve
(c) Heat
Heat in thermodynamics is defined as the kinetic energy of the molecules of the substance.
 Change in internal energy formula
Change in internal energy formula
- Heat and thermodynamics together form the basics which helped process designers and engineers to optimize their processes and harness the energy associated with chemical reactions economically.
- Heat energy flows from higher temperature to lower temperature.
Change in Internal Energy by doing Work
We take a system containing some quantity of water in a thermos flask or in an insulated beaker.
The manner in which the state of such a system may be changed will be called adiabatic process.
Let us call the initial state of the system as state 1 and its temperature as T1 . Let the internal energy of the system in state 1 be called U1.
We can change the state of the system by two different methods.
(i) First Method: By doing some mechanical work, say 1 kJ, by rotating a set of small paddles and thereby churning water. Let the new state be called 2 state and its temperature, as T2. It is found that T2 > T1 and the change in temperature, ∆T = T2 – T1. Let the internal energy of the system in state 2 be U2 and the change in internal energy, ∆U =U2 – U1.
(ii) Second Method: We now do an equal amount (i.e., 1kJ) electrical work with the help of an immersion rod and note down the temperature change.

We find that the change in temperature is same as in the earlier case, say, ∆T = T2 – T1.
The internal energy U, whose value is characteristic of the state of a system, whereby the adiabatic work, wad required to bring about a change of state is equal to the difference between the value of U in one state and that in another state, ∆U i.e.,
∆U =U2 −U1
Therefore, internal energy, U, of the system is a state function.
Change in Internal Energy by transfer of Heat
The energy that flows across the boundary of a system during a change in its state of difference in temperature between system and surroundings and flows from higher to lower temperature.
- We can bring about the same change in temperature by transfer of heat through thermally conducting walls which allows the heat to pass in and out of the walls.

- Let’s take water at temperature, T1 in a container made up of copper as it forms thermally conducting walls
- Enclose it in a huge heat reservoir at temperature, T2.
- The heat absorbed by the system (water), q can be measured in terms of temperature difference, T2 – T1.
- In this case change in internal energy, ∆U= q, when no work is done at constant volume.
Types of Equilibrium
(i) Thermal equilibrium → Equality of temperature
(ii) Mechanical equilibrium → Equality of pressure
(iii) Material equilibrium → no. of moles constant
When all the three equilibrium are established in a system, system is in true thermodynamics equilibrium.
Thermodynamic Processes
It is an operation by which a system undergoes a change from one state to another.
(i) Isothermal Process: A process in which the temperature remains constant throughout its course is called isothermal process.
i.e. ΔT = 0
(ii) Adiabatic Process: A process during which no heat is exchanged between the system and the surroundings is called adiabatic process.
i.e. dq = 0
(iii) Isobaric Process: A process in which pressure of the system remains constant is called isobaric process.
i.e. ΔP = 0
(iv) Isochoric Process: A process in which volume of the system remains constant is called isochoric process.
i.e. ΔV = 0
(v) Cyclic Process: System undergoes series of changes & ultimately comes back to initial state.
i.e., Δ U cyclic = 0; Δ H cyclic = 0
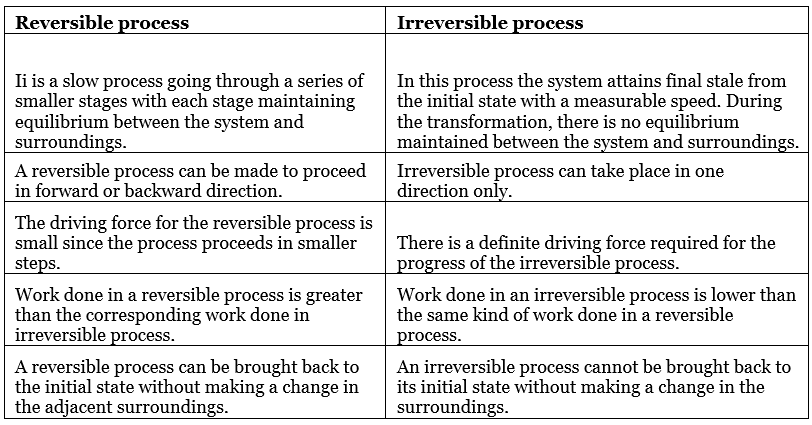
Reversible and Irreversible Processes
1. Reversible process
- A process that follows the reversible path, i.e., the process which occurs in infinite number of steps in this Way that the equilibrium conditions are maintained at each step, and the process can be reversed by infinitesimal change in the state of functions.
- If system & surrounding can restore their original state by reversing the direction of the process then process is called reversible process.
- In reversible process, there is no loss of energy.
- These are slow process as it takes infinite time. System & surrounding are always in equilibrium. Reversible process is a theoretical process. Reversible process is most efficient with respect to work.
- In reversible process Pext = Pint
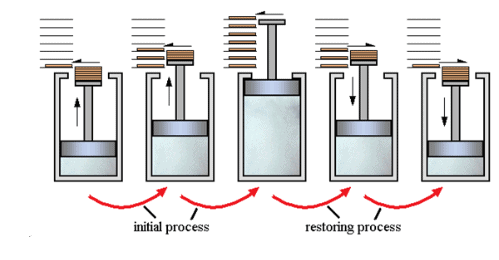 Reversible & Irreversible Processes
Reversible & Irreversible Processes
2. Irreversible process
The process which cannot be reversed and amount of energy increases. All natural processes are Irreversible.
- Irreversible process is a fast process. It takes definite time for completion
- In irreversible process Pext ≠ Pint.
- It is an actual process. It is carried out in multiple stages and it tends towards reversible process.
Comparision Between Reversible and Irreversible Processes
Laws of Thermodynamics
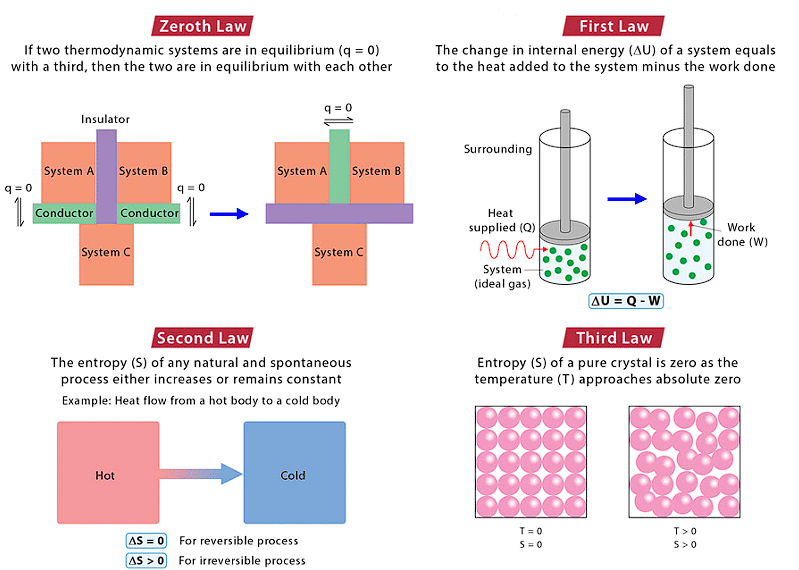
Important: Laws of thermodynamics apply only when a system is in equilibrium or moves from one equilibrium state to another equilibrium state.
- The Zeroth law of thermodynamics states that if two bodies are each in thermal equilibrium with some third body, then they are also in equilibrium with each other.
- The first law of thermodynamics: When energy moves into or out of a system, the system’s internal energy changes by the law of conservation of mass.
- The second law of thermodynamics: The state of the entropy of the entire universe, as an isolated system, will always increase over time.
- Third law of thermodynamics: Entropy of a perfect crystal at absolute zero is zero.
 Laws of Thermodynamics
Laws of Thermodynamics
Intensive and Extensive Properties

Intensive and extensive properties are characteristics used to describe the physical properties of substances in the fields of physics and chemistry. The terms intensive and extensive were first described by physicist Richard C. Tolman in 1917.
Intensive Properties:
- Intensive properties are those that do not depend on the amount of substance present. Examples include temperature, density, and color. These characteristics remain constant regardless of the quantity of the substance.
Extensive Properties:
- Extensive properties, on the other hand, do depend on the amount of substance present. Examples include mass, volume, and energy. These properties change as the quantity of the substance changes.
What Are Intensive Properties?
Intensive properties are bulk properties, which means they do not depend on the amount of matter that is present. Examples of intensive properties include:
- Boiling Point
- Density
- State of Matter
- Color
- Melting Point
- Odor
- Temperature
- Refractive Index
- Luster
- Hardness
- Ductility
- Malleability
- Each of these qualities remains the same for a substance no matter its quantity. Regardless of whether you have two or 2,000 liters of water, for example, the boiling point will always remain 100 degrees Celsius.
What Are Extensive Properties?
Extensive properties do depend on the amount of matter that is present. An extensive property is considered additive for subsystems. Examples of extensive properties include:
- Volume
- Mass
- Size
- Weight
- Length
- Energy
The ratio between two extensive properties is an intensive property. For example, mass and volume are extensive properties, but their ratio (density) is an intensive property of matter.
Way to Tell Intensive and Extensive Properties Apart:
One easy way to tell whether a physical property is intensive or extensive is to take two identical samples of a substance and put them together. If this doubles the property (e.g., twice the mass, twice as long), it's an extensive property. If the property is unchanged by altering the sample size, it's an intensive property.
Understanding whether a property is intensive or extensive is crucial for characterizing and identifying substances accurately in science.
Intensive vs. Extensive Properties
- The two types of physical properties of matter are intensive properties and extensive properties.
- Intensive properties do not depend on the quantity of matter. Examples include density, state of matter, and temperature.
- Extensive properties do depend on sample size. Examples include volume, mass, and size.
Some Important Questions
Q1:Give examples of state functions.
Ans: Examples of state functions are:
Pressure
Mass
Temperature
Enthalpy
Internal energy
Entropy
Volume
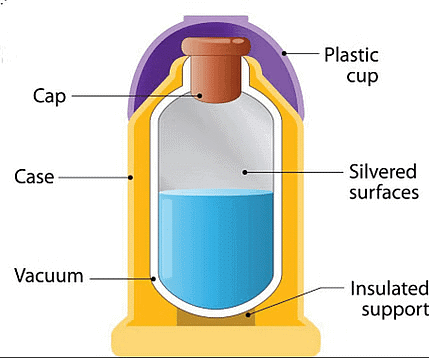
Q2: Thermos flask is a ______
Diathermic system
Only closed system
Isolated system
Only adiabatic system
Ans: Isolated System
Solution: Thermos flask is an Isolated system. It is a type of insulating storage vessel that keeps a hotter or cooler item at its respective temperature for a long time is called a thermos flask. So, the Thermos flask is an Isolated system.
 Thermos Flask
Thermos Flask
Q3: In thermodynamics, heat, and work are :
Point functions
Extensive thermodynamic state variables
Path functions
Intensive thermodynamic state variables
Ans: Heat and work are Path Functions
Solution: Path functions:
Path functions are defined as the thermodynamical variables that depend on the way/path in which the thermodynamical system achieves the initial and final states.
The differential of path functions is inexact.
Heat, work, and entropy generation are path functions.
Point functions:
Path functions are defined as the thermodynamic variable that depends on end states only i.e. initial and final states. They do not depend upon the path followed.
The differential of point functions is exact.
Pressure, temperature, volume, entropy, enthalpy, energy, etc are point functions.
Q4: Spot the odd one out
1. Specific enthalpy
2. Kinetic Energy
3. Work
4. Pressure
Ans: Option 3: work
Solution: The thermodynamic properties which depend on the end states, as well as the path followed, are known as path functions like heat and work.
Q5: Which of the following is an intensive property of a thermodynamic system?
1. Temperature
2. Mass
3. Energy
4. Volume
Ans: Option 1: temperature
Solution: Here is the difference between the two properties:
Q6: The total number of intensive properties from the following is __________ Volume, Molar heat capacity, Molarity, Eθ cell, Gibbs free energy change, Molar mass, Mole.
Ans: 4
Solution: Intensive properties are independent of the amount of the substance. They don't change with the size or mass of a sample. Examples include temperature, pressure, density, and concentration.
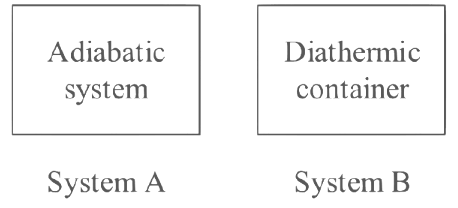
Q7: What happens when methane undergoes combustion in systems A and B respectively?
 (a) System A: Temperature Falls & System B: Temperature Rises
(a) System A: Temperature Falls & System B: Temperature Rises
(b) System A: Temperature Rises & System B: Temperature remain same
(c) System A: Temperature Falls & System B: Temperature remain same
(d) System A: Temperature remain same & System B: Temperature Rises
Ans: (b)
Solution: When methane undergoes combustion in systems ! (adiabatic system) and B (diathermic container), the outcomes are as follows:
- System A (adiabatic system): In an adiabatic system, no heat exchange occurs between the system and its surroundings. As methane undergoes combustion, which is an exothermic process, the heat generated by the reaction is retained within the system, causing the temperature to rise. Therefore, for System A, the temperature rises.
- System B (diathermic container): In a diathermic container, heat exchange is allowed between the system and its surroundings. !s methane undergoes combustion, the heat generated by the reaction is partially transferred to the surroundings. Depending on the heat capacity of the container and the extent of heat transfer, the temperature of the system may rise, remain the same, or even fall. However, in most cases, the temperature in System B would be expected to rise, but at a slower rate compared to System A.
Based on this information, the most appropriate option is:
System A: Temperature rises
System B: Temperature remains same
Q8: Among the following the number of state variables is __________.
Internal energy (U), Volume (V), Heat (q) and Enthalpy (H)
Ans: 3
Solution: State variables are internal energy (U), Volume (V) and Enthalpy (H).
Example 9. A gas expands by 0.5 litre against a constant pressure of one atmosphere. Calculate the work done in joule and calorie.
Sol.
Work = -Pext × Volume change
= −1 × 0.5=−0.5 L atm
= −0.5 × 101.328 J = −50.664 J
0.5 L atm = −0.5 × 24.20 cal = −12.10 cal
Example 10. One mole of an ideal gas is put through a series of changes as shown in the graph in which A, Band C mark the three stages of the system. At each stage the variables are shown in the graph .
(a) Calculate the pressure at three stages of the system.
(b) Name the processes during the following changes:
(i) A to B
(ii) B to C
(iii) C to A and
(iv) overall change.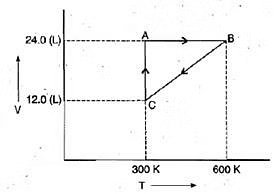
Sol. (a) At stage A:
V = 24.0 L
T = 300 K
N = 1
R = 0.0821 litre - atmK-1 mol-1
Substituting these values in the ideal gas equation, .
PV = nRT,
At stage B: Volume remains the same but temperature changes from 300 K to 600 K. Thus, according to pressure law, the pressure will be doubled at B with respect to A.
Pressure at B= 2 × 1.026= 2.052 atm
At stage C: Temperature is 300 K and volume is half that of stage A. Thus, according to Boyle's law, the pressure at C will be doubled with respect to A.
Pressure at C = 2 × 1.026= 2.052 atm
(b) (i) During the change from A to B, volume remains constant, "'the process is isochoric.
(ii) During the change from B to C the pressure remains constant, the process is isobaric.
(iii) During the change from C to A, the temperature remains constant, the process is isothermal.
(iv) Overall; the process is cyclic as it returns to initial state.
Example 11. Calculate the work done when 1.0 mole; of water at 373 K vaporizes against an atmospheric pressure of 1.0 atmosphere. Assume ideal gas behaviour.
Sol. The volume occupied by water is very small and thus the volume change is equal to the volume occupied by one gram mole of water vapour.
W=-Pext × ∆V
= -(1.0) × (31.0) litre-atm
= - (31.0) × 101.3 J = - 3140.3 J
|
127 videos|245 docs|87 tests
|
FAQs on Thermodynamics: Common Terms, State Function, Reversible & Irreversible Processes - Chemistry Class 11 - NEET
| 1. What is thermodynamics and why is it important? |  |
| 2. What are the key differences between the system and the surroundings in thermodynamics? |  |
| 3. What are the basic thermodynamic terms that one should know? |  |
| 4. Can you explain the difference between reversible and irreversible processes in thermodynamics? |  |
| 5. What are the laws of thermodynamics and what do they state? |  |