Time and Work | Quantitative Techniques for CLAT PDF Download
| Table of contents |

|
| What is Time and Work? |

|
| Important Terms |

|
| Types of Questions from Time and Work |

|
| Concept of Efficiency |

|
| Solved Examples |

|
What is Time and Work?
Time and Work is the arithmetic concept that studies that studies the relationship between work, time, and efficiency. It is based on the principle of proportionality, where work is directly proportional to both time and efficiency, and efficiency is inversely proportional to time when the amount of work is constant.
Important Terms
The important terms related to time and work are given below:
- Rate of Work: The rate of work( R)is the fraction of work completed per unit time. If a person takes T days to complete a job, their rate is R=1/T (work per day).
- Time Taken: Rate of work and time are inversely proportional to each other. Thus, R = 1/T
- Work Done: It takes (T) time to complete a certain amount of work (W). The number of units of work done per unit time. Thus, Work Done (W) = Time (T) * Rate of Work (R)
- Negative Work: Assume that there are two people, A and B who have been assigned to build a table. Here, work refers to the building of a table. Also, assume that there is another person C who is assigned the task of damaging the table. Now, work done by C is termed as negative work as C is effectively lowering the amount of work done by A and B.
Types of Questions from Time and Work
There are some specific types of questions from Time and Work that usually come in exams. Some of the important types of questions from time and work are as follows:
- Time and Work Questions involving individual efficiencies
In such questions, the rates at which some individuals complete work alone are given and you are required to calculate the rate at which they can complete the work together and vice versa. - Time and Work Questions involving group efficiencies
These involve groups of people working together, often with equal efficiencies. The focus here is on calculating total work done when multiple people or identical workers are involved.
To solve problems on ‘time and work’, the following simple facts should be remembered:
- If a person can do work in 5 days, then in one day, he will do 1/5th of the whole work. Conversely, if a man can do 1/5th of the work in one day, he will complete the whole work in 5 days.
- If the number of men engaged to do a piece of work is increased in a certain ratio, the time required to do the same work will be decreased in the same ratio and vice versa. Thus, if the number of men is changed in the ratio of 3:7, the time required will be changed in the ratio of 7:3.

- If A is thrice as good as B, then
- In a given amount of time, A will be able to do 3 times the work B does. Ratio of work done by A and B (at the same time) = 3 : 1.
- For the same amount of work, B will take thrice the time as much as A takes. Ratio of time taken by A and B (same work done) = 1 : 3.
- To sum up, if M1 persons working T1 hours a day can do W1 work in D1 days and M2 persons working H2 hours a day can do W2 work in D2 days, then the following equation will hold good.
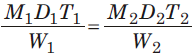
Example: A does work in 10 days and B does the same work in 15 days. How many days they will take to do the work together.
Solution: A does the work in 10 days, so A’s one-day work = 1/10
B does the work in 15 days, so B’s one day work = 1/15
Work done by A and B in one day = 1/10 + 1/15 = 5/30 = 1/6
Thus, A and B together will be able to finish the work in 6 days.
Example: A builder appoints three construction workers Akash, Sunil and Rakesh on one of his sites. They take 20, 30 and 60 days respectively to do a piece of work. How many days will it take Akash to complete the entire work if he is assisted by Sunil and Rakesh every third day?
Solution: Total work done by Akash, Sunil and Rakesh in 1 day = {(1/20) + (1/30) + (1/60)} = 1/10
Work done along by Akash in 2 days = (1/20) × 2 = 1/10
Work Done in 3 days (1 day of all three together + 2 days of Akash’s work) = (1/10) + (1/10) = 1/5
So, work done in 3 days = 1/5
Time taken to complete the work = 5×3 = 15 days
Example: To complete a piece of work, Samir takes 6 days and Tanvir takes 8 days alone respectively. Samir and Tanvir took Rs.2400 to do this work. When Amir joined them, the work was done in 3 days. What amount was paid to Amir?
Solution: Total work done by Samir and Tanvir = {(1/6) + (1/8)} = 7/24
Work done by Amir in 1 day = (1/3) – (7/24) = 1/24
Amount distributed between each of them = (1/6) : (1/8) : (1/24) = 4:3:1
Amount paid to Amir = (1/24) × 3 × 2400 = Rs.300
Concept of Efficiency
Efficiency denotes the amount of work done by any person in 1 day. We use this concept to compare the quality of a worker, i.e., if a worker is more efficient than any other worker, then we can say he/she can do more work in 1 day as compared to other workers.
- The ratio of the efficiencies of two workers is proportional to the time taken by them to complete a work.
- If a worker is less efficient than he/she will take more time to complete the work.
- If a worker is more efficient than he/she will take less time to complete the work.
Example: A is 3 times as efficient as B. If B alone can complete the work in 12 days, then A alone can complete the work in how many days?
Solution: According to the question, the ratio of the efficiency of A and B is 3 : 1
We know that the ratio of the efficiency is inversely proportional to the ratio of the time taken
So, the ratio of the time taken by A and B to complete the work will be 1 : 3
Let us assume A alone completes the work in x days and B alone completes the work in 3x days
3x=12
x=4
Therefore, A alone can complete the work in 4 days.
Note: The concept of efficiency is widely used to equate the works of men, women, and children.
Example: Dev completed the school project in 20 days. How many days will Arun take to complete the same work if he is 25% more efficient than Dev?
Solution: Let the days taken by Arun to complete the work be x
The ratio of time taken by Arun and Dev = 125:100 = 5:4
5:4 :: 20:x
⇒ x = {(4×20) / 5}
⇒ x = 16
Solved Examples
Example 1. A tyre has two punctures. The first puncture alone can empty the tyre in 9 minutes and 2nd puncture alone can empty the tyre in 6 minutes. How long will both the punctures take to flat the tyre.
Sol. The first puncture takes 9 minutes to flatten the tyre, so first puncture’s one-minute work = 1/ 9 The second puncture takes 6 minutes to flatten that tyre, so second puncture’s one-minute work = 1/6
So work done by both punctures in one minute = 1/9 + 1/6 = 5/18
Thus, both punctures together will take 18/5 minutes to flatten the tyre.
Example 2. A and B together can finish a job in 15 days. If A alone can finish the job in 25 days, in how many days can B alone finish the job.
Sol. A and B together can finish the job in 15 days, so their one day work = 1/15
A alone can finish the job in 25 days, so A’s one day work = 1/25B’s one day work =
Thus, B alone can finish the job in 75/2 days.
Example 3. A and B together can build a house in 25 days. They work together for 15 days and then B goes away. A finishes the rest of the work in 20 days. How long will take each to finish the job working separately?
Sol. A+B can finish the work in 25 days, so one day work = 1/25
They work together for 15 days, so the work done by A+B in 15 days =Remaining job =

To complete 2/5 of work in 20 days, A can complete one work in
= 50 days
B’s rate= 1/25 – 1/50 = 1/50
So B can finish the whole work in 50 days.
A man can do a job in 5 days but with the help of his son he can do it is 3 days. In what time can the son do it alone.
Example 4. A can finish a job in 10 days, B in 12 days and C in 10 days. In how many days will they finish the job if they work together.
Sol. A’s one day work = 1/10
B’s one day work = 1/12
C’s one day work = 1/10
A+B+C’s one day work = 1/10 + 1/12 + 1/10 = (6+5+6)/60 = 17/60
Thus, together they can complete the work in 60/17 days.
Example 5. M and N together can complete a task in 20 days. If M alone can complete the task in 30 days, in how many days can N alone complete the task?
Sol. M and N together complete the task in 20 days, so their combined one-day work = 1/20
M alone completes the task in 30 days, so M’s one-day work = 1/30
N’s one-day work= 1/20-1/30=1/60
Thus, N alone can complete the task in 1/1/60= 60 days
|
49 videos|179 docs|73 tests
|
FAQs on Time and Work - Quantitative Techniques for CLAT
| 1. What is the basic concept of Time and Work in mathematics? |  |
| 2. What are the different types of questions that can be asked in Time and Work problems? |  |
| 3. How is efficiency defined in the context of Time and Work? |  |
| 4. What are some tips and tricks to solve Time and Work problems quickly? |  |
| 5. Can you provide an example of a Time and Work problem and its solution? |  |





















