Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Trigonometric Graphs
Trigonometric Graphs | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Drawing Trig Graphs
Why do we need to know what trig graphs look like?
- Trigonometric graphs, commonly referred to as trig graphs, find applications across various mathematical domains.
- For instance, their oscillatory behavior proves instrumental in modeling phenomena such as pendulum swings or tide heights.
How do we draw trig graphs?
- Being acquainted with the general style of trigonometric graphs facilitates quick sketching and aids in finding values or angles without reliance solely on calculators.
- All trigonometric graphs conform to a specific pattern - they initiate from a "starting point" and then exhibit a regular occurrence every 90 degrees.
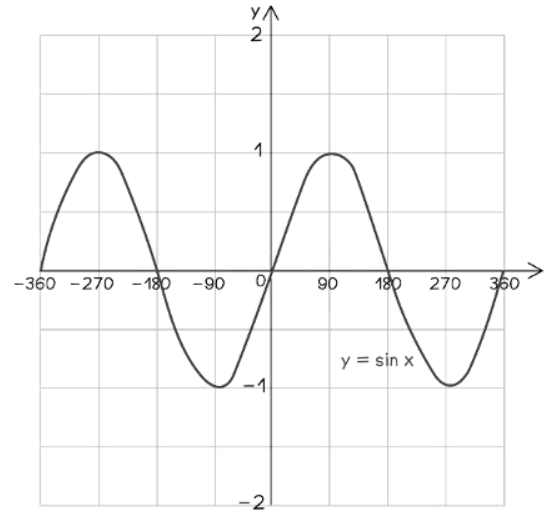
Sine Graph:
- y = sin x
- Starts at (0,0)
- Every 90° it cycles through 1, 0, -1, 0, ...
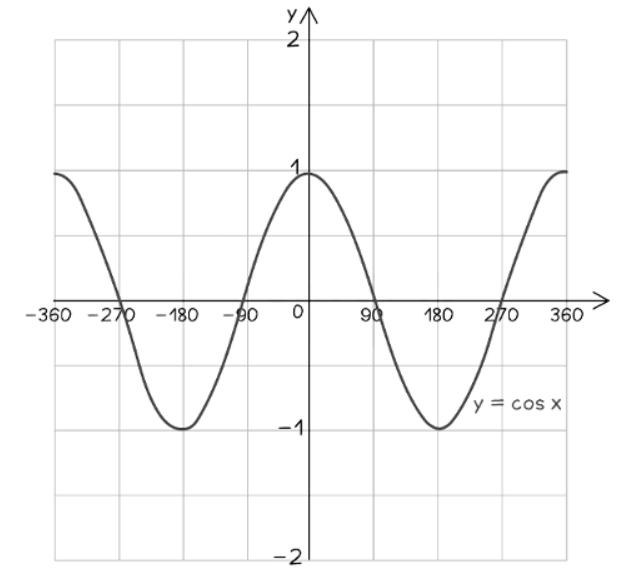
Cosine Graph:
- y = cos x
- Starts at (0, 1)
- Every 90° it cycles through 0, -1, 0, 1, ...
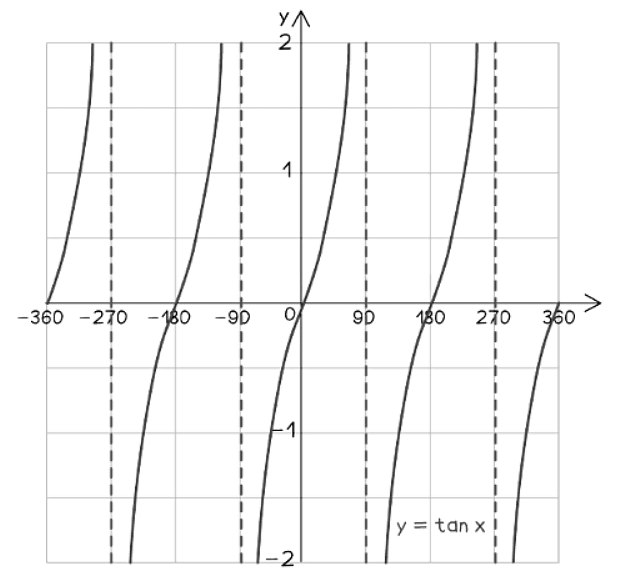
Tangent Graph:
- y = tan x
- Starts at (0, 0)
- Every 90° it is either 0 or an asymptote
- An asymptote is a line that a graph gets ever closer to, without ever crossing or touching it
The document Trigonometric Graphs | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on Trigonometric Graphs - Mathematics for GCSE/IGCSE - Class 10
| 1. Can you explain how to draw trigonometric graphs step by step? |  |
Ans. To draw trigonometric graphs, start by plotting the key points for one period of the function, such as the maximum and minimum points, the x-intercepts, and the points at which the function starts repeating itself. Then, connect these points smoothly to form the graph. Make sure to label the axes and key points on the graph for clarity.
| 2. What are the important characteristics of a trigonometric graph? | |
Ans. Some important characteristics of a trigonometric graph include amplitude, period, phase shift, and vertical shift. The amplitude determines the height of the graph, the period is the length of one complete cycle, the phase shift is any horizontal translation of the graph, and the vertical shift moves the entire graph up or down.
| 3. How do you identify the period of a trigonometric function from its equation? | |
Ans. To identify the period of a trigonometric function from its equation, look for the coefficient of x inside the function. The period is calculated as 2π divided by this coefficient. For example, if the function is y = sin(2x), the period would be 2π/2 = π.
| 4. What is the significance of the amplitude in a trigonometric graph? | |
Ans. The amplitude in a trigonometric graph determines the maximum distance the graph extends from the midline. It is half the distance between the maximum and minimum values of the function and affects the height of the graph. A larger amplitude results in a taller graph, while a smaller amplitude results in a shorter graph.
| 5. How can you use trigonometric graphs to solve real-life problems? | |
Ans. Trigonometric graphs can be used to model and solve various real-life problems involving periodic phenomena, such as sound waves, ocean tides, and electrical currents. By analyzing the amplitude, period, and phase shift of the graph, one can make predictions and solve practical problems related to these phenomena.
About this Document
Oct 23, 2025
Last updated
Related Exams
Document Description: Trigonometric Graphs for Class 10 2025 is part of Mathematics for GCSE/IGCSE preparation.
The notes and questions for Trigonometric Graphs have been prepared according to the Class 10 exam syllabus. Information about Trigonometric Graphs covers topics
like Drawing Trig Graphs and Trigonometric Graphs Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Trigonometric Graphs.
Introduction of Trigonometric Graphs in English is available as part of our Mathematics for GCSE/IGCSE
for Class 10 & Trigonometric Graphs in Hindi for Mathematics for GCSE/IGCSE course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Trigonometric Graphs | Mathematics for GCSE/IGCSE - Class 10
Description
Full syllabus notes, lecture & questions for Trigonometric Graphs | Mathematics for GCSE/IGCSE - Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics for GCSE/IGCSE | Best notes, free PDF download
Information about Trigonometric Graphs
In this doc you can find the meaning of Trigonometric Graphs defined & explained in the simplest way possible. Besides explaining types of
Trigonometric Graphs theory, EduRev gives you an ample number of questions to practice Trigonometric Graphs tests, examples and also practice Class 10
tests
Related Searches
Trigonometric Graphs | Mathematics for GCSE/IGCSE - Class 10
,Trigonometric Graphs | Mathematics for GCSE/IGCSE - Class 10
,Extra Questions
,Sample Paper
,Viva Questions
,video lectures
,Semester Notes
,Trigonometric Graphs | Mathematics for GCSE/IGCSE - Class 10
,Objective type Questions
,practice quizzes
,Free
,mock tests for examination
,ppt
,Important questions
,MCQs
,Previous Year Questions with Solutions
,past year papers
,Summary
,study material
,shortcuts and tricks
,Exam
;
Additional Information about Trigonometric Graphs for Class 10 Preparation
Trigonometric Graphs Free PDF Download
The Trigonometric Graphs is an invaluable resource that delves deep into the core of the Class 10 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Trigonometric Graphs now and kickstart your journey towards success in the Class 10 exam.
Importance of Trigonometric Graphs
The importance of Trigonometric Graphs cannot be overstated, especially for Class 10 aspirants.
This document holds the key to success in the Class 10 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Trigonometric Graphs Notes
Trigonometric Graphs Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Trigonometric Graphs.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Trigonometric Graphs Notes on EduRev are your ultimate resource for success.
Trigonometric Graphs Class 10 Questions
The "Trigonometric Graphs Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Trigonometric Graphs on the App
Students of Class 10 can study Trigonometric Graphs alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Trigonometric Graphs,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Trigonometric Graphs is prepared as per the latest Class 10 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily