Type of Earthquake Waves | Geography for UPSC CSE PDF Download
Seismic waves and earth’s interior: P waves, S waves, L waves
Now, first of all, You should understand Why does the earth shake?
- The release of energy occurs along a fault.
- A fault is a sharp break in the crustal rock layer.
- Rocks along a fault tend to move in opposite directions. But the friction exerted by the overlying rock strata prevents the rock layer's movement, with time pressure builds up.
- Under intense pressure, the rock layer, at a certain point, overcomes the friction offered by the overlying layer and undergoes an abrupt movement generating shockwaves.
- This causes a release of energy, and the energy waves travel in all directions.
- The point where the energy is released is called the s focus of an earthquake. Alternatively, it is called the hypocentre.
- The energy waves travelling in different directions reach the surface. The point on the surface, nearest to the focus, is called the epicentre. It is the first one to experience the waves. It is a point directly above the focus. Question for Type of Earthquake WavesTry yourself:Which wave is also known as a longitudinal wave?View Solution
Earthquake Waves
Now you have to guess which waves are more suitable to study the interior of the earth.
- Body waves
- Surface waves
- All-natural earthquakes occur in the lithosphere (depth up to 200 km from the surface of the earth).
- An instrument called ‘seismograph’ records the waves reaching the surface.
- Earthquake waves are basically of two types – body waves and surface waves.
- Body waves are generated due to the release of energy at the focus and move in all directions travelling through the earth's body.
- Hence, the name body waves.
- The body waves interact with the surface rocks and generate a new set of waves called surface waves. These waves move along the surface.
- The velocity of waves changes as they travel through materials with different elasticity (stiffness) (Generally density with few exceptions). The more elastic the material is, the higher is the velocity.
- Their direction also changes as they reflect or refract when coming across materials with different densities.
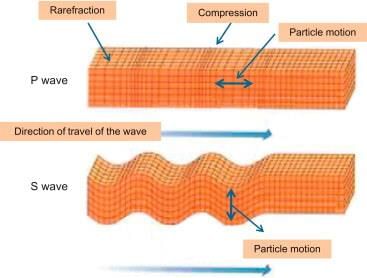
- There are two types of body waves. They are called P and S-waves.
The behaviour of Earthquake Waves
The earthquake waves are measured with the help of a seismograph and are of three types—
- The ‘P’ waves or primary waves (longitudinal nature)
- Secondary waves or ‘S’ waves (transverse in nature)
- Surface waves or ‘L’ waves are long.
The velocity and direction of the earthquake waves change when the medium through which they are travelling changes.
When an earthquake or underground nuclear test sends shock waves through the Earth, the cooler areas generally are rigid and transmit these waves at a higher velocity than the hotter regions.
Primary Waves (P waves)
- Also called the longitudinal or compressional waves.
- Particles of the medium vibrate along the direction of propagation of the wave.
- P-waves move faster and are the first to arrive at the surface.
- These waves are of high frequency.
- They can travel in all mediums.
- The velocity of P waves in Solids > Liquids > Gases
- Their velocity depends on y shear strength or elasticity of the material.
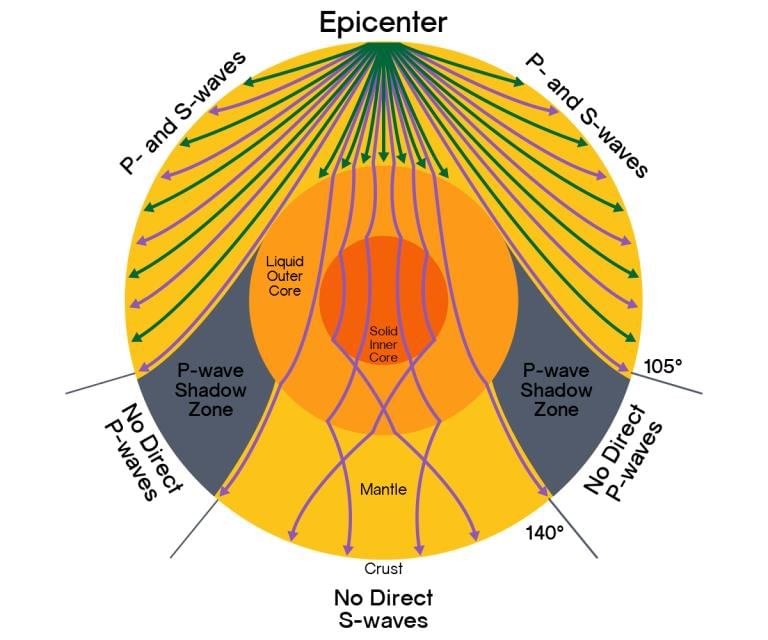
- The shadow zone for ‘P’ waves is an area that corresponds to an angle between 103° and 142°.
- This gives clues about the Solid inner core.
Secondary Waves (S waves)
- Also called as transverse or distortion waves.
- Analogous to water ripples or light waves.
- S-waves arrive at the surface with some time lag.
- A secondary wave cannot pass through liquids or gases.
- These waves are of high-frequency waves.
- Travel at varying velocities (proportional to shear strength) through the solid part of the Earth’s crust, mantle.
- The shadow zone of ‘S’ waves extends y almost halfway around the globe from the earthquake’s focus.
- The shadow zone for ‘S’ waves is an area that corresponds to an angle between 103° and 103°.
- This observation led to the discovery of the liquid outer core. Since S waves cannot travel through liquid, they do not pass through the liquid outer core.
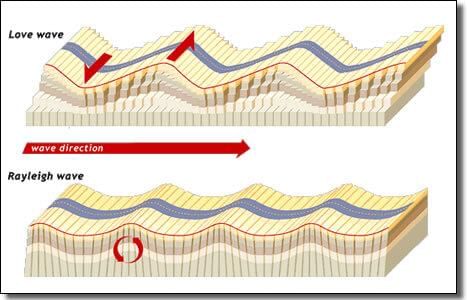
Surface Waves (L waves)
- Also known as long-period waves.
- They are low frequency, long wavelength, and transverse vibration.
- Generally, they affect the surface of the Earth only and die out at a smaller depth.
- Develop in the immediate neighbourhood of the epicentre.
- They cause displacement of rocks, and hence, the collapse of structures occurs.
- These waves are responsible for most of the destructive force of the earthquake.
- They are recorded last on the seismograph.
Propagation of Earthquake Waves
- Different types of earthquake waves travel in various manners. As they move or propagate, they cause vibration in the rocks' body through which they pass.
- P-waves vibrate parallel to the direction of the wave. This exerts pressure on the material in the direction of the propagation.
- As a result, it creates density differences in the material leading to stretching and squeezing the material.
- The other two waves vibrate perpendicular to the direction of propagation.
- The direction of vibrations of S-waves is perpendicular to the wave direction in the vertical plane. Hence, they create s troughs and crests in the material through which they pass. Question for Type of Earthquake WavesTry yourself:Which wave has the shadow zone between 103 and 140 degrees from the given earthquake?View Solution
The emergence of Shadow Zone
- Earthquake waves get recorded in seismographs located at far off locations.
- However, there exist some specific areas where the waves are not reported. Such a zone is called the ‘shadow zone’.
- The study of different events reveals that for each earthquake, there exists an altogether different shadow zone.
- It was observed that seismographs located at any distance within 105 ° from the epicentre, recorded the arrival of both P and S-waves.
- However, the seismographs located beyond 145 ° from the epicentre, record the arrival of P-waves, but not that of S- waves.
- Thus, a zone between ° 105 ° and 145 ° from the epicentre was identified as the shadow zone for h both the types of waves. The entire zone beyond 105 ° does not receive S-waves.
- The shadow zone of S-wave is much larger than that of the P-waves. P-waves' shadow zone appears as a band around the earth between 105 ° and 145 ° away from the epicentre.
- The shadow zone of S-waves is not only larger in extent, but it is also a little over 40 per cent of the earth’s surface.
How can these properties of ‘P’ and ‘S’ waves help determine the earth’s interior?
Reflection causes waves to rebound, whereas refraction makes waves move in different directions.
The variations in the direction of waves are inferred with the help of their record on the seismograph.
Change in densities greatly varies the wave velocity.
By observing the changes in velocity, the density of the earth as a whole can be estimated.
By observing the changes in the direction of the waves (emergence of shadow zones), different layers can be identified.
Why can S-waves not travel through liquids?
S-waves are shear waves, which move particles perpendicularly to their direction of propagation.
They can propagate through solid rocks because these rocks have enough shear strength.
The shear strength is one of the forces that hold the rock together, and prevent it from falling into pieces.
Liquids do not have the same shear strength: that is why, if you take a glass of water and suddenly remove the glass, the water will not keep its glass shape and will flow away.
It is just a matter of rigidity: S-waves need a medium rigid enough to propagate. Hence, S-waves do not propagate through liquids.
|
175 videos|477 docs|193 tests
|
FAQs on Type of Earthquake Waves - Geography for UPSC CSE
| 1. What are seismic waves and how do they help determine the earth's interior? |  |
| 2. What are P-waves and S-waves and how do they differ in their propagation? |  |
| 3. What is the significance of the emergence of the shadow zone in determining the Earth's interior? |  |
| 4. Why can S-waves not travel through liquids? |  |
| 5. How do seismic waves help in predicting and studying earthquakes? |  |

|
Explore Courses for UPSC exam
|

|


















