Simple Harmonic Motion | Physics Class 11 - NEET PDF Download
Simple Harmonic Motion
The oscillation which can be expressed in terms of single harmonic function, i.e., sine or cosine function, is called harmonic oscillation.
A harmonic oscillation of constant amplitude and of single frequency under a restoring force whose magnitude is proportional to the displacement and always acts towards mean position is called Simple Harmonic Motion (SHM).
 Simple Harmonic Motion
Simple Harmonic Motion
A simple harmonic oscillation can be expressed as
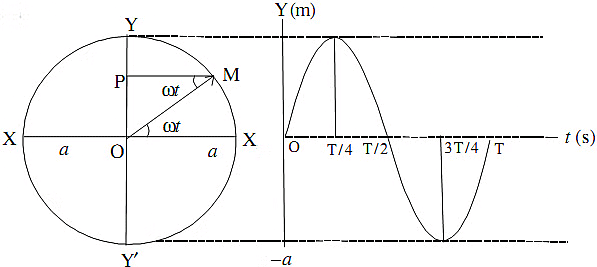
y = a sin ωt or y = a cos ωt
Where a = amplitude of oscillation.
Non-harmonic Oscillation
A non-harmonic oscillation is a combination of two or more than two harmonic oscillations.
It can be expressed as y = a sin ωt + b sin 2ωt
Some Terms Related to SHM
(i) Time Period: Time taken by the body to complete one oscillation is known as time period. It is denoted by T.
(ii) Frequency: The number of oscillations completed by the body in one second is called frequency. It is denoted by v.
Its SI unit is ‘hertz’ or ‘second-1.
Frequency = 1 / Time period
(iii) Angular Frequency: The product of frequency with factor 2π is called angular frequency. It is denoted by ω.
Angular frequency (ω) = 2πv
Its SI unit is ‘hertz’ or ‘second-1.
(iv) Displacement: A physical quantity which changes uniformly with time in a periodic motion is called displacement. It is denoted by y.
(v) Amplitude: The maximum displacement in any direction from mean position is called amplitude. It is denoted by a.
(vi) Phase: A physical quantity which express the position and direction of motion of an oscillating particle, is called phase. It is denoted by φ.
Simple harmonic motion is defined as the projection of a uniform circular motion on any diameter of a circle of reference.
Some Important Formulae of SHM
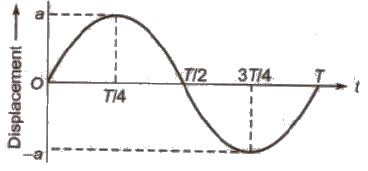
(i) Displacement in SHM at any instant is given by
y = a sin ωt
or y = a cos ωt
where a = amplitude and
ω = angular frequency.
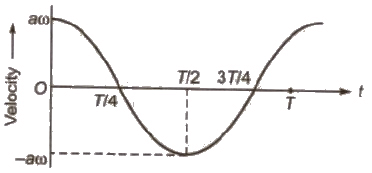
(ii) Velocity of a particle executing SHM at any instant is given by
v = ω √(a2 – y2)
At mean position y = 0 and v is maximum
vmax = aω
At extreme position y = a and v is zero.
(iii) Acceleration of a particle executing SHM at any instant is given by
A or α = – ω2 y
Negative sign indicates that the direction of acceleration is opposite to the direction in which displacement increases, i.e., towards mean position.
At mean position y = 0 and acceleration is also zero.
At extreme position y = a and acceleration is maximum
Amax = – aω2
(iv) Time period in SHM is given by
T = 2π √Displacement / Acceleration
Graphical Representation:
(i) Displacement – Time Graph:
(ii) Velocity – Time Graph:
(iii) Acceleration – Time Graph:
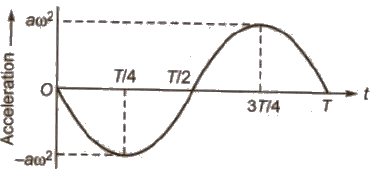
Note: The acceleration is maximum at a place where the velocity is minimum and vice – versa.
For a particle executing SHM, the phase difference between
(i) Instantaneous displacement and instantaneous velocity
= (π / 2) rad
(ii) Instantaneous velocity and instantaneous acceleration
= (π / 2) rad
(iii) Instantaneous acceleration and instantaneous displacement
= π rad
The graph between velocity and displacement for a particle executing SHM is elliptical.
Force in SHM
We know that, the acceleration of body in SHM is α = -ω2 x
Applying the equation of motion F = ma,
We have, F = – mω2 x = -kx
Where, ω = √k / m and k = mω2 is a constant and sometimes it is called the elastic constant.
In SHM, the force is proportional and opposite to the displacement.
Energy in SHM
The kinetic energy of the particle is K = 1 / 2 mω2 (A2 – x2)
From this expression we can see that, the kinetic energy is maximum at the centre (x = 0) and zero at the extremes of oscillation (x ± A).
The potential energy of the particle is U = 1 / 2 mω2 x2
From this expression we can see that, the potential energy has a minimum value at the centre (x = 0) and increases as the particle approaches either extreme of the oscillation (x ± A).
Total energy can be obtained by adding potential and kinetic energies. Therefore,
E = K + U
= 1 / 2 mω2 (A2 – x2) + 1 / 2 mω2 x2
= 1 / 2 mω2 A2
where A = amplitude
m = mass of particle executing SHM.
ω = angular frequency and
v = frequency
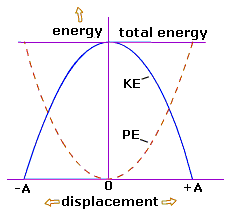 Changes of Kinetic and Potential Energies during Oscillations
Changes of Kinetic and Potential Energies during Oscillations
When a particle of mass m executes SHM with a constant angular frequency (I), then time period of oscillation
T = 2π √Inertia factor / Spring factor
In general, inertia factor = m, (mass of the particle)
Spring factor = k (force constant)
How the different physical quantities (e.g., displacement, velocity, acceleration, kinetic energy etc) vary with time or displacement are listed ahead in tabular form:
S.No. Name of the equation Expression of the equation Remarks 1.
Displacement-time
x varies between + A and - A
2.
Velocity-time
v varies between + Aω and - A ω
3.
Acceleration-time
a varies between + Aω2 and - Aω2
4.
Kinetic energy-time
K varies between and
5.
Potential energy-time
U varies between and
6.
Total energy-time
(E = K + U)
E is constant
7.
Velocity-displacement
v = 0 at x = ±4 and at x = 0 , v = ± Aω
8.
Acceleration-displacement
a = - ω2X
9.
Kinetic energy-displacement
10.
Potential energy-d displacement
11.
Total energy-d displacement
x = ± A
E is constant
Oscillations of Liquid in a U – tube
If a liquid is filled up to height h in both limbs of a U-tube and now liquid is depressed upto a small distance y in one limb and then released, then liquid column in U-tube start executing SHM.
The time period of oscillation is given by
T = 2π √h / g
Oscillations of a floating cylinder in liquid is given by
T = 2π √l / g
where I = length of the cylinder submerged in liquid in equilibrium.
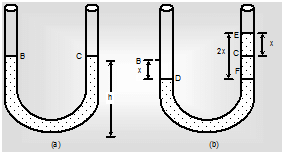 Oscillations of Liquid In U-Tube
Oscillations of Liquid In U-Tube
Vibrations of a Loaded Spring
When a spring is compressed or stretched through a small distance y from mean position, a restoring force acts on it.
Restoring force (F) = – ky
where k = force constant of spring.
If a mass m is suspended from a spring then in equilibrium,
mg = kl
This is also called Hooke’s law.
Time period of a loaded spring is given by:
T = 2π √m / k
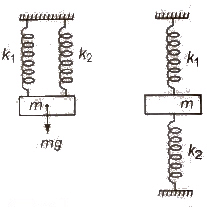
When two springs of force constants k1 and k2 are connected in parallel to mass m as shown in figure, then
(i) Effective force constant of the spring combination
k = k1 + k2
(ii) Time period T = 2π √m / (k1 + k2)
When two springs of force constant k1 and k2 are connected in series to mass m as shown in figure, then
(i) Effective force constant of the spring combination
1 / k = 1 / k1 + 1 / k2
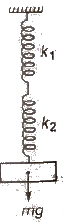
(ii) Time period T = 2π √m(k1 + k2) / k1k2
|
95 videos|367 docs|98 tests
|
FAQs on Simple Harmonic Motion - Physics Class 11 - NEET
| 1. What is Simple Harmonic Motion (SHM) and what are its characteristics? |  |
| 2. What are some important formulae related to SHM? |  |
| 3. How is the force in SHM derived and what is its significance? |  |
| 4. How does energy transform in SHM? |  |
| 5. What is the oscillation of liquid in a U-tube and how does it relate to SHM? |  |

















