Understanding Elementary Shapes Summary Class 6 Maths Chapter 5
In our surroundings, numerous forms composed of lines and curves can be observed, such as line segments, angles, triangles, polygons, and circles, among others. These shapes vary in both size and dimensions.
Measuring Line Segments
A line segment is a fixed part of the line, so it must have some length. We can compare any line segment on the basis of their length. The length of a line segment is the distance between its endpoints.
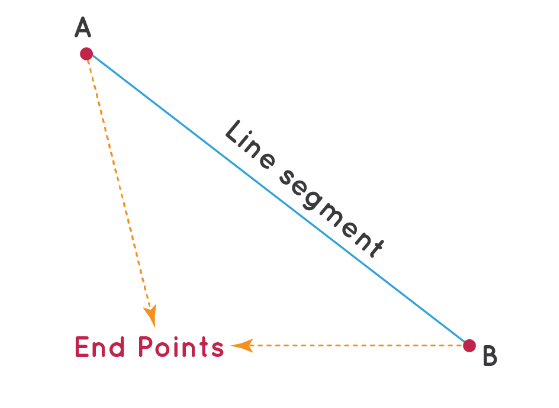 Line Segment
Line Segment
In this section, the focus is on understanding and measuring line segments.
Comparison by Observation:
- We can tell which line segment is greater than other just by observing the two line segments but it is not sure.
- Here we can clearly say that AB > CD but sometimes it is difficult to tell which one is greater.
 Comparison by Observation
Comparison by Observation
Comparison by Tracing:
- Tracing paper is used to compare line segments.
- By tracing one segment and overlaying it on another, a visual determination of length can be made.
- Limitations include the need for precision in tracing and the impracticality of tracing every time a comparison is required.
Comparison using Ruler and a Divider
- We can use a ruler to measure the length of a line segment.
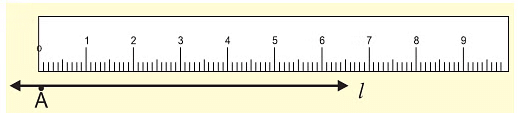 Ruler
Ruler - Put the zero mark at point A and then move toward l to measure the length of the line segment, but it may have some errors on the basis of the thickness of the ruler.
This could be made accurate by using a Divider.
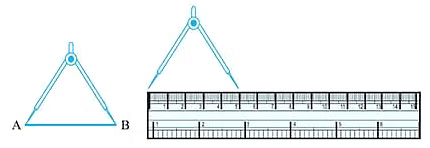 Using a divider
Using a divider- Put the one end of the divider on point A and open it to put another end on point B.
- Now pick up the divider without disturbing the opening and place it on the ruler so that one end lies on “0”.
- Read the marking on the other end and we can compare the two line.
Angles – ‘Right’ and ‘Straight’
Right angle: The measure of a right angle is 90° and hence that of a straight angle is 180°.
Straight angle: An angle whose measure is 180°.
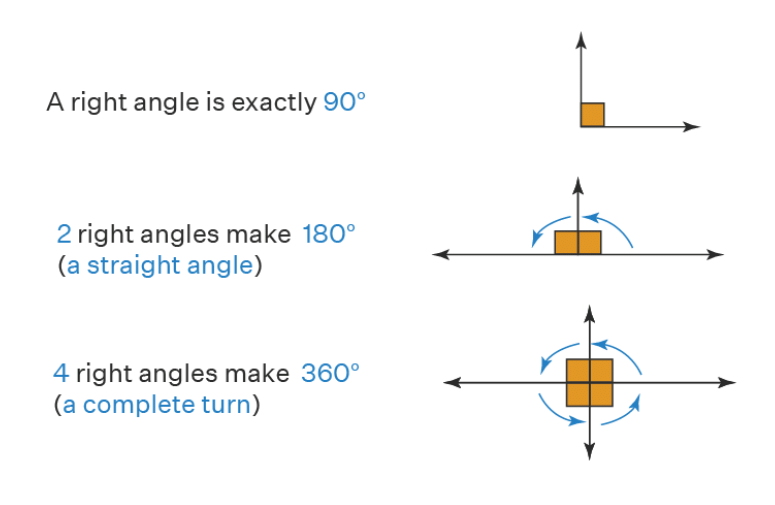 Right and Straight Angles
Right and Straight Angles
- When we move from North to East then it forms an angle of 90° which is called Right Angle. revolution is a right angle,
When we move from North to South then it forms an angle of 180° which is called Straight Angle. revolution is a straight angle.
 Directions
Directions
When we move four right angles in the same direction then we reach to the same position again i.e. if we make a clockwise turn from North to reach to North again then it forms an angle of 360° which is called a Complete Angle. This is called one revolution.
- An example of an angle is when the hand of a clock shifts from one location to another. This Clock below revolution or two right angles
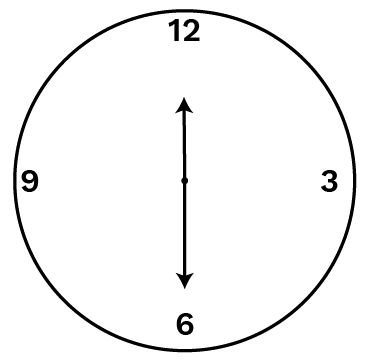 2 right angles
2 right angles - Clock below represents 1/4 of revolution or 1 right angles
 1 right angle
1 right angle - Clock below represents 3/4 of revolution or right angles.
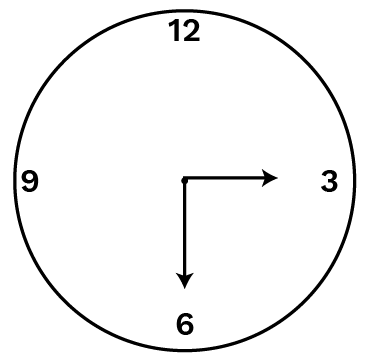 3 right angles
3 right angles - A right angle is 1/4 a revolution and a straight angle is 1/2 a revolution.
Angles – ‘Acute’, ‘Obtuse’ and ‘Reflex’
- Acute angle: An angle whose measure is more than 0° but less than 90°. Sea-saw, rooftop, opening book, etc. are examples of an acute angle.
- Obtuse angle: An angle whose measure is more than 90° but less than 180°. House, desk for book reading, etc. are examples of an obtuse angle.
- Reflex angle: An angle whose measure is more than 180° but less than 360° is called a reflex angle. A reflex angle is larger than a straight angle.
- Complete angle: An angle whose measure is 360°, is called a complete angle.
 Types of Angles
Types of Angles
Measuring Angles
To understand angles better, we don't just look at them, we measure them! We use a special unit called "degrees" to measure angles.
- One complete revolution is divided into 360 equal parts so each part is one degree. We write it as 360° and read as “three hundred sixty degrees".
- We can measure the angle using a ready to use device called Protractor.
- It has a curved edge which is divided into 180 equal parts. It starts from 0° to 180° from right to left and vice versa.
 ProtactorTo measure an angle using protractor-
ProtactorTo measure an angle using protractor-
- Place the protractor on the angle in such a way that the midpoint of protractor comes on the vertex B of the angle.
- Adjust it so that line BC comes on the straight line of the protractor.
- Read the scale which starts from 0° coinciding with the line BC.
- The point where the line AB comes on the protractor is the degree measure of the angle.
Hence, ∠ABC = 72°
Perpendicular Lines
When two lines intersect and the angle between them is a right angle, then the lines are said to be perpendicular. If a line AB is perpendicular to CD, we write AB ⊥ CD.
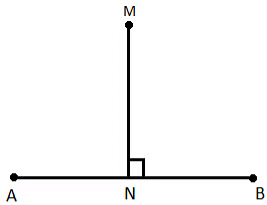 Perpendicular Lines
Perpendicular Lines
- In above, AB and MN are intersecting at point N and form a right angle. We will write it as
AB ⊥ MN or MN ⊥ AB.
Reads as AB is perpendicular to MN or MN is perpendicular to AB.
Perpendicular Bisector: If a perpendicular divides another line into two equal parts then it is said to be a perpendicular bisector of that line.
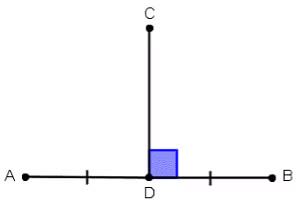 Here, CD is the perpendicular bisector of AB as it divides AB into two equal parts i.e. AD = DB.
Here, CD is the perpendicular bisector of AB as it divides AB into two equal parts i.e. AD = DB.
Classification of Triangles
Triangle is a polygon with three sides. It is the polygon with the least number of sides. Every triangle is of different size and shape. We classify them on the basis of their sides and angles.
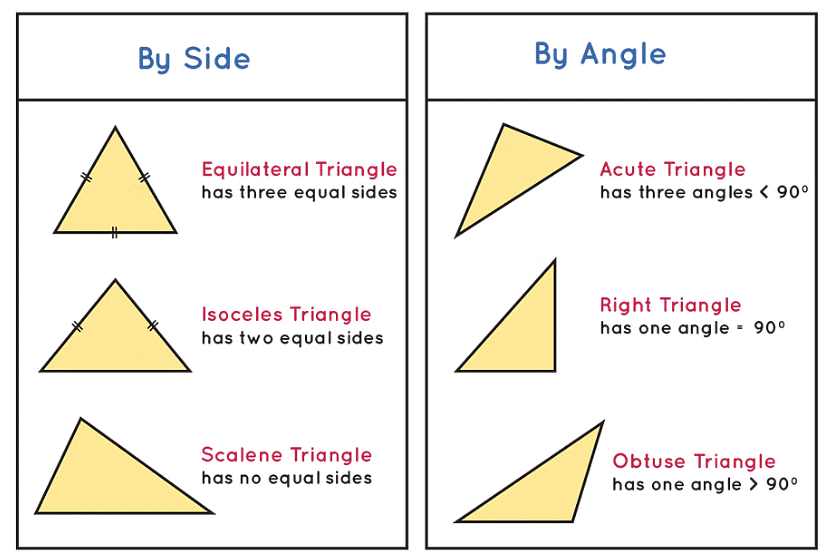
Types of Triangles based on Sides
(i) Equilateral triangle: A triangle having all sides equal, is called an equilateral triangle.
(ii) Isosceles triangle: A triangle having two sides equal, is called an isosceles triangle.
(iii) Scalene triangle: A triangle having all sides of different lengths is called a scalene triangle.
Types of Triangles based on Angles
(i) Acute triangle: A triangle each of whose angle measures less than 90° is called an acute triangle.
(ii) Right angled triangle: A triangle one of whose angle measures 90° is called a right angled triangle.
(iii) Obtuse triangle: A triangle one of whose angle measures more than 90° is called an obtuse triangle.
Quadrilateral
A plane figure bounded by four line segments is called a quadrilateral.
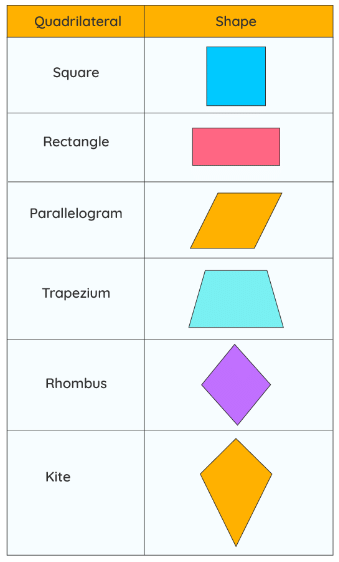 Types of Quadrilaterals
Types of Quadrilaterals
- A quadrilateral having opposite pair of sides parallel is called a parallelogram.
- A quadrilateral having only one pair of parallel sides is called a trapezium.
- A quadrilateral having opposite sides equal and each angle of 90° is called rectangle.
- If a quadrilateral is having all sides equal and each angle of 90°, it is called a square.
- A parallelogram having all of its sides equal is called a rhombus.
Polygons
Polygon is a closed figure bounded by three or more than three line segments.
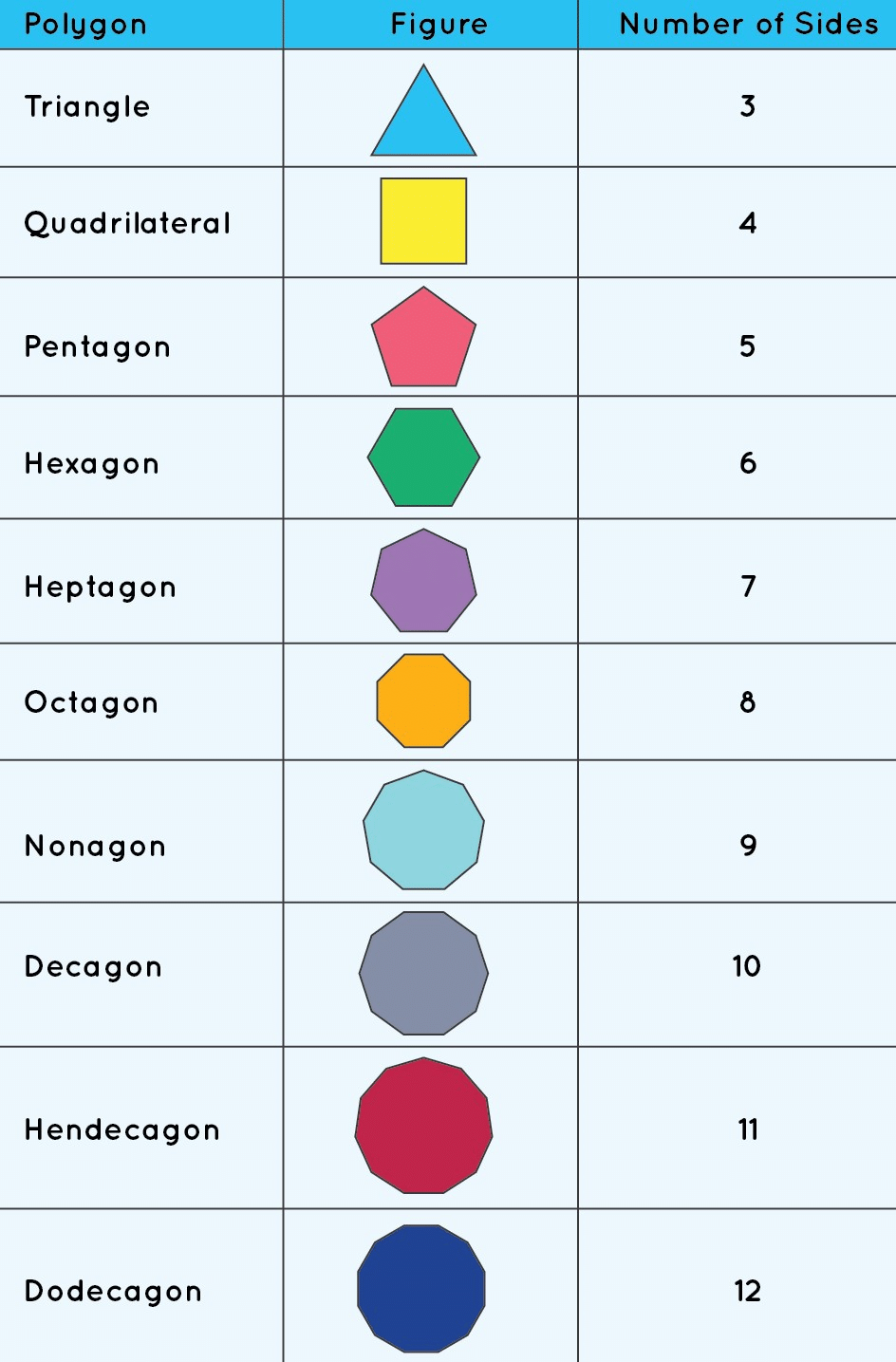 Types of Polygons
Types of Polygons
- If a polygon is bounded by 3 sides, it is called a triangle.
- If a polygon is bounded by 4 sides, it is called a quadrilateral.
- If a polygon is bounded by 5 sides, it is called a pentagon.
- If a polygon is bounded by 6 sides, it is called a hexagon.
Three dimensional shapes
The solid shapes having three dimensions are called 3D shapes.
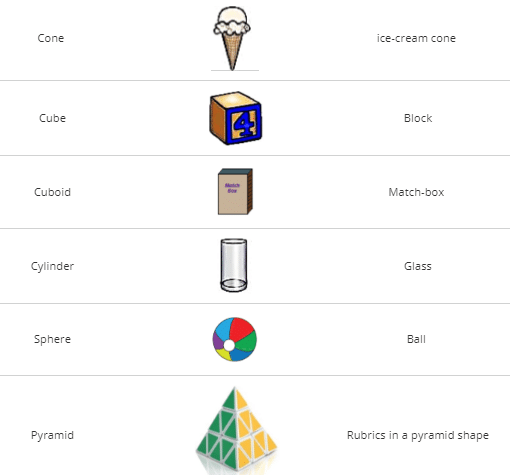 3D shapes around us
3D shapes around us
- Sphere: An object which is in the shape of a ball. It has a curved surface but no vertex and no edge.
- Cone: Objects in the form of ice-cream cone, a conical tent, birthday cap etc.
- Cylinder: A circular pipe, a circular pillar etc. are in the shape of cylinder. It has one curved surface and two circular faces at its ends.
- Cuboid: A brick, a matchbox, a book, etc. are in the shape of a cuboid. It has length, breadth and height. It has 6 rectangular faces. Two faces meet at a line segment called an edge. Three edges meet at a point called vertex.
- Cube: A cuboid whose length breadth and height are equal e.g., dice, ice cubes etc. A cube has 6 square faces, 12 edges and 8 vertices.
- Pyramid: A solid whose base in a plane rectilinear figure and whose side faces are triangles having a common vertex.
|
82 videos|273 docs|69 tests
|
FAQs on Understanding Elementary Shapes Summary Class 6 Maths Chapter 5
| 1. How can elementary shapes be classified? |  |
| 2. What is the difference between a 2D shape and a 3D shape? |  |
| 3. How can we identify different shapes in our surroundings? |  |
| 4. Why is it important to understand elementary shapes? |  |
| 5. How can we use elementary shapes to create composite shapes? |  |

















