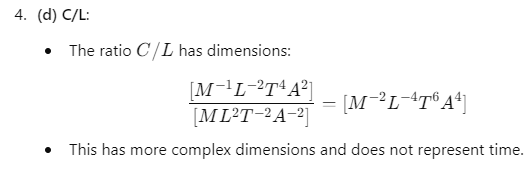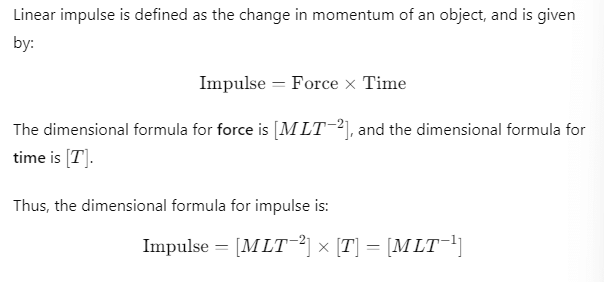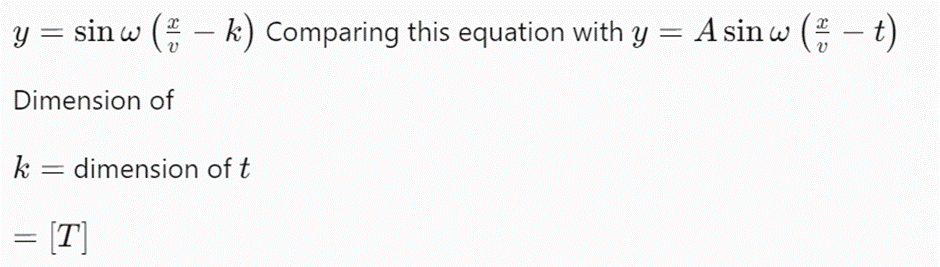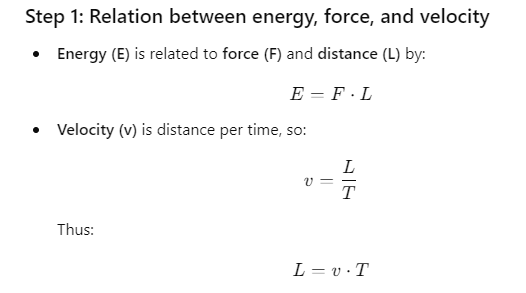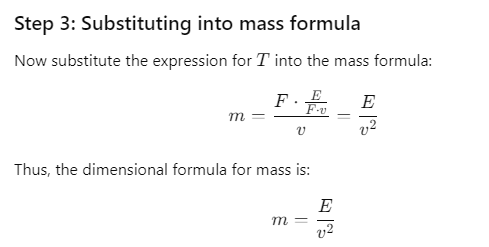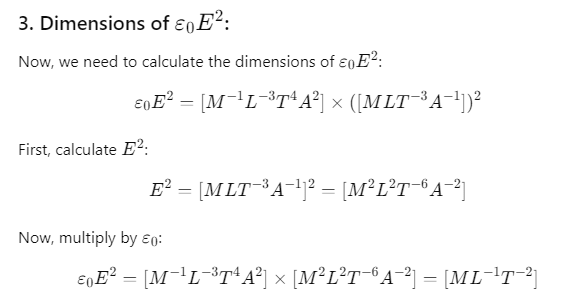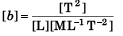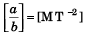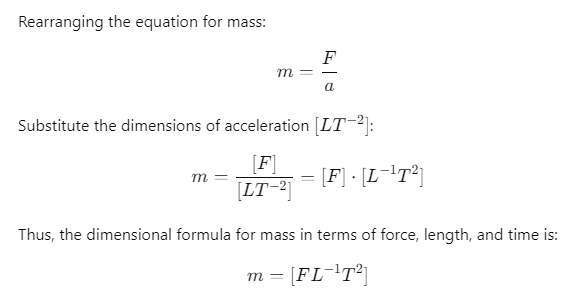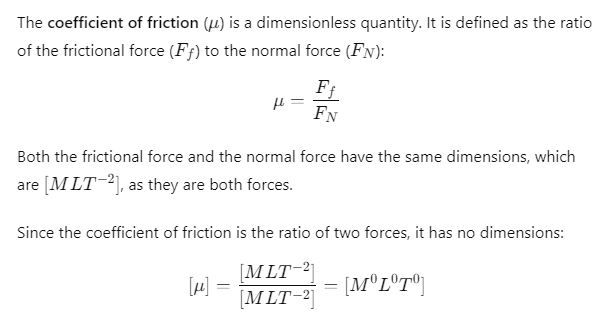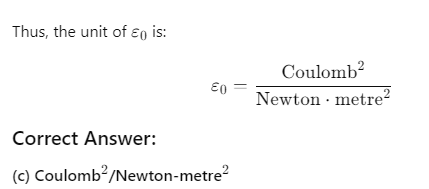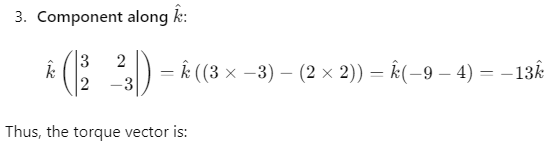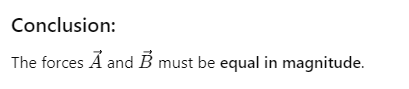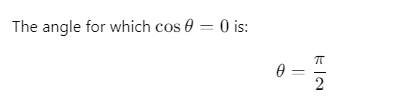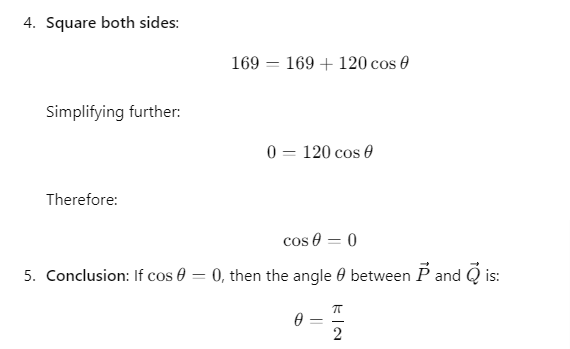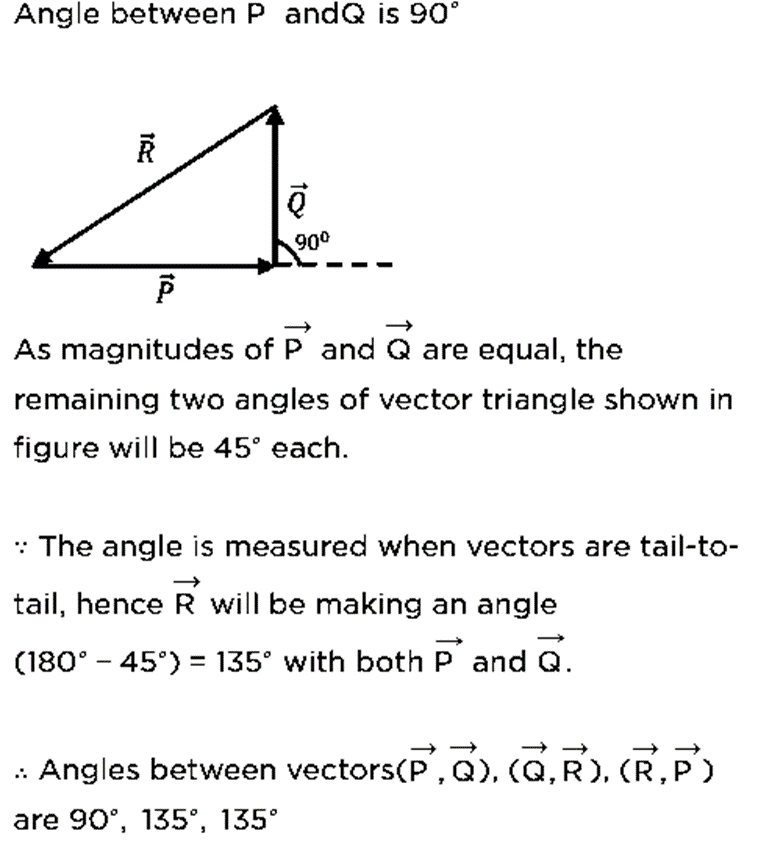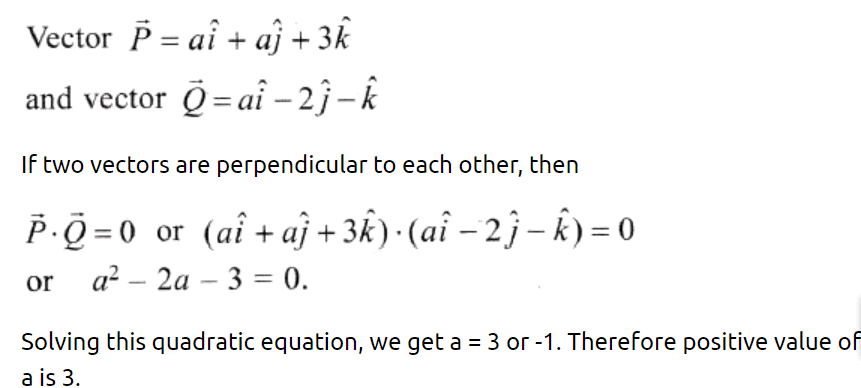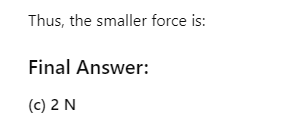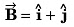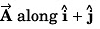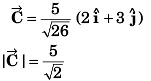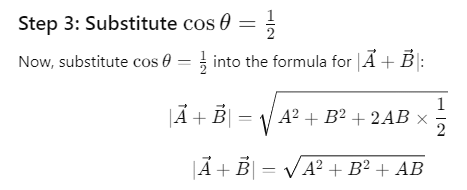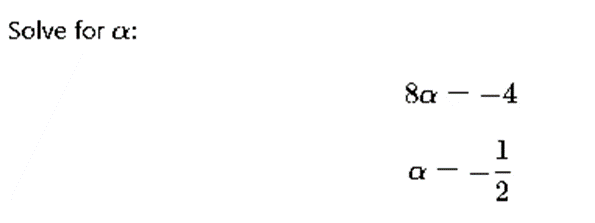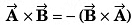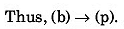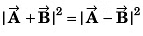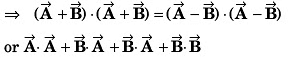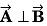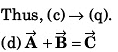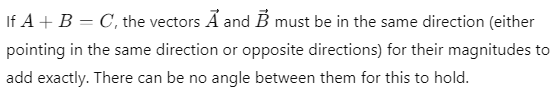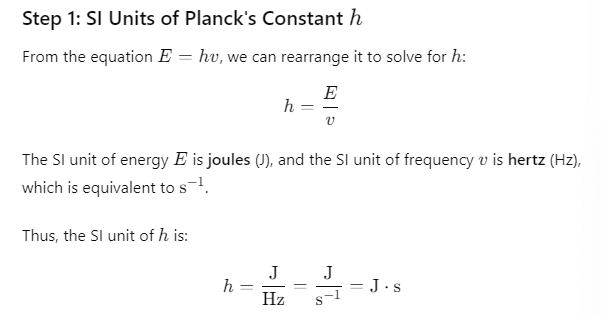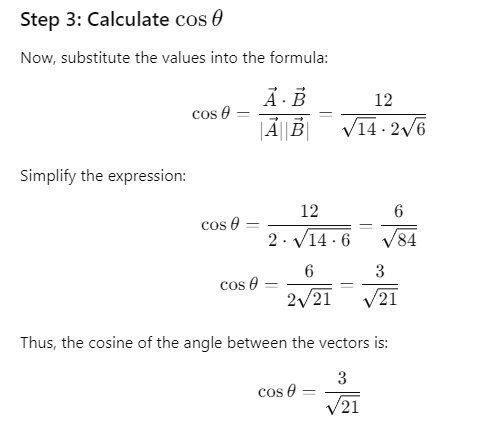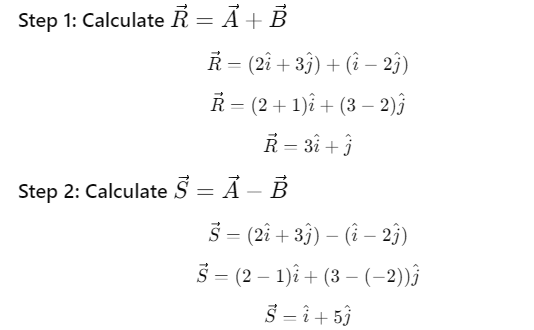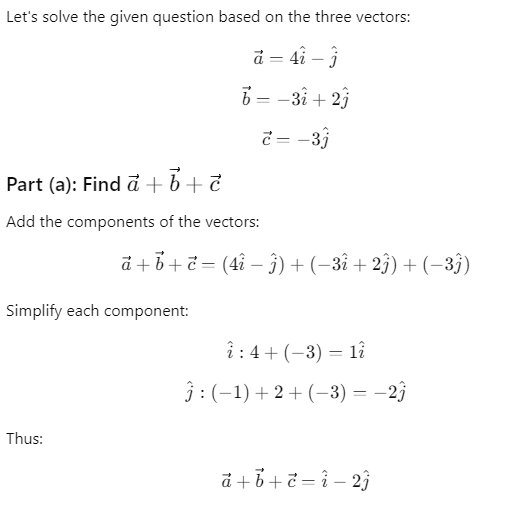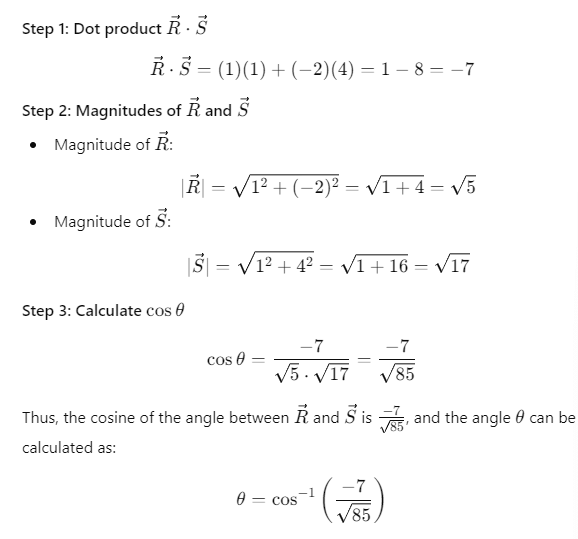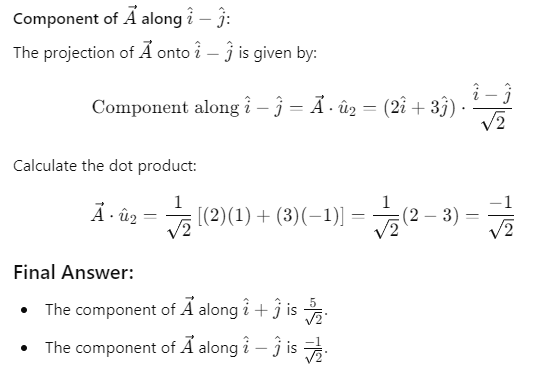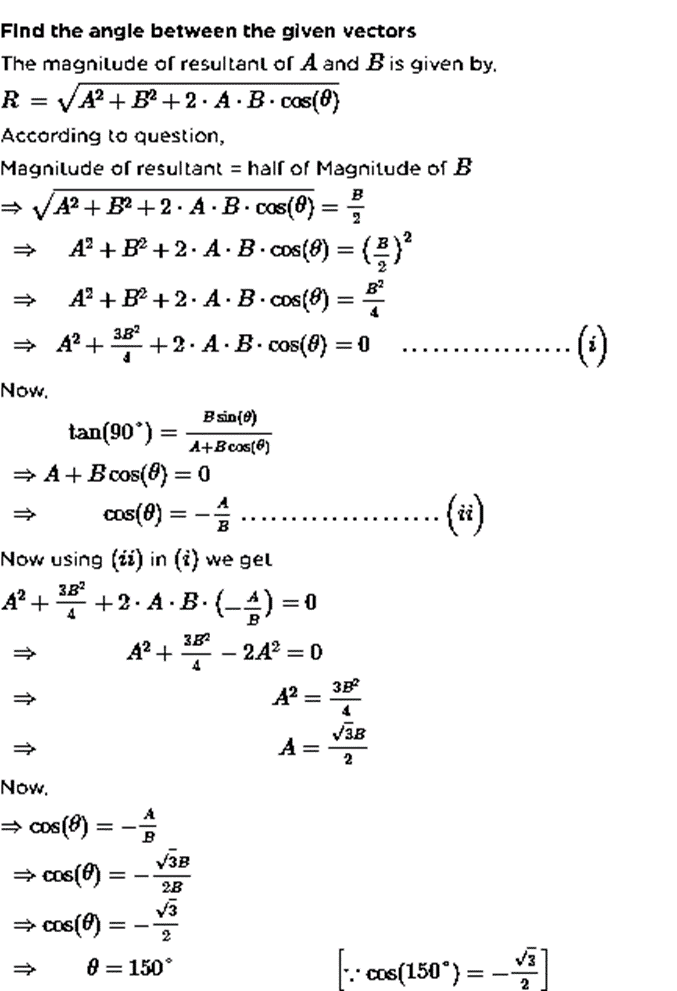DC Pandey Solutions: Units, Dimensions & Vectors | Physics Class 11 - NEET PDF Download
Section-I
Single Correct Option
Q.1. Which one of the following has the dimensions of pressure?
(a) [ML-2T-2]
(b) [M-1 L-1]
(c) [MLT-2]
(d) [ML-1T-2]
Ans: (d) [ML-1T-2]
Explanation:
Q.2. Which of the following will have the dimensions of time
(a) LC
(b) R/L
(c) L/R
(d) C/L
Ans: (c) L/R
Explanation:
Q.3. The force F on a sphere of radius a moving in a medium with velocity v is given by F = 6πηa v. The dimensions of-η are
(a) [ML-3]
(b) [MLT-2]
(c) [MT- 1]
(d) [ML-1T-1]
Ans: (d) [ML-1T-1]
Explanation:
Q.4. The dimensional formula for magnetic flux is
(a) [ML2T -2A-1]
(b) [ML3T-2A-2]
(c) [M0 L-2T-2A-2]
(d) [ML2T-1A2]
Ans: (a) [ML2T -2A-1]
Explanation:
Q.5. Dimensions of linear impulse are
(a) [ML-2T-3]
(b) [ML-2]
(c) [MLT -1]
(d) [MLT-2]
Ans. (c) [MLT -1]
Explanation:
Q.6. What is the dimensional formula of gravitational constant?
(a) [ML2T-2]
(b) [ML-1T -1]
(c) [M-1L3 T-2]
(d) None of these
Ans. (c) [M-1L3 T-2]
Explanation:
Q.7.Using mass (M), length (L), time (T) and current (A) as fundamental quantities, the dimension of permeability is
(a) [M-1LT-2A]
(b) [ML-2T-2A-1]
(c) [ML2T -2A-2]
(d) [MLT -1 A-1]
Ans. (c) [ML2T -2A-2]
Explanation:
Q.8. The equation of a wave is given by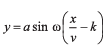 where ω is angular velocity and v is the linear velocity. The dimensions of k will be
where ω is angular velocity and v is the linear velocity. The dimensions of k will be
(a) [T2]
(b) [T-1]
(c) [T]
(d) [LT]
Ans. (c) [T]
Explanation:
Q.9. A force is given by F = at + bt2
where t is the time. The dimensions of a and b are
(a) [MLT -4] and [MLT 1]
(b) [MLT-1] and [MLT0]
(c) [MLT-3] and [MLT -4]
(d) [MLT -3] and [MLT0]
Ans. (c) [MLT-3] and [MLT -4]
Explanation:
Q.10. The dimensional formula for Planck’s constant and angular momentum are
(a) [ML2T-2] and [MLT-1]
(b) [ML2T-1] and [ML2T-1]
(c) [ML3T1] and [ML2T -2]
(d) [MLT-1] and [MLT-2]
Ans. (b) [ML2T-1] and [ML2T-1]
Explanation:
Q.11. If the energy (E), velocity (v) and force (F) be taken as fundamental quantities, then the dimensions of mass will be
(a) Fv-2 (b) Fv-1 (c) Ev-2 (d) Ev2
Ans. (c) Ev-2
Explanation:
Q.12. The dimension of  (ε0 is the permittivity of free space and E is electric field), is
(ε0 is the permittivity of free space and E is electric field), is
(a) [ML2T-1]
(b) [ML- 1T-2]
(c) [ML2T-2]
(d) [MLT-1]
Ans. (b) [ML- 1T-2]
Explanation:
Q.13. The dimensions of a/b in the equation 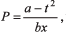 where P is pressure, x is distance and t is time, are
where P is pressure, x is distance and t is time, are
(a) [M2 LT -3]
(b) [MT-2]
(c) [LT-3]
(d) [ML3 T-1]
Ans. (b) [MT-2]
Explanation:
[a] = [T2]
∴
Q.14. Dimension of velocity gradient is
(a) [M°L°T-1]
(b) [ML- 1T-1]
(c) [M°LT-1]
(d) [ML°T-1]
Ans. (a) [M°L°T-1]
Explanation:
Q.15. If force F, length Land time T are taken as fundamental units, the dimensional formula for mass will be
(a) [FL- 1T2]
(b) [FLT-2]
(c) [FL- 1T-1]
(d) [FL5T2]
Ans: (a) [FL- 1T2]
Explanation:
Q.16. Which of the following is the dimension of the coefficient of friction?
(a) [M2 L2T]
(b) [M° L° T°]
(c) [ML2T-2]
(d) [M2 L2T-2]
Ans. (b) [M° L° T°]
Explanation:
Q.17. If C and R denote capacitance and resistance, then dimensions of CR will be
(a) [M°L°TA°]
(b) [ML°TA-2]
(c) [ML°TA2]
(d) [ML°T2A-2]
Ans: (a) [M°L°TA°]
Explanation:
Q.18. The unit of permittivity of free space, ε0 is
(a) Coulomb/newton-metre
(b) Newton-metre2/coulomb2
(c) Coulomb2/newton-metre2
(d) Coulomb2 /(newton -metre)2
Ans: (b) Newton-metre2 /coulomb2
Explanation:
Q.19. The ratio of the dimensions of Planck’s constant and that of the moment of inertia is the dimension of
(a) frequency
(b) velocity
(c) angular momentum
(d) time
Ans. (a) frequency
Explanation:
Q20. The velocity v of a particle at time t is given by 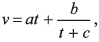 where a, b and c are constants. The dimensions of a, b and c are respectively
where a, b and c are constants. The dimensions of a, b and c are respectively
(a) [LT-2], [L] and [T]
(b) [L2], [T] and [LT2]
(c) [LT2], [LT] and [L]
(d) [L], [LT] and [T2]
Ans. (a) [LT-2], [L] and [T]
Explanation:
Q.21. Given that 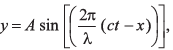 where y and x are measured in metres. Which of the following statements is true ?
where y and x are measured in metres. Which of the following statements is true ?
(a) The unit of λ is same as that of x and A
(b) The unit of λ, is same as that of x but not of A
(c) The unit of c is same as that of 2π/λ
(d) The unit of (ct - x) is same as that of 2π/λ
Ans. (a) The unit of λ is same as that of x and A
Explanation:
Q.22. The physical quantity having the dimensions [M-1L-3T3A2] is
(a) resistance
(b) resistivity
(c) electrical conductivity
(d) electromotive force
Ans. (a) resistance
Explanation:
Q.23. The torque of force 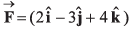 newton acting at the point
newton acting at the point  metre about origin is (in N-m)
metre about origin is (in N-m)
(a)
(b)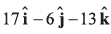
(c)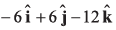
(d) 
Ans. (b) 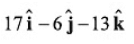
Explanation:
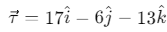
Q.24. If a unit vector is represented by 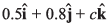 the value of c is
the value of c is
(a) 1
(b) √0.11
(c) √0.01
(d) 0.39
Ans: (b) 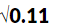
Explanation:
Q.25. 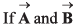 are two vectors such that
are two vectors such that 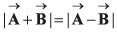 the angle between vectors
the angle between vectors 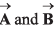 is
is
Ans. 90°
Explanation:
Q.26. The vector sum of two forces is perpendicular to their vector differences. In that case, the forces
(a) are not equal to each other in magnitude
(b) cannot be predicted
(c) are equal to each other
(d) are equal to each other in magnitude
Ans. (d) are equal to each other in magnitude
Explanation:
Q.27. Which one of the following is a scalar quantity?
(a) Displacement
(b) Electric field
(c) Acceleration
(d) Work
Ans: (d) Work
Explanation:
Q.28. Which one of the following is not the vector quantity?
(a) Torque
(b) Displacement
(c) Velocity
(d) Speed
Ans: (d) Speed
Explanation:
Q.29. What is the dot product of two vectors of magnitude 3 and 5, if angle between them is 60°?
(a) 5.2
(b) 7.5
(c) 8.4
(d) 8.6
Ans: (b) 7.5
Explanation:
Q.30. Two vectors 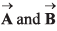 are such that
are such that 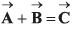 and A2 + B2 = C2.
and A2 + B2 = C2.
If 0 is the angle between positive direction of 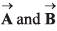 then the correct statement is
then the correct statement is
(a) θ = π
(b) θ = 2π/3
(c) θ = 0
(d) θ = π/2
Ans: (d) θ = π/2
Explanation:
Q31. Which one is a vector quantity?
(a) Time
(b) Temperature
(c) Flux density
(d) Magnetic field intensity
Ans: (d) Magnetic field intensity
Explanation:
Q32. Given that P = 12,Q = 5 and R =13 also 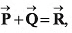 then the angle between
then the angle between 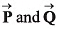 will be
will be
(a) π
(b) π/2
(c) zero
(d) π/4
Ans: (b) π/2
Explanation:
Q33. The forces, which meet at one point but their lines of action do not lie in one plane, are called
(a) non-coplanar non-concurrent forces
(b) non-coplanar concurrent forces
(c) coplanar concurrent forces
(d) coplanar non-concurrent forces
Ans: (b) non-coplanar concurrent forces
Explanation:
Q34. Given that 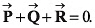 Two out of the three vectors are equal in magnitude. The magnitude of the third vector is √2 times that of the other two. Which of the following can be the angles between these vectors?
Two out of the three vectors are equal in magnitude. The magnitude of the third vector is √2 times that of the other two. Which of the following can be the angles between these vectors?
(a) 90°, 135°, 135°
(b) 45°, 45°, 90°
(c) 30°, 60°, 90°
(d) 45°, 90°, 135°
Ans: 90°, 135°, 135°
Explanation:
Q35. The angle between 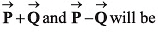
(a) 90°
(b) between 0° and 180°
(c) 180° only
(d) None of these
Ans: (b) between 0° and 180°
Explanation:
Q36. Two vectors of equal magnitude have a resultant equal to either of them, then the angle between them will be
(a) 30°
(b) 120°
(c) 60°
(d) 45°
Ans: (b) 120°
Explanation:
Let the two vectors be A and B, both having the same magnitude. The resultant of these vectors is given by:
Since the magnitude of the resultant is equal to the magnitude of either vector (A or B), we have:
Q37. A force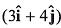 newton acts on a body and displaces it by
newton acts on a body and displaces it by 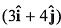 metre. The work done by the force is
metre. The work done by the force is
(a) 5 J
(b) 25 J
(c) 10 J
(d) 30 J
Ans: (b) 25 J
Explanation:
Q38. If the vectors 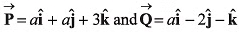 are perpendicular to each other then the positive value of a is
are perpendicular to each other then the positive value of a is
(a) zero
(b) 1
(c) 2
(d) 3
Ans: (d) 3
Explanation:
Q39. The angles which the vector 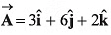 makes with the co-ordinate axes are
makes with the co-ordinate axes are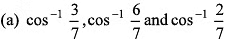
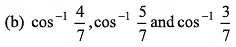
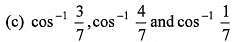
(d) none of the above
Ans: 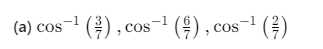
Explanation:
Q40. Unit vector parallel to the resultant of vectors 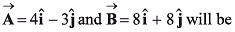
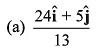
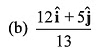
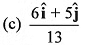
(d) None of these
Ans: (b) 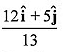
Explanation:
Q41. The value of n so that vectors 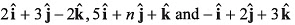 may be coplanar, will be
may be coplanar, will be
(a) 18
(b) 28
(c) 9
(d) 36
Ans: (a) 18
Explanation:
Q42. Which one of the following statement is false?
(a) A vector has only magnitude, whereas a scalar has both magnitude and direction
(b) Distance is a scalar quantity but displacement is a vector quantity
(c) Momentum, force, torque are vector quantities
(d) Mass, speed and energy are scalar quantities
Ans: (a) A vector has only magnitude, whereas a scalar has both magnitude and direction
Explanation:
Q43.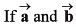 are two vectors then the value of
are two vectors then the value of 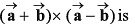
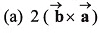
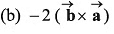
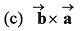
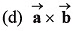
Ans: 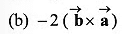
Explanation:
Q44. The angle between the two vectors 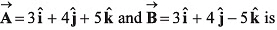
(a) 60°
(b) 0°
(c) 90°
(d) None of these
Ans: (c) 90°
Explanation:
Q45. Maximum and minimum values of the resultant of two forces acting at a point are 7 N and 3 N respectively. The smaller force will be equal to
(a) 5 N
(b) 4 N
(c) 2 N
(d) 1 N
Ans: 2 N
Explanation:
Q46. The component of vector 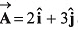 along the vector
along the vector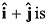
(a) 5/√2
(b) 10/√2
(c) 5 √2
(d) 5
Ans: 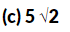
Explanation:
Angle betweenand
Component of
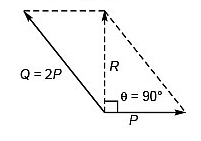
Q47. The resultant of two forces 3P and 2P is R. If the first force is doubled then the resultant is also doubled. The angle between the two forces is
(a) 60°
(b) 120°
(c) 70°
(d) 180°
Ans: (b) 120°
Explanation:
Q48. The resultant of two forces, one double the other in magnitude, is perpendicular to the smaller of the two forces. The angle between the two forces is
(a) 120°
(b) 60°
(c) 90°
(d) 150°
Ans: (a) 120°
Explanation:
Q49. Three vectors satisfy the relation 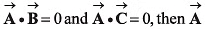 is parallel to
is parallel to
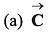
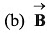
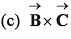
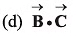
Ans: 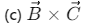
Explanation:

Q50. The sum of two forces at a point is 16 N. If their resultant is normal to the smaller force and has a magnitude of 8 N. Then two forces are
(a) 6N, 10N
(b) 8 N, 8 N
(c) 4 N, 12N
(d) 2 N, 14N
Ans: (a) 6N, 10N
Explanation:
Q51. then the value of
then the value of 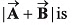
(a) (A2 + B2 + AB)1/2
(c) (A + B)

Ans: 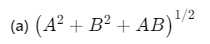
Explanation:
Q52. If the angle between the vectors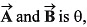 the value of the product
the value of the product 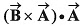 is equal to
is equal to
(a) BA2 cos θ
(b) BA2 sin θ
(c) BA2 sin θ cos θ
(d) zero
Ans: (d) zero
Explanation:
Q53. If a vector 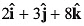 is perpendicular to the vector
is perpendicular to the vector 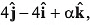 then the value of α is
then the value of α is
(a) -1
(b) 1/2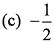
(d) 1
Ans: 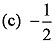
Explanation:
Q54. Minimum number of vectors of unequal magnitudes which can give zero resultant are
(a) two
(b) three
(c) four
(d) more than four
Ans: (b) three
Explanation:
The minimum number of vectors of unequal magnitudes that can give a zero resultant is determined by the fact that the vectors must form a closed geometric shape, where the sum of all the vectors equals zero.
Two vectors cannot give a zero resultant unless they are of equal magnitude and opposite direction, which contradicts the condition that the vectors must have unequal magnitudes.
Three vectors can give a zero resultant if they form a triangle. This is because the sum of the vectors' directions and magnitudes can balance each other out, resulting in a zero resultant.
Thus, the minimum number of vectors of unequal magnitudes required to give a zero resultant is three.
Q55. The (x, y, z) coordinates of two points A and B are given respectively as (0, 3, - 1) and (- 2, 6, 4). The displacement vector from A to B is given by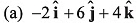
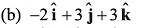
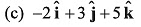

Ans: 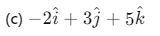
Explanation:
Q56. The sum of two vectors 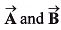 is at right angles to their difference. Then
is at right angles to their difference. Then
(a) A = B
(b) A = 2B
(c) B = 2A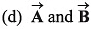
have the same direction.
Ans: (a) A = B
Explanation:
Match the Columns
Q1. Column-I shows some vector equations. Match column I with the value of the angle between A and B given in column II.
| Column I | Column II |
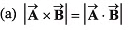 | (p) zero |
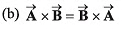 | (q) π/2 |
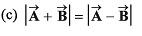 | (r) π/4 |
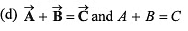 | (s) 3π/4 |
Ans:
Explanation:
or
or
⇒
Thus, (a) → (r) (s).
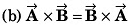
or
or sin θ = - sin θ
or 2 sin θ = 0
c)
⇒ θ = 0 rador
⇒
Section-II
Subjective Questions
Q1. Young’s modulus of steel is 2.0 x 1011 N / m2. Express it in dyne/cm2.
Sol:
Q2. Surface tension of water in the CGS system is 72 dynes/cm . What is its value in SI units
Sol:
Q3. In the expression y = a sin (ωt + θ), y is the displacement and t is the time. Write the dimensions of a, ω and θ.
Sol:
Q4. The relation between the energy E and the frequency v of a photon is expressed by the equation E = hv, where h is Planck’s constant. Write down the SI units of h and its dimensions.
Sol:
Q5. Write the dimensions of a and b in the relation.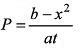
where P is power, x is distance and t is time.
Sol:
[b] = [x2] = [L2]
Q6. Check the correctness of the relation 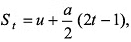 where u is initial velocity, a is acceleration and St is the displacement of by the body in tth second.
where u is initial velocity, a is acceleration and St is the displacement of by the body in tth second.
Sol:
Q7. Let x and a stand for distance. 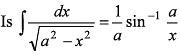 dimensionally correct?
dimensionally correct?
Sol:
Q8. In the equation 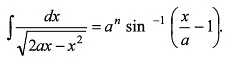 Find the value of n.
Find the value of n.
Sol:
Q9. Show dimensionally that the expression, 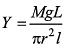 is dimensionally correct, where Y is Young’s modulus of the material of wire, L is length of wire, Mg is the weight applied on the wire and l is the increase in the length of the wire.
is dimensionally correct, where Y is Young’s modulus of the material of wire, L is length of wire, Mg is the weight applied on the wire and l is the increase in the length of the wire.
Sol:
Q10. The energy E of an oscillating body in simple harmonic motion depends on its mass m, frequency n and amplitude a. Using the method of dimensional analysis find the relation between E, m, n and a.
Sol:
Q11. The centripetal force F acting on a particle moving uniformly in a circle may depend upon mass (m), velocity (v) and radius r of the circle. Derive the formula for F using the method of dimensions.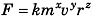
Sol:
Q12. Taking force F, length L and time T to be the fundamental quantities, find the dimensions of (a) density, (b) pressure, (c) momentum and (d) energy.
Sol:
Vectors
Q13. Find the cosine of the angle between the vectors 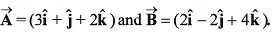
Sol:
Q14. Obtain the angle between 
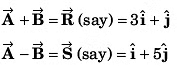 Angle between
Angle between  .
.
Sol:
Q15. Under what conditions will the vectors 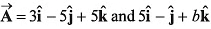 be perpendicular to each other ?
be perpendicular to each other ?
Sol:
Q16. Deduce the condition for the vectors 
Sol:
Q17. Three vectors which are coplanar with respect to a certain rectangular co-ordinate system are given by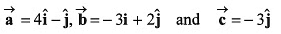 . Find
. Find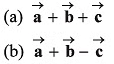
(c) Find the angle between 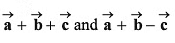
Sol:
Q18. Find the components of a vector 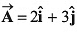 along the directions of
along the directions of 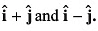
Sol:
Q19. If vectors 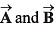 be respectively equal to
be respectively equal to 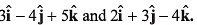 Find the unit vector parallel to resultant of
Find the unit vector parallel to resultant of 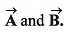
Sol:
Q20. If two vectors are 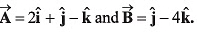 By calculation, prove that
By calculation, prove that
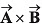 is perpendicular to both
is perpendicular to both 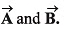
Sol:
Q21. The resultant of two vectors 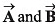 is at right angles to
is at right angles to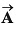 and its magnitude is half of
and its magnitude is half of 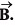 Find the angle between
Find the angle between 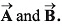
Sol:
Q22. The x and y-components of vector 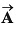 are 4 m and 6 m respectively. The x and y-components of vector
are 4 m and 6 m respectively. The x and y-components of vector  are 10 m and 9 m respectively. Calculate for the vector
are 10 m and 9 m respectively. Calculate for the vector 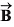 the following
the following
(a) its x and y-components
(b) its length
(c) the angle it makes with x-axis
Sol:
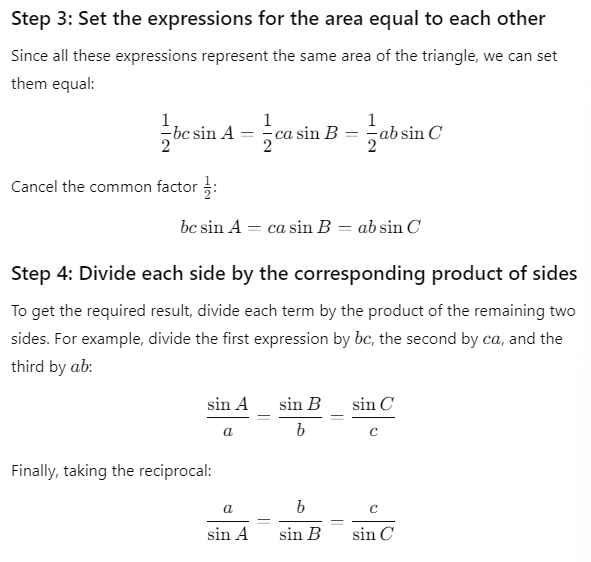
Q23. Prove by the method of vectors that in a triangle 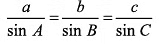
Sol:
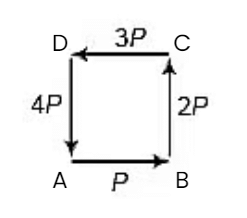
Q24. Four forces of magnitude P, 2P, 3P and AP act along the four sides of a square ABCD in cyclic order. Use the vector method to find the resultant force.
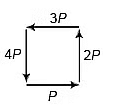
Sol:
Q25. 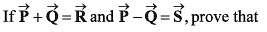 R2 + S2 = 2(P2 + Q2).
R2 + S2 = 2(P2 + Q2).
Sol:
|
96 videos|367 docs|98 tests
|
FAQs on DC Pandey Solutions: Units, Dimensions & Vectors - Physics Class 11 - NEET
| 1. What are the fundamental units used in physics according to DC Pandey's Solutions? |  |
| 2. How does DC Pandey explain the concept of dimensional analysis? |  |
| 3. What are the applications of vectors discussed in DC Pandey's Solutions? |  |
| 4. Can you explain the difference between scalar and vector quantities as per DC Pandey's content? |  |
| 5. What tips does DC Pandey provide for mastering units, dimensions, and vectors in competitive exams? |  |