DC Pandey Solutions: Units, Dimensions & Vectors - 3 - NEET PDF Download
Section-II
Subjective Questions
Ques 1: Young’s modulus of steel is 2.0 x 1011 N / m2. Express it in dyne/cm2.
Ans: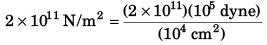
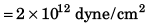
Ques 2: Surface tension of water in the CGS system is 72 dynes/cm . What is its value in SI units?
Ans: 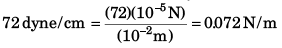
Ques 3: In the expression y = a sin (ωt + θ), y is the displacement and t is the time. Write the dim ensions of a, ω and θ.
Ans: [a] = [y] = [L]
Sol: [wt] = [M0L0 T0] ∴ [ω] = [T-1]
[θ] = [M0L0 T0]
Ques 4: The relation between the energy E and the frequency v of a photon is expressed by the equation E = hv, where h is Planck’s constant. Write down the SI units of h and its dimensions.
Ans: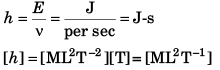
Ques 5: Write the dimensions of a and b in the relation.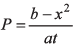
where P is power, x is distance and t is time.
Ans: [b] = [x2] = [L2]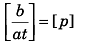

Ques 6: Check the correctness of the relation 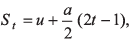 where u is initial velocity, a is acceleration and St is the displacement of by the body in tth second.
where u is initial velocity, a is acceleration and St is the displacement of by the body in tth second.
Ans: 
Here t in second. Hence the given equation seems to be dimensionally incorrect. But it is correct because 1 is hidden.
Ques 7: Let x and a stand for distance. 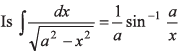 dim ensionally correct?
dim ensionally correct?
Ans: LHS is dimensionless. While RHS has the dimensions [L-1].
Ques 8: In the equation 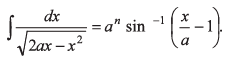
Find the value of n.
Ans: LHS is dimensionless. Hence n = 0.
Ques 9: Show dimensionally that the expression, 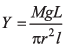 is dimensionally correct, where Y is Young’s modulus of the material of wire, L is length of wire, Mg is the weight applied on the wire and l is the increase in the length of the wire.
is dimensionally correct, where Y is Young’s modulus of the material of wire, L is length of wire, Mg is the weight applied on the wire and l is the increase in the length of the wire.
Ans: Just write the dimension of different physical quantities.
Ques 10: The energy E of an oscillating body in simple harmonic motion depends on its mass m, frequency n and amplitude a. Using the method of dimensional analysis find the relation between E, m, n and a.
Ans: E = kmxnyaz.
Here k = a dimensionless constant
∴ [E] = [m]x [n]y [a]z
∴ [ML2 T–2] = [M]x[T–1]y[L]z
∴ x = 1, y = 2 and z = 2
Ques 11: The centripetal force F acting on a particle moving uniformly in a circle may depend upon mass (m), velocity (v) and radius r of the circle. Derive the formula for F using the method of dimensions.
Ans: 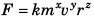
(k = a dimensionless constant) 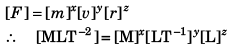
Solving we get,
x = 1, y = 2 and z = - 1
∴ 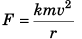
Ques 12: Taking force F, length L and time T to be the fundamental quantities, find the dimensions of (a) density, (b) pressure, (c) momentum and (d) energy.
Ans: [d] = [F]x [L]y [T]z
∴ [ML–3] = [MLT–2]x[L]y[T]z
Equating the powers we get,
x = 1, y = - 4, z = 2
∴ [ d] = [FL–4 T2]
Similarly other parts can be solved.
Vectors
Ques 13: Find the cosine of the angle between the vectors 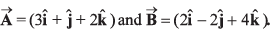
Ans: 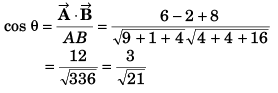
Ques 14: Obtain the angle between 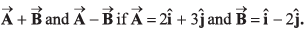
Ans: 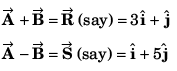
Angle between 
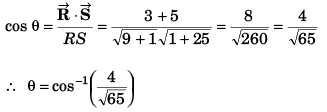
Ques 15: Under what conditions will the vectors 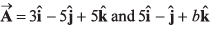 be perpendicular to each other ?
be perpendicular to each other ?
Ans: Their dot product should be zero.
Ques 16: Deduce the condition for the vectors 
Ans: Ratio of coefficients of 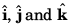 should be same.
should be same.
Ques 17: Three vectors which are coplanar with respect to a certain rectangular co-ordinate system are given by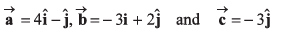
Find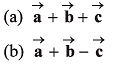
(c) Find the angle between 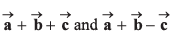
Ans: No solution is required.
Ques 18: Find the components of a vector 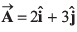 along the directions of
along the directions of
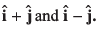
Ans: 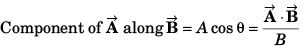
Ques 19: If vectors  be respectively equal to
be respectively equal to 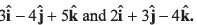 Find the unit vector parallel to
Find the unit vector parallel to 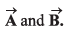
Ans:
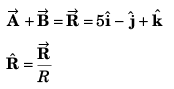
Ques 20: If two vectors are 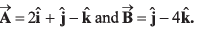 By calculation, prove that
By calculation, prove that
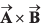 is perpendicular to both
is perpendicular to both 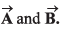
Ans: 
Ques 21: Find the area of the parallelogram whose sides are represented by 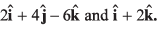
Ans: Area of parallelogram 
Ques 22: The resultant of two vectors 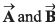 is at right angles to
is at right angles to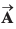 and its magnitude is half of
and its magnitude is half of 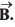 Find the angle between
Find the angle between 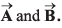
Ans: 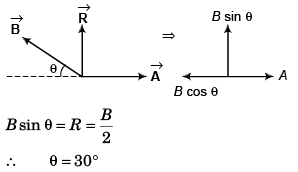

Ques 23: The x and y-components of vector 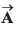 are 4 m and 6 m respectively. The x and y-components of vector
are 4 m and 6 m respectively. The x and y-components of vector 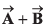 are 10 m and 9 m respectively. Calculate for the vector
are 10 m and 9 m respectively. Calculate for the vector 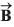 the following
the following
(a) its x andy-components
(b) its length
(c) the angle it makes with x-axis
Ans: 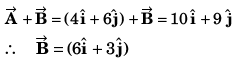
Ques 24: Prove by the method of vectors that in a triangle 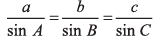
Ans: 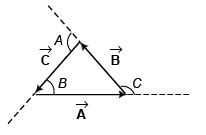
Applying sine law, we have

Ques 25: Four forces of magnitude P, 2P, 3P and AP act along the four sides of a square ABCDm cyclic order. Use the vector method to find the resultant force.
Ans: 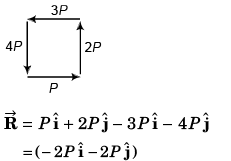
Ques 26: 
R2 + S2 = 2(P2 + Q2)
Ans: R2 = P2 + Q2 + 2PQ cos θ
S2 = P2 + Q2 - 2PQ cos θ
∴ R2 + S2 = 2 (P2 + Q2)
FAQs on DC Pandey Solutions: Units, Dimensions & Vectors - 3 - NEET
| 1. What are the basic units of measurement used in physics? |  |
| 2. How do you calculate dimensions of a physical quantity? |  |
| 3. What is a vector quantity? |  |
| 4. What are the operations that can be performed on vectors? |  |
| 5. How can vectors be resolved into components? |  |


















