Unit Test (Solutions): Arithmetic Progressions | Mathematics (Maths) Class 10 PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Q1: If a = 10 and d = 10, then first four terms will be: (1 Mark)
(a) 10, 30, 50, 60
(b) 10, 20, 30, 40
(c) 10, 15, 20, 25
(d) 10, 18, 20, 30
Ans: (b)
a = 10, d = 10
a1 = a = 10
a2 = a1+d = 10+10 = 20
a3 = a2+d = 20+10 = 30
a4 = a3+d = 30+10 = 40
Q2: 11th term of the A.P. -3, -1/2, 2 …. is (1 Mark)
(a) 28
(b) 22
(c) -38
(d) -48
Ans: (b)
A.P. = -3, -1/2, 2 …
First term a = – 3
Common difference, d = a2 − a1 = (-1/2) -(-3)
⇒ (-1/2) + 3 = 5/2
Nth term;
an = a+(n−1)d
a11 = 3+(11-1) (5/2)
a11 = 3+(10) (5/2)
a11 = -3+25
a11 = 22
Q3: Which term of the A.P. 3, 8, 13, 18, … is 78? (1 Mark)
Ans: 16
Given, 3, 8, 13, 18, … is the AP.
First term, a = 3
Common difference, d = a2 − a1 = 8 − 3 = 5
Let the nth term of given A.P. be 78. Now as we know,
an = a+(n−1)d
Therefore,
78 = 3+(n −1)5
75 = (n−1)5
(n−1) = 15
n = 16
Q4: The 21st term of AP whose first two terms are -3 and 4 is: (1 Mark)
(a) 17
(b) 137
(c) 143
(d) -143
Ans: (b)
First term = -3 and second term = 4
a = -3
d = 4-a = 4-(-3) = 7
a21=a+(21-1)d
=-3+(20)7
=-3+140
=137
Q5: What is the common difference of an A.P. in which a21 – a7 = 84? (1 Mark)
Ans: 6
a21 – a7 = 84 …[Given]
∴ (a + 20d) – (a + 6d) = 84 …[an = a + (n – 1)d
20d – 6d = 84
14d = 84
⇒ d = 84/14
d = 6
Q6: The angles of a triangle are in A.P., the least being half the greatest. Find the angles. (2 Marks)
Ans: Let the angles be a – d, a, a + d; a > 0, d > 0
∵ Sum of angles = 180°
∴ a – d + a + a + d = 180°
⇒ 3a = 180° ∴ a = 60° …(i)
By the given condition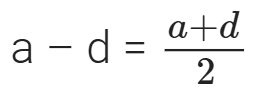 ⇒ 2 = 2a – 2d = a + d
⇒ 2 = 2a – 2d = a + d
⇒ 2a – a = d + 2d ⇒ a = 3d 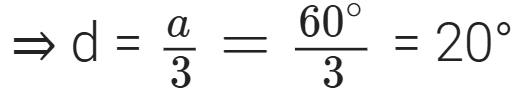 … [From (i)
… [From (i)
∴ Angles are: 60° – 20°, 60°, 60° + 20°
i.e., 40°, 60°, 80°
Q7: Find whether -150 is a term of the A.P. 17, 12, 7, 2, …? (2 Marks)
Ans: Given: 1st term, a = 17
Common difference, d = 12 – 17 = -5
nth term, an = – 150 (Let)
∴ a + (n – 1) d = – 150
17 + (n – 1) (-5) = – 150
(n – 1) (-5) = – 150 – 17 = – 167 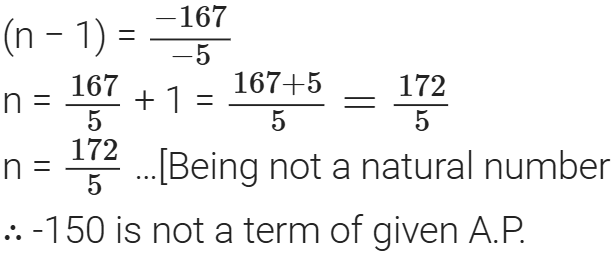
Q8: The 4th term of an A.P. is zero. Prove that the 25th term of the A.P. is three times its 11thterm. (2 Marks)
Ans: Let 1st term = a, Common difference = d
a4 = 0 a + 3d = 0 ⇒ a = -3d … (i)
To prove: a25 = 3 × a11
a + 24d = 3(a + 10d) …[From (i)
⇒ -3d + 24d = 3(-3d + 10d)
⇒ 21d = 21d
From above, a25 = 3(a11)
Hence proved, the 25th term of the A.P. is three times its 11th term.
Q9: The 19th term of an AP is equal to three times its 6th term. If its 9th term is 19, find the A.P. (3 Marks)
Ans: Let in an A.P. first term = a, Common difference = d
T₉ = 19
a + 8d = 19 — — — (1)
Given,
T₉ = 3T₆
⇒ a + 18d = 3(a + 5d)
⇒ a + 18d = 3a + 15d
⇒ 0 = 3a + 15d – a – 18d
⇒ 2a – 3d = 0 — — — (2)
Subtract (2) from (1)
⇒ –19d = –38
⇒ d = 2
substitute d = 2 in (1)
⇒ a = 3
therefore a = 3, d = 2
required AP is 3, 5, 7, 9, ....
Q10: If the seventh term of an AP is 1/9 and its ninth term is 1/7, find its 63rd term. (3 Marks)
Ans: Let a be the first term and d be the common difference of the given AP.
Then,
T₇ = 1/9 ⇒ a + 6d = 1/9
...(i)
T₉ = 1/7 ⇒ a + 8d = 1/7
...(ii)
On subtracting (i) form (ii), we get
2d = (1/7 − 1/9) = 2/63 ⇒ d = (1/2 × 2/63) = 1/63.
Putting d = 1/63 in (i), we get
a + (6 × 1/63) = 1/9 ⇒ a + 2/21 = 1/9 ⇒ a
= (1/9 − 2/21) = (7 − 6/63) = 1/63
Thus, a = 1/63 and d = 1/63.
∴ T₆₃ = a + (63 − 1)d = (a + 62d)
= (1/63 + 62 × 1/63) = (1/63 + 62/63) = 1.
Hence, 63rd term of the given AP is 1.
Q11: The digits of a positive number of three digits are in A.P. and their sum is 15. The number obtained by reversing the digits is 594 less than the original number. Find the number. (3 Marks)
Ans:
Let hundred’s place digit = (a – d)
Let ten’s place digit = a
Let unit’s place digit = a + d
According to the Question,
a – d + a + a + d = 15
⇒ 3a = 15 ⇒ a = 5
Original number
= 100(a – d) + 10(a) + 1(a + d)
= 100a – 100d + 10a + a + d
= 111a – 99d
Reversed number
= 1(a – d) + 10a + 100(a + d)
= a – d + 10a + 100a + 100d
= 111a + 99d
Now, Original no. – Reversed no. = 594
111a – 99d – (111a + 99d) = 594 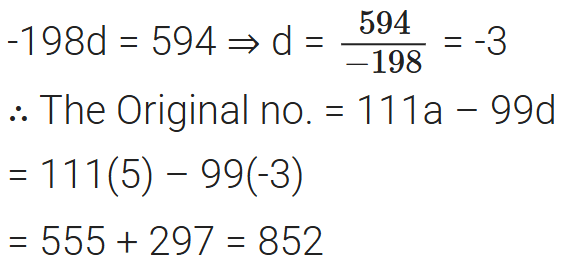
Q12: A manufacturer of TV sets produced 800 sets in the third year and 1000 sets in the seventh year. Assuming that the production increases uniformly by a fixed number every year, find: (5 Marks)
(i) the production in the 1st year
(ii) the production in the 10th year
(iii) the total production in the first 7 years
Ans: Since the production increases uniformly by a fixed number every year, the number of TV sets manufactured in the 1st, 2nd, 3rd, ... years will form an AP.
Let us denote the number of TV sets manufactured in the nth year by an.
Given:
Then,
Solving these two equations:
Subtracting the first equation from the second:
Now substitute d=50 into the first equation:
(i) Production of TV sets in the 1st year is
(ii) Production in the 10th year:
So, the production in the 10th year is 1150 TV sets.
(iii) Total production in the first 7 years: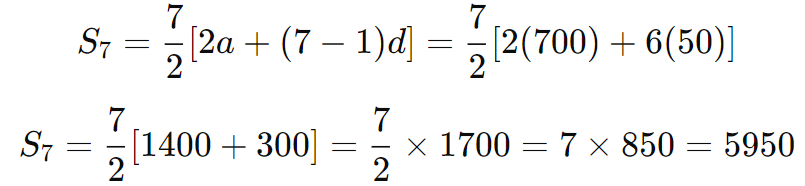 Thus, the total production of TV sets in the first 7 years is 5950.
Thus, the total production of TV sets in the first 7 years is 5950.
Q13: A sum of ₹1,600 is to be used to give ten cash prizes to students of a school for their overall academic performance. If each prize is ₹20 less than its preceding prize, find the value of each of the prizes. (5 Marks)
Ans: Here S10 = 1600, d = -20, n = 10 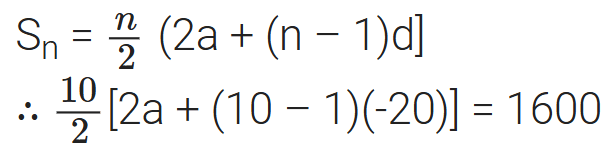 2a – 180 = 320
2a – 180 = 320
2a = 320 + 180 = 500
a = 250
∴ 1st prize = a = ₹250
2nd prize = a2 = a + d = 250 + (-20) = ₹230
3rd prize = a3 = a2 + d = 230 – 20 = ₹210
4th prize = a4 = a3 + d = 210 – 20 = ₹190
5th prize = a5 = a4 + d = 190 – 20 = ₹170
6th prize = a6 = a5 + d = 170 – 20 = ₹150
7th prize = a7 = a6 + d = 150 – 20 = ₹130
8th prize = a8 = a7 + d = 130 – 20 = ₹110
9th prize = a9 = a8 + d = 110 – 20 = ₹590
10th prize = a10 = a9 + d = 90 – 20 = ₹70
= ₹ 1,600
|
127 videos|685 docs|84 tests
|
FAQs on Unit Test (Solutions): Arithmetic Progressions - Mathematics (Maths) Class 10
| 1. What is an arithmetic progression? |  |
| 2. How do you find the nth term of an arithmetic progression? |  |
| 3. How can arithmetic progressions be used in real life? |  |
| 4. What is the sum of the first n terms of an arithmetic progression? |  |
| 5. How can you identify if a sequence of numbers is an arithmetic progression? |  |
















