Unit Test (Solutions): Triangles | Mathematics (Maths) Class 10 PDF Download

Time: 1 hour

M.M. 30

Attempt all questions.

• Question numbers 1 to 5 carry 1 mark each.
• Question numbers 6 to 8 carry 2 marks each.
• Question numbers 9 to 11 carry 3 marks each.
• Question number 12 & 13 carry 5 marks each.

Q1. In ΔPQR, if PS is the internal bisector of ∠P meeting QR at S and PQ = 15 cm, QS = (3 + x) cm, SR = (x – 3) cm and PR = 7 cm, then find the value of x. (1 Mark)
(a) 2.85 cm
(b) 8.25 cm
(c) 5.28 cm
(d) 8.52 cm

Ans: (b)

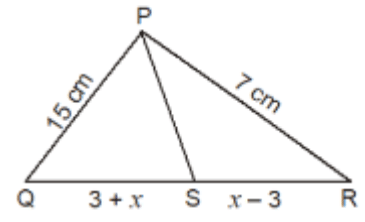
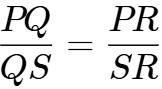
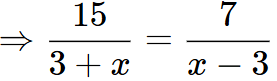
Since PS is the internal bisector of ∠P and it meets QR at S image.

∴

⇒ 7(3+x) = 15(x–3)

⇒ 21+7x = 15x–45

⇒ 15x–7x = 45+21

⇒ 8x = 66

⇒ 4x = 33

⇒ x = 8.25cm

Q2: If ABC and DEF are two triangles and AB/DE=BC/FD, then the two triangles are similar if
(a) ∠A=∠F
(b) ∠B=∠D
(c) ∠A=∠D
(d) ∠B=∠E

Ans: (b)

If ABC and DEF are two triangles and AB/DE=BC/FD, then the two triangles are similar if ∠B=∠D.

Q3: If in two triangles ABC and PQR, AB/QR = BC/PR = CA/PQ, then
(a) ΔPQR ~ ΔCAB 
(b) ΔPQR ~ ΔABC
(c) ΔCBA ~ ΔPQR 
(d) ΔBCA ~ ΔPQR

Ans: (a)

Given that, in triangles ABC and PQR, AB/QR = BC/PR = CA/PQ

If sides of one triangle are proportional to the side of the other triangle, and their corresponding angles are also equal, then both the triangles are similar by SSS similarity. Therefore, ΔPQR ~ ΔCAB.

Q4: In △ABC, AD is the median. If △ABD ~ △ACD, then △ABC is _______________________.

Ans: Isosceles triangle

In triangle △ABC, AD is the median, meaning that it divides side BC into two equal parts, BD = DC. If △ABD is similar to △ACD, it implies that the two triangles have the same shape, meaning their corresponding angles are equal and the sides are proportional.

Since △ABD and △ACD are similar, and the sides BD and DC are equal (as AD is the median), it follows that the corresponding sides AB and AC must also be equal. Therefore, △ABC is an isosceles triangle, where AB = AC.

Q5: D and E are respectively the points on sides AB and AC of triangle ABC such that AB = 3 cm, BD = 1.5 cm, BC = 7.5 cm, and DE || BC. What is the length of DE?
(a) 2 cm
(b) 2.5 cm
(c) 3.75 cm
(d) 3 cm

Ans: (c)

Since DE∥BC, by the Basic Proportionality Theorem (Thales' Theorem), the triangles $\backslash triangle\; ADE$△ADE and △ABC are similar. This means the corresponding sides are proportional.
The ratio of the sides is given by: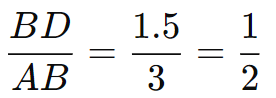  
Since DE∥BC, the length of DE will be proportional to BC: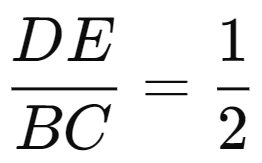

Given BC=7.5cm, we can calculate the length of DE:

DE = 1/2 X 7.5 = 3.75 

Thus, the length of DE is 3.75 cm.

Q6: In the figure, DE // AC and DF // AE. Prove that BF/FE = BE/EC. (2 Marks)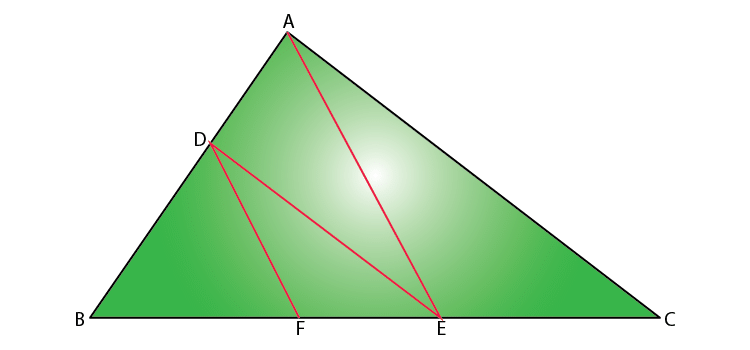

Ans:

Given that,

In triangle ABC, DE // AC.

By Basic Proportionality Theorem,

BD/DA = BE/EC……….(i)

Also, given that DF // AE.

Again by Basic Proportionality Theorem,

BD/DA = BF/FE……….(ii)

From (i) and (ii),

BE/EC = BF/FE

Hence, proved.

Q7: In the figure, DE || BC. Find the length of side AD, given that AE = 1.8 cm, BD = 7.2 cm and CE = 5.4 cm. (2 Marks)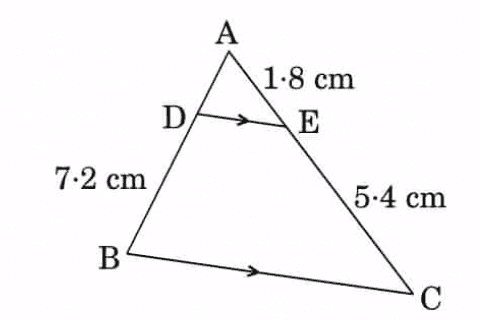

Ans: Given, DE || BC

AE = 1.8 cm, BD = 7.2 cm and CE = 5.4 cm

By basic proportionality theorem,

AD/DB = AE/EC

AD/7.2 = 1.8/5.4

AD = (1.8 × 7.2)/5.4

= 7.2/4

= 2.4

Therefore, AD = 2.4 cm.

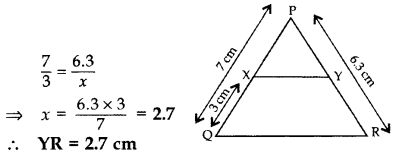
Q8: In the given figure, XY || QR,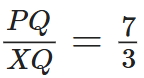 and PR = 6.3 cm, find YR. (2 Marks)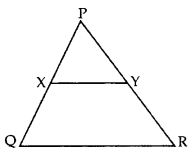

Ans: Let YR = x 
..... Thales Theorem

Q9: D and E are points on sides AB and AC of triangle ABC such that DE || BC. If AD = 2·4 cm, DB = 3.6 cm and AC = 5 cm, find AE. (3 Marks) 

Ans: Given, DE || BC,  AD = 2.4 cm, DB = 3.6 cm and AC = 5 cm

In ABC, DE || BC

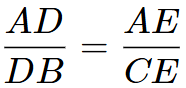∴ (by basic proportionality theorem)

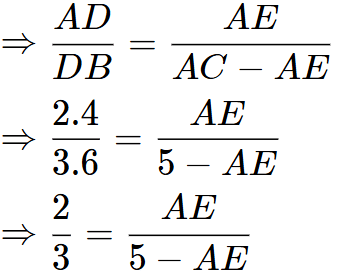
⇒3AE + 2AE = 10

⇒3AE = 10 − 2AE

⇒AE = 10/5

⇒AE = 2cm

Q10: X and Y are points on the sides AB and AC respectively of a triangle ABC such that 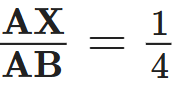, AY = 2 cm and YC = 6 cm. Find whether XY || BC or not. (3 Marks)

Ans: 

Given,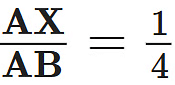

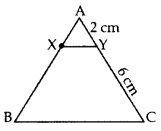
AX = 1K, AB = 4K
∴ BX = AB – AX
= 4K – 1K = 3K 

∴ XY || BC … [By converse of Thales’ theorem 

Q11: If a line segment intersects sides AB and AC of a ∆ABC at D and E respectively and is parallel to BC, prove that. (3 Marks)

Ans: Given. In ∆ABC, DE || BC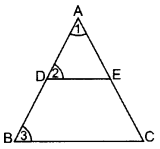

Proof.

In ∆ADE and ∆ABC

∠1 = ∠1 … Common

∠2 = ∠3 … [Corresponding angles]

∆ADE ~ ∆ABC …[AA similarity]

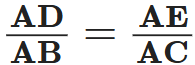∴ …[In ~∆s corresponding sides are proportional]

Q12: In the given figure, altitudes AD and CE of ∆ ABC intersect each other at the point P. Show that: (5 Marks)
(i) ∆AEP ~ ∆ CDP
(ii) ∆ABD ~ ∆ CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆ PDC ~ ∆ BEC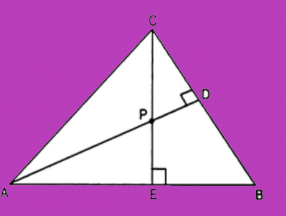

Ans: 

Given that AD and CE are the altitudes of triangle ABC and these altitudes intersect each other at P.

(i) In ΔAEP and ΔCDP,

∠AEP = ∠CDP (90° each)

∠APE = ∠CPD (Vertically opposite angles)

Hence, by AA similarity criterion,

ΔAEP ~ ΔCDP

(ii) In ΔABD and ΔCBE,

∠ADB = ∠CEB ( 90° each)

∠ABD = ∠CBE (Common Angles)

Hence, by AA similarity criterion,

ΔABD ~ ΔCBE

(iii) In ΔAEP and ΔADB,

∠AEP = ∠ADB (90° each)

∠PAE = ∠DAB (Common Angles)

Hence, by AA similarity criterion,

ΔAEP ~ ΔADB

(iv) In ΔPDC and ΔBEC,

∠PDC = ∠BEC (90° each)

∠PCD = ∠BCE (Common angles)

Hence, by AA similarity criterion,

ΔPDC ~ ΔBEC

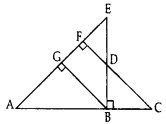
Q13: In given figure, EB ⊥ AC, BG ⊥ AE and CF ⊥ AE. (5 Marks)
Prove that:
(a) ∆ABG ~ ∆DCB

(b)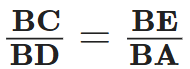 

Ans: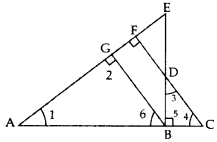 

Given: EB ⊥ AC, BG ⊥ AE and CF ⊥ AE.

To prove: (a) ∆ABG – ∆DCB,

(b)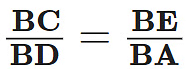 

Proof: (a) In ∆ABG and ∆DCB,
∠2 = ∠5 … [each 90°
∠6 = ∠4 … [corresponding angles
∴ ∆ABG ~ ∆DCB … [By AA similarity
(Hence Proved)
∴ ∠1 = ∠3 …(CPCT … [In ~∆s, corresponding angles are equal

(b) In ∆ABE and ∆DBC,
∠1 = ∠3 …(proved above
∠ABE = ∠5 … [each is 90°, EB ⊥ AC (Given)
∆ABE ~ ∆DBC … [By AA similarity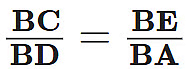
… [In ~∆s, corresponding sides are proportional ]

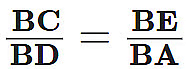∴... Hence, Proved.