Class 10 Exam > Class 10 Notes > Mathematics (Maths) Class 10 > Unit Test: Introduction to Trigonometry
Unit Test: Introduction to Trigonometry | Mathematics (Maths) Class 10 PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Q1: When cos A = 4/5, the value for tan A is (1 Mark)
(a) 3/5
(b) 3/4
(c) 5/3
(d) 4/3
Q2: Which of the following is the the simplest value of cos² θsin θ + sin θ (1 Mark)
(a) cosec θ
(b) sec θ
(c) sinθ
(d) cosine θ
Q3: True/ False (1 Mark)
tan θ = sin θ / cos θ
Q4: True/ False (1 Mark)
The value of sin 30° is greater than the value of sin 60°.
Q5: True/ False (1 Mark)
The cosine of an angle is the ratio of the opposite side to the adjacent side in a right triangle.
Q6: Evaluate cos 60° sin 30° + sin 60° cos 30°1
Q7: Prove that : 2cos² θ - 1cos⁴ θ - 2sin² θ + 1sin⁴ θ = cot⁴ θ - tan⁴ θ (2 Marks)
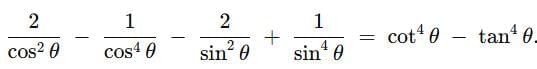
Q8: If 7sin2θ + 3cos2θ = 4, then find the value of tan θ. (2 Marks)
Q9: When sec 4A = cosec (A – 20°), here 4A is an acute angle, find out the value of A. (3 Marks)
Q10: If 3x = sec θ and 9 x² - 1x² = tan θ, then find the value.(3 Marks)
Q11: If ∠A and ∠B are the acute angles such that cos A = cos B, then show that ∠ A = ∠ B. (3 Marks)
Q12: In triangle ABC, right-angled at B, when tan A = 1/√3 find out the value : (5 marks)
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Q13: In ∆ ABC, the right-angled at B, AB = 24 cm, BC = 7 cm. Determine: (5 Marks)
(i) sin A, cos A
(ii) sin C, cos C
You can find the solutions of this Unit Test here: Unit Test (Solutions): Introduction to Trigonometry
The document Unit Test: Introduction to Trigonometry | Mathematics (Maths) Class 10 is a part of the Class 10 Course Mathematics (Maths) Class 10.
All you need of Class 10 at this link: Class 10
|
127 videos|585 docs|79 tests
|
FAQs on Unit Test: Introduction to Trigonometry - Mathematics (Maths) Class 10
| 1. What are the basic trigonometric ratios and how are they defined? |  |
Ans. The basic trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). They are defined based on a right triangle:
- Sine is the ratio of the length of the opposite side to the length of the hypotenuse (sin = opposite/hypotenuse).
- Cosine is the ratio of the length of the adjacent side to the length of the hypotenuse (cos = adjacent/hypotenuse).
- Tangent is the ratio of the length of the opposite side to the length of the adjacent side (tan = opposite/adjacent).
| 2. How do you find the values of trigonometric functions for common angles? | |
Ans. The values of trigonometric functions for common angles (0°, 30°, 45°, 60°, and 90°) can be found using the unit circle or special right triangles. For example:
- sin(0°) = 0, cos(0°) = 1, tan(0°) = 0
- sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = 1/√3
- sin(45°) = √2/2, cos(45°) = √2/2, tan(45°) = 1
- sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3
- sin(90°) = 1, cos(90°) = 0, tan(90°) is undefined.
| 3. What is the Pythagorean theorem and how does it relate to trigonometry? | |
Ans. The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). It can be expressed as a² + b² = c². This theorem is fundamental in trigonometry as it relates to the definitions of the sine, cosine, and tangent functions, which can be derived from the sides of a right triangle based on this relationship.
| 4. What is the difference between radians and degrees in trigonometry? | |
Ans. Radians and degrees are two units for measuring angles. Degrees divide a circle into 360 equal parts, while radians are based on the radius of the circle; one radian is the angle formed when the arc length is equal to the radius. To convert degrees to radians, you can use the formula: radians = degrees × (π/180). Conversely, to convert radians to degrees, use: degrees = radians × (180/π).
| 5. How can trigonometric functions be applied in real-life scenarios? | |
Ans. Trigonometric functions have various real-life applications, including:
- Engineering: calculating forces, angles, and distances in structures.
- Physics: analyzing waves, oscillations, and periodic motion.
- Navigation: determining positions and distances using angles.
- Architecture: designing buildings with specific angles and heights.
- Computer graphics: creating realistic animations and simulations using angles and distances.
About this Document
3K Views
4.71/5
Rating
Dec 06, 2025
Last updated
Related Exams
Document Description: Unit Test: Introduction to Trigonometry for Class 10 2025 is part of Mathematics (Maths) Class 10 preparation.
The notes and questions for Unit Test: Introduction to Trigonometry have been prepared according to the Class 10 exam syllabus. Information about Unit Test: Introduction to Trigonometry covers topics
like and Unit Test: Introduction to Trigonometry Example, for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Unit Test: Introduction to Trigonometry.
Introduction of Unit Test: Introduction to Trigonometry in English is available as part of our Mathematics (Maths) Class 10
for Class 10 & Unit Test: Introduction to Trigonometry in Hindi for Mathematics (Maths) Class 10 course.
Download more important topics related with notes, lectures and mock test series for Class 10
Exam by signing up for free. Class 10: Unit Test: Introduction to Trigonometry | Mathematics (Maths) Class 10
Description
Full syllabus notes, lecture & questions for Unit Test: Introduction to Trigonometry | Mathematics (Maths) Class 10 - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 10 | Best notes, free PDF download
Information about Unit Test: Introduction to Trigonometry
In this doc you can find the meaning of Unit Test: Introduction to Trigonometry defined & explained in the simplest way possible. Besides explaining types of
Unit Test: Introduction to Trigonometry theory, EduRev gives you an ample number of questions to practice Unit Test: Introduction to Trigonometry tests, examples and also practice Class 10
tests
Related Searches