Universal Law of Gravitation | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Newton’s Law Of Universal Gravitation |

|
| Properties of Gravitational Force |

|
| Gravitation Equation Vector Form |

|
| Mass and Weight |

|
| Is the force of Gravity the same all over the Earth? |

|
In the 1600s, an English physicist and mathematician named Isaac Newton was sitting under an apple tree. Apparently, an apple fell on his head, and he started wondering why the apple was attracted to the ground in the first place. Today we all know that it happened due to the force of gravitation.
Newton’s Law Of Universal Gravitation
Newton’s Law of Universal Gravitation states that every particle attracts every other particle in the universe with a force that is directly proportional to the product of the masses and inversely proportional to the square of the distance between them.
The universal gravitation equation thus takes the form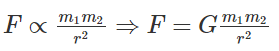
 Law of Gravitation
Law of Gravitation
where F is the gravitational force between bodies, m1 is the mass of one of the objects, m2 is the mass of the second object, r is the distance between the centers of two objects, and G is the universal gravitational constant.
The constant proportionality (G) in the above equation is known as the universal gravitation constant. Henry Cavendish experimentally determined the precise value of G.
The value of G is found to be G = 6.674 × 10-11 N m2/kg2.
Properties of Gravitational Force
- The gravitational force is a conservative force, operating along the line joining the centers of two masses, which qualifies it as a central force.
- It remains unaffected by the medium between the two objects, as well as the characteristics and dimensions of the objects themselves.
- This force complies with Newton's third law of motion, forming an action-reaction pair, and it remains unaltered by the presence or absence of other bodies in the surrounding environment.
Gravitation Equation Vector Form
The universal gravitation equation is represented in vector form as follows:
where G is the gravitational constant and 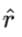 is the unit vector from m1 to m2. The figure below shows the gravitational force on m1 due to m2 is along the direction of
is the unit vector from m1 to m2. The figure below shows the gravitational force on m1 due to m2 is along the direction of 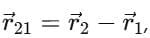 a unit vector pointing from m1 to m2.
a unit vector pointing from m1 to m2.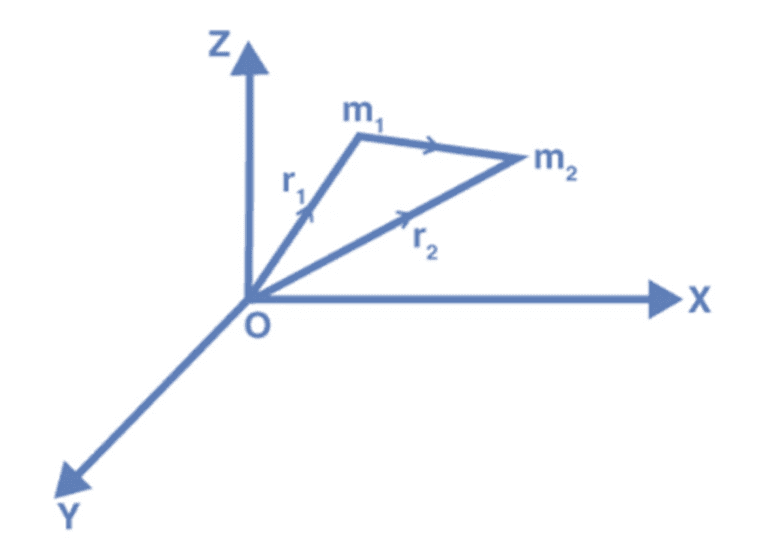
If we have a collection of point masses, the force on any one of them is the vector sum of the gravitational forces exerted by the other point masses: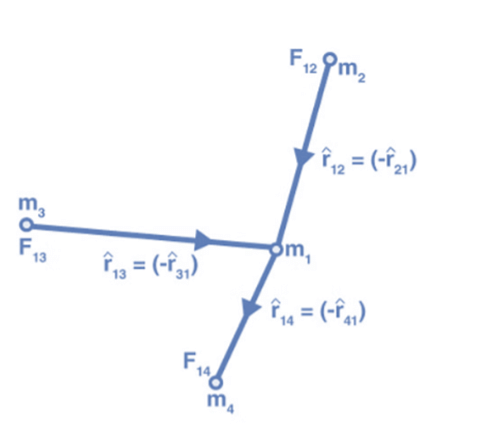
The gravitational force on point mass m1 is the vector sum of the gravitational forces exerted by m2, m3 and m4. Therefore, the total force on m1 is given by: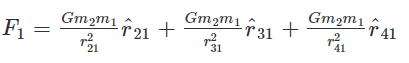
Example 1: Calculate the gravitational force of attraction between the Earth and a 70 kg man standing at sea level, a distance of 6.38 x 106 m from the Earth’s center.
Solution: Given,
m1 is the mass of the Earth = 5.98 x 1024 kg
m2 is the mass of the man = 70 kg
r = 6.38 x 106 m
The value of G = 6.674 x 10-11 N m2/kg2
Now, substituting the values in the Gravitational force formula, we get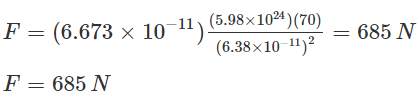
Example 2: A sphere of mass 100 kg is attracted by another spherical mass of 11.75 kg by a force of 19.6 x 10-7 N when the distance between their centers is 0.2 m. Find G.
Solution: Mass of first body = m1 = 100 kg, mass of second body = m2 = 11.75 kg, distance between masses = r = 0.2 m, force between them = F = 19.6 x 10-7 N,
To find: The gravitational constant G
By Newton’s law of gravitation, The value of the universal gravitation constant is 6.672 x 10-11 N m2/kg2.
The value of the universal gravitation constant is 6.672 x 10-11 N m2/kg2.
Example 3: Calculate the gravitational force of attraction between two metal spheres each of mass 90 kg, if the distance between their centers is 40 cm. Given G = 6.67 x 10-11 N m2/kg2. Will the force of attraction be different if the same bodies are taken on the moon, their separation remaining the same?
Solution: Mass of first body = m1 = 90 kg, mass of second body = m2 = 90 kg, Distance between masses = r = 40 cm = 40 x 10-2 m, G = 6.67 x 10-11 N m2/kg2 .
To Find: Force of attraction = F =?
By Newton’s law of gravitation
Even if the same bodies are placed on the Moon, the gravitational force between them remains unchanged because their masses and the distance between them stay the same. This is due to the fact that gravitational force between two objects is independent of any third body or the medium separating them.
Thus, the force of attraction between two metal spheres is 3.377 x 10-6 N.
Example 4: Three 5 kg masses are kept at the vertices of an equilateral triangle each side of 0.25 m. Find the resultant gravitational force on any one mass. G = 6.67 x 10-11 S.I. units.
Solution: m1 = 5 kg, m2 = 5 kg, m3 = 5 kg, r = 0.25 m, G = 6.67 x 10-11 N m2/kg2.
To find: Force on m1 =?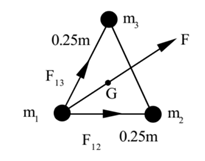 By Newton’s law of gravitation, the force on mass m1 due to mass m2.
By Newton’s law of gravitation, the force on mass m1 due to mass m2.
By Newton’s law of gravitation, the force on mass m1 due to mass m3.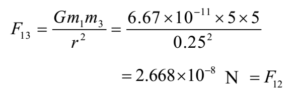 The angle between F12 and F13 is 60°. (Angle of an equilateral triangle). The net force on m1 is given by
The angle between F12 and F13 is 60°. (Angle of an equilateral triangle). The net force on m1 is given by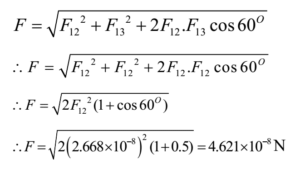 The two forces are equal, hence their resultant act along angle bisector towards centroid.
The two forces are equal, hence their resultant act along angle bisector towards centroid.
The force on any mass is 4.621 × 10⁻⁸ N directed towards the centroid.
Example 5: Two bodies of masses 5 kg and 6 x 1024 kg are placed with their centres 6.4 x 106 m apart. Calculate the gravitational force of attraction between the two masses. Also, find the initial acceleration of two masses assuming no other forces act on them.
Solution: Mass of first body = m1 = 5 kg, mass of second body = m2 = 6 x 1024 kg, Distance between masses = r = 6.4 x 106 m, G = 6.67 x 10-11 N m2/kg2 .
To Find: Force of attraction between two masses = F =? , Initial accelerations of the two masses =?
Ans:
By Newton’s law of gravitation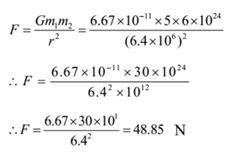
Initial acceleration of the body of mass 5 kg
By Newton’s second law of motion, F = ma
Thus a = F/m = 48.85 / 5 = 9.77 m/s2
Initial acceleration of the body of mass 6 x 1024 kg
By Newton’s second law of motion,
F = ma
Thus 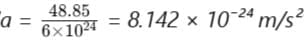
The force of attraction between the two masses = 48.85 N
Mass and Weight
In Newton’s law of gravity, mass plays a crucial role in determining the gravitational force. We often consider mass and weight to be the same, but while they are related, they are different.

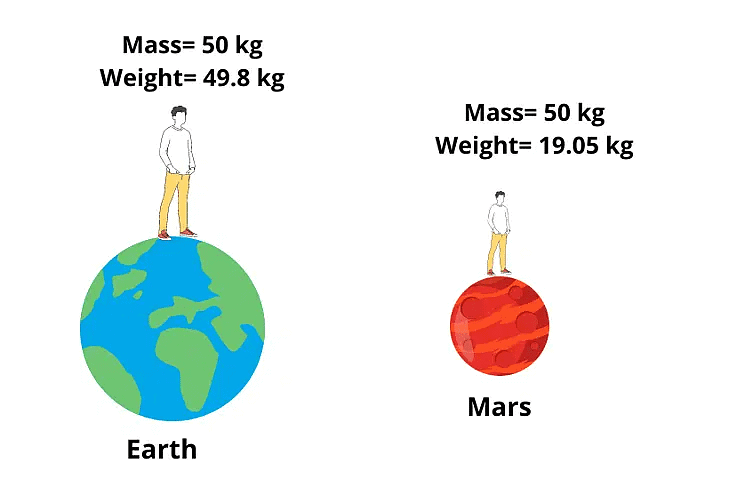 Difference between Mass and Weight
Difference between Mass and Weight
Universality of Gravity
- Gravitational interactions not only exist between the earth and other objects, but they also exist between all objects with an intensity that is directly proportional to the product of their masses.
- The law of universal gravitation helps scientists study planetary orbits. The small perturbations in a planet’s elliptical motion can be easily explained owing to the fact that all objects exert gravitational influences on each other.
Why doesn’t the Moon fall into the Earth?
The forces of speed and gravity are what keeps the moon in constant orbit around the Earth. The Moon seems to hover around in the sky, unaffected by gravity. However, the reason the Moon stays in orbit is precisely because of gravity.
Is the force of Gravity the same all over the Earth?
Gravity isn’t the same everywhere on earth. Gravity is slightly stronger over the places with more underground mass than places with less mass. NASA uses two spacecraft to measure the variation in the Earth’s gravity. These spacecraft are a part of the Gravity Recovery and Climate Experiment (GRACE) mission.
Satellite data shows gravity varies across the Earth’s surface. Blue areas indicate weaker gravity, while red areas represent stronger gravitational pull.
|
96 videos|367 docs|98 tests
|
FAQs on Universal Law of Gravitation - Physics Class 11 - NEET
| 1. What is Newton's Law of Universal Gravitation? |  |
| 2. What are the properties of gravitational force? |  |
| 3. What is the gravitational equation in vector form? |  |
| 4. What is the difference between mass and weight? |  |
| 5. Is the force of gravity the same all over the Earth? |  |





















