VBT, CFT & LFT Theories - 2 | Chemistry Optional Notes for UPSC PDF Download
Ligand Field Theory
- Ligand field theory is the most powerful bonding theory for coordination compounds. It is essentially molecular orbital theory applied to coordination compounds. It can explain covalent bonding in coordination compounds, it can explain their shapes, it can explain their magnetism, and their electronic spectra. It can also explain the stability of coordination compounds, in particular the 18e rule and their exceptions. It is, however, more complicated than other bonding theories.
- Just like in molecular orbital theory we can apply symmetry adapted linear combination of atomic orbitals to construct molecular orbitals. However, slightly modified rules apply to optimize molecular orbital theory for coordination compounds. These modifications are useful due to the greater complexity of coordination compounds. In the first step we determine the point group of the molecule and assign axes in a useful way. In the second step, we determine the valence orbitals, also called frontier orbitals of the metal. For example, for a transition metal of the 4th period we would consider the 4s, the 4p, and the 3d orbitals as the frontier orbitals.
- Next, we determine the symmetry of these orbitals. We can do this by just looking into the character table of the respective point group. In the following we select the highest-energy ligand orbitals that are suitable for σ-bonding. For ligands that are molecules or polyatomic ions, these orbitals are the HOMOs suitable for σ-bonding. For simple ions like chloro-ligands these are the highest occupied atomic orbitals. Next, we group the selected ligand orbitals to form ligand group orbitals (LGOs), and determine their symmetry types. To do so, we determine the reducible representation, and then the irreducible representations of the LGOs. This gives us the symmetry types of the ligand group orbitals. We then combine metal frontier orbitals and ligand group orbitals of the same symmetry type to form molecular orbitals. Now we have constructed all molecular orbitals suitable for σ-bonding, and can draw a molecular orbital diagram for the σ-bonding in the coordination compound.
- Next, we look for ligand orbitals that are suitable for π-bonding with the metal. We then determine the symmetry types of their ligand group orbitals. Ligand group orbitals and metal orbitals of the same symmetry will then be combined to form molecular orbitals. These MOs represent the π-bonding in the molecule. We add these molecular orbitals to the molecular orbital diagram. Finally, we check if there are ligand orbitals suitable for δ-bonding with the metal. If so, we also form ligands group orbitals for these, determine their symmetry types, and combine ligand group orbitals and metal orbitals of the same symmetry to form molecular orbitals. These orbitals will then also be added to the molecular orbital diagram.
Applicable rules for the construction of molecular orbital diagrams using ligand field theory
- Determine point group of the complex and assign axes.
- Determine which are the relevant metal frontier orbitals for bonding.
- Determine symmetry types of these metal orbitals.
- Select ligand HOMOs (suitable for σ-bonding) if the ligand is a molecule. If a simple ion, select the highest occupied atomic orbital.
- Form ligand group orbitals (LGOs) from selected ligand orbitals and determine their symmetry types.
- Combine metal orbitals and ligand group orbitals of appropriate symmetries to form molecular orbitals.
- Select ligand orbitals for π and σ bonding if applicable, determine their symmetry and combine them with appropriate metal orbitals.
Ligand Field Theory for an Octahedral Complex of a 4th Period Transition Metal
- Let us apply the ligand field theory to a 4th period octahedral transition metal complex first. According to the rules we must first determine the point group and define the coordinate system. The point group is obviously Oh.

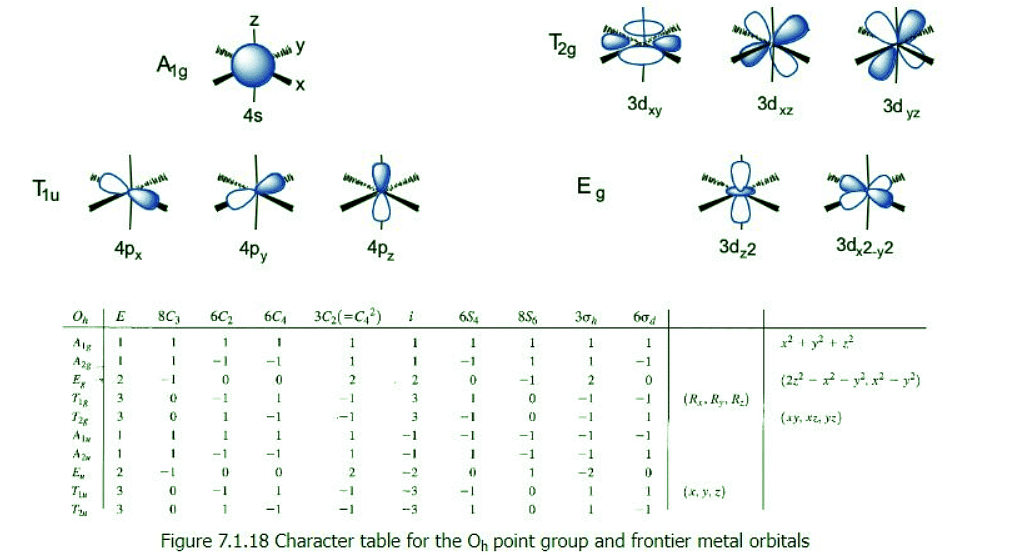
- We can define the coordinate system so that the ligands approach on the x, y, and z axes, respectively. Next, we need to see what the frontier orbitals are. These would be the 4s, the 4p, and the 3d orbitals (Fig. 7.1.18). What symmetry types do they have? We can see this by looking into the character table for the point group Oh. An s orbital always has the totally symmetric symmetry type which is always listed first in the character table. In the point group Oh this is the symmetry type A1g. What about the 4p orbitals? We can see that the letters x,y, and z are in parentheses in the irreducible representation of the symmetry type T1u.
- This means that the three 4p orbitals are triply degenerate and have the symmetry type T1u. Finally, we need to determine the symmetry types of the 3d orbitals. We find xy, xz, and yz in parentheses in the irreducible representation of the symmetry type T2g. Thus, these orbitals have the symmetry type T2g. We further find 2z2-x2-y2 and x2-y2 in the line for the symmetry type Eg , thus the dz2 and the dx2-y2 orbitals are degenerate and have the symmetry type Eg. Remember here from the chapter about atomic structure that 2z2-x2-y2 mathematically describes a cone, and that the dz2 orbital has a conical node. We have now found all the symmetry types of the frontier orbitals.
- Next, we need to direct our attention to the ligand and find the highest occupied molecular or atomic orbital suitable for σ-bonding. Of course, it depends now what the ligand is.

- As an example let us choose the common and interesting carbonyl ligand (Fig. 7.1.19). To determine its HOMO suitable for σ-bonding with the metal, we will first need to know the molecular orbital diagram for the carbon monoxide molecule. The carbon monoxide molecule is a linear, polar molecule that belongs to the point group C∞v.

- The character table of this point group is somewhat hard to work with because of the infinite order of the principal axis, and the infinite number of vertical mirror planes. We will therefore use the subgroup C4v instead (Fig. 7.1.20). A subgroup of a group is a group that results when we remove certain symmetry elements from the original group. We should remove symmetry elements so that degeneracies in the molecular orbitals are not overlooked, which can happen when you reduce the symmetry too much. The point group C4v is the point group with the lowest symmetry we can choose without overlooking degeneracies. Essentially, this is because the atomic orbitals of C and O are only 2s and 2p, and the 2p-orbitals perpendicular to the C-O bond axis can be rotated by 90° to make the orbitals interconvert. This requires a rotational axis of the order 4. If we chose the point group C2v, which has even lower symmetry, we would still be able to construct a molecular orbital diagram, but we would overlook that the 2px and the 2py orbitals are degenerate. We see that in the case of a diatomic linear molecule there is no central atom and no ligands. Therefore, we cannot apply the SALC method exactly as we previously learned it. Therefore, we treat the C and O atoms like central atom orbitals that interact with each other. To determine their symmetry types we can just look into the character table for C4v. We find that the 2s orbitals and the 2pz orbitals have the symmetry type A1 and the 2px and the 2py orbitals are double-degenerate and have the symmetry type E (Fig. 7.1.20). Now we can just combine the atomic orbitals to form molecular orbitals.

- To construct a molecular orbital diagram we must consider that O is considerably more electronegative than C, and therefore, the 2s orbital of O is lower in energy compared to the 2s orbital of C. The 2p orbitals of O are lower in energy than those of C. Now we can label our orbitals with their symmetry types, and combine orbitals of the same symmetry type to form molecular orbitals (Fig. 7.1.21). We can start, for instance, with the orbitals of the A1 symmetry type. There are two on each side, so we will have overall four. Our qualitative assumption would be that there should be a strongly bonding and a strongly anti-bonding orbital, and weakly bonding and a weakly anti-bonding orbital in addition. The strongly bonding one would have the lowest energy and be labeled 1a1, the weakly bonding one would have higher energy and is labeled 2a1, the weakly anti-bonding one has an even higher energy and is labeled 3a1, and the strongly anti-bonding one would have the highest energy of all the four, and has the label 4a1. The strongly anti-bonding orbital must be above the 2pz orbital of C, and the strongly bonding one must be below the 2s orbital of O.
- We can write the 2a1 and the 3a1 orbital at energy levels so that the energy differences between all four a1 orbitals are about the same. We can now also connect the MOs and AOs of a1 symmetry with dotted lines. Now we can turn our attention to the orbitals with E symmetry. There are overall four orbitals of E symmetry, therefore, we expect two bonding double–degenerate orbitals with e-symmetry, and two anti-bonding double-degenerate orbitals with e-symmetry. The bonding MOs must be below the energy level of the 2p orbitals of O, and the two anti-bonding orbitals must be written above the energy levels of the 2p orbitals of C. We can now connect the atomic and molecular orbitals with dotted lines. Finally, we still need to fill in the electrons. There are four electrons coming from the carbon and six electrons coming from the oxygen, which gives ten electrons overall. This means that the 1a1, the 2a1, the 1e1 and the 3a1 molecular orbitals are full. This makes the 3a1 orbital the HOMO. It is suitable for σ-bonding with the metal because it has been created through σ-interactions between the 2pz and the 2s orbitals of O and P respectively.
- It is again interesting to compare the MO picture of the bonding in CO with the Lewis-dot structure (Fig. 7.1.19). In the Lewis dot structure we have a triple bond with six bonding electrons. They correspond to the bonding 1a1 and 1e electrons. In the Lewis dot structure all six electrons are energetically indistinguishable, but in the MO diagram we can clearly see that two electrons have a lower energy than the other four which are energetically degenerate. The 1a1 MO is a σ-orbital while the other two are π-orbitals because the 2px and the 2py orbitals interaction in π-fashion. The 2a1 and 3a1 orbitals can be approximated as non-bonding MOs representing the two electron lone pairs at C and O respectively. Because the 3a1 is slightly anti-bonding it has its electron density mostly at C, while the 2a1 is slightly bonding and therefore its counterpart is the electron lone pair at O. Interestingly the dipole moment of CO is slightly polarized toward C by 0.1 Debye despite the fact that O is the more electronegative atom. This can be attributed to the fact that the HOMO as a weakly anti-bonding orbital is primarily located at C, In addition, the 2a1 orbital is fairly close in energy to the 2s of C, therefore the 2s of C contributes significantly to this orbital. This leads to the fact that there is a significant amount of electron density located at C as well.

- In the next step, we need to group the six HOMOs to form ligand group orbitals, and determine their symmetry types. This is being done by first determining the reducible representation of the orbitals using the orbital swapping method, and then determining the number of irreducible representations of a given type using the reduction formula from group theory. We will not go through the details of the calculations here, because there is nothing really new to learn, but just discuss the outcome.
- The outcome is that there is one ligand group orbital with the symmetry type a1g, two doubly degenerated ligand group orbitals with the symmetry type eg, and three triply degenerated ligand group orbitals having the symmetry type t1u. The a1g orbital does not have a node because it is totally symmetric. The t1u orbitals have one node, and the eg-orbitals have two nodes (Fig. 7.1.22). This is not a result of the reduction formula, but one could show that by actually computing the ligand group orbitals using a formula called the projection operator (which we will not discuss in detail here).
- Because we now know our the symmetry types of our metal frontier orbitals and our ligand group orbitals we can construct a qualitative molecular orbital diagram (Fig. 7.1.23). To do so we can plot the frontier orbitals on the left side of the molecular orbital diagram, and the ligand group orbitals on the right side of the molecular orbital diagram.

- For a 4th row transition metal the sequence of energy is 3d<4s<4p. It makes sense to assume that the ligand group orbitals have about the same energy as the 3d orbitals of the metal, and we can plot them accordingly. Next, we can assign the orbitals their previously determined symmetry types. Then, we can start to combine orbitals of the same symmetry types to form molecular orbitals. We can start for instance with the orbitals having the symmetry type A1. The 4s orbital has that symmetry type. Also one ligand group orbital is of this type. Therefore, we would expect one bonding and one anti-bonding molecular orbital. We can label them 1a1g and 2a1g, respectively, and connect them with the A1g atomic and ligand group orbitals by dotted lines. Next, for example, we can consider the Eg orbitals. There are two metal d orbitals and two ligand group orbitals of that symmetry. We therefore produce two doubly degenerate bonding, and two doubly degenerate anti-bonding molecular orbitals. We can label them 1eg and 2eg respectively. We can further see, that there are the three T1u metal 4p orbitals that we can combine with the ligand T1u orbitals. This gives three triple-degenerated bonding orbitals and three triple-degenerated anti-bonding orbitals with t1u symmetry. Lastly, there are the metal T2g orbitals. There are no ligand group orbitals with the same symmetry, and therefore the T2g orbitals remain non-bonding. We have to write them with unchanged energy into the molecular orbital diagram.
- Now we are finished with the construction of molecular orbitals, but still need to fill the electrons into them. We consider the metal-ligand bond a dative bond, with electron pairs being donated by the ligand’s HOMO. Therefore, we consider all ligand group orbitals to be full with electrons. That means that we have overall 6 x 2 = 12 electrons to consider. What about the metal electrons? Well, it depends now which metal ion we have. Let us assume here that we have a d0 metal ion with no d electrons. That means that we overall have 12 electrons that we need to fill into the molecular orbitals according to energy. This fills the 1a1g, three t1u, and the two 1eg orbitals. Now let us assume that we would not have a d0 metal ion, but a metal ion with d electrons. There could be up to ten d electrons. Where would they go? They would go into the five orbitals with the next highest energies. Which ones are these? Well, these are the t2g and the 2eg orbitals. The t2g orbitals are the non-bonding metal dxz, dxy, and dyz orbitals, therefore these orbitals are located only at the metal. The 2eg orbitals are anti-bonding molecular orbitals that have been constructed from the dz2 and the dx2-y2 orbitals, and are similar in energy to the dx2-y2 and dz2 orbitals. We can therefore say that the t2g and the 2eg orbitals are the d orbitals under the influence of an octahedral ligand field. Due to the presence of the ligand field the energies of the metal d-orbitals split and the difference in energy is the octahedral ligand field energy Δo. Now we can see that there is an interesting analogy to the crystal field theory. Like the d-orbitals split in energy under an octahedral crystal field into t2g and eg orbitals, the d-orbitals split in energy in an octahedral ligand field into t2g and eg orbitals. Like in crystal field theory the energy of the dz2 and the dx2-y2 is raised. The energy of the other three d-orbitals is unaffected similar, but not exactly the same as the dxy, dyz, and the dxz orbitals in an octahedral crystal field.

- Now we have understood the σ-bonding in an octahedral complex, next let us consider the π-bonding. That means that we have to think about what orbitals of the ligand has the right symmetry for π-bonding with the metal. They should also have an energy similar to the metal orbitals so that significant covalent interaction can occur. We shall stick with our carbonyl ligand, thus we need to look into the molecular orbital diagram of the CO molecule again, and see if there are molecular orbitals suitable for π-bonding (Fig. 7.1.24). The CO molecule has the 1e and the 2e orbitals, that are bonding and anti-bonding π-orbitals, respectively. We can understand this when considering that they are constructed from the 2px and the 2py orbitals that overlap in π-fashion to make the π-bonding in the molecule. Each ligand has two 1e and two 2e orbitals which gives overall four orbitals. These orbitals are energetically similar to the HOMO, thus we can expect that they are energetically close enough to the energy of d-metal orbitals, and can get involved in bonding. We have six ligands meaning that we have 6x12=24 orbitals overall. The twelve 1e orbitals are bonding π-orbitals, and the twelve 2e orbitals are anti-bonding π*-orbitals.
- Why are these orbitals suitable for π-bonding with metal d-orbitals? Let us look at their shape, and how they can overlap with a metal d-orbital (7.1.25).

- Look for example at a 1e orbital constructed from two 2px orbitals, and how it is oriented relative to the metal-ligand bond axis which we shall define as the z-axis. Next, let us consider a metal dxz orbital orbital. We can see that it is in plane with the 1e orbital, and that the overlap between the dxz and the 1e orbital occurs in π-fashion. Now let us consider the analogous π*-orbital. We can see that it has an additional node, but it can also overlap with a dxz orbital in π-fashion. The ligand does not only have π and π*-orbitals through overlap of two 2px orbitals, but also π and π*-orbitals that result from the overlap of two 2py orbitals. Those orbitals can overlap in π-fashion with a metal dyz orbital. So far, we considered the interactions of a single ligand with the metal only. There are five other ligands, one also approaching from the z-axis, and the other four approaching from the x and y axes. They also have the π and π*-orbitals that interact with the dxz, the dyz, or the dxy orbitals in π-fashion, depending on the direction of approach.
- So what do we do with all these orbitals? We group the twelve bonding ones to form a set of ligand group orbitals, and group the twelve anti-bonding ones to form another set of ligand group orbitals. We determine the symmetry types of each set by first determining the reducible representation, and then the irreducible representations using the reduction formula. The result of this process is that the twelve bonding ligand group orbitals have T1g, T2g, T1u, and T2u symmetry. This means that there are three triple-degenerated ones that have T1g symmetry, three other triple-degenerated ones that have T1u, symmetry, three more triple-degenerated ones that have T1u symmetry, and another three triple-degenerated ones that have T2u symmetry. The twelve anti-bonding ligand group orbitals have the same symmetry types. Three have T1g symmetry, three have T2g symmetry, three have T1u symmetry, and another three have T2u symmetry.

- It should be mentioned that there are a number of other orbitals that can make π-interactions when the ligand is not a CO ligand. For example halogenide ligands have p-orbitals that have suitable orientation to overlap with metal d-orbitals in π-fashion (Fig. 7.1.26). When there are complexes with metal-metal bonds then there is also the possibility of metal d-orbitals to overlap with other metal d-orbitals in π-fashion.

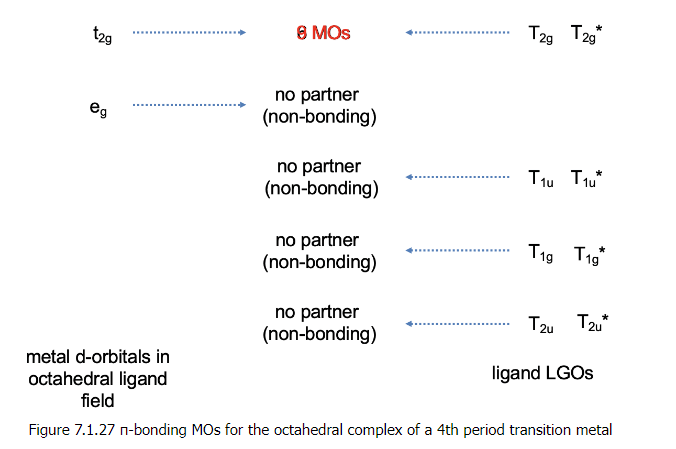
- Now that we have determined the symmetry types of the ligand group orbitals available for π-bonding, we need to select those ligand group orbitals that have suitable symmetry to form molecular orbitals with metal d-orbitals in the octahedral ligand field. These are the 2eg and the t2g MOs that resulted from the σ-interactions. For simplicity sake we will call the 2eg molecular orbitals just the metal eg orbitals. The t2g MOs are identical to the metal T2g atomic orbitals because the metal T2g atomic orbitals remain exactly non-bonding with respect to σ-interactions. The ligand group orbitals have T1g, T2g, T1u, and T2u symmetry respectively. That means that we can combine the t2g metal orbitals and the T2g ligand group orbitals to form molecular orbitals. The metal eg orbitals and the ligand T1g, T1u, and T2u orbitals remain non-bonding because they do not find a partner (Fig. 7.1.27). The three bonding T2g LGOs will form six MOs of the same symmetry type with the three metal t2g orbitals. In addition, we need to consider that there are also three anti-bonding T2g* LGOs that were formed from the anti-bonding π-orbitals. They can also interact with the metal t2g d-orbitals. Because the number of MOs of a given symmetry type is always the sum of the atomic orbitals + the LGOs of that symmetry type this adds three MOs to the six MOs giving overall nine t2g MOs. There are also the T1u*, the T1g*, and the T2u* orbitals. They just remain non-bonding because they do not find a partner.
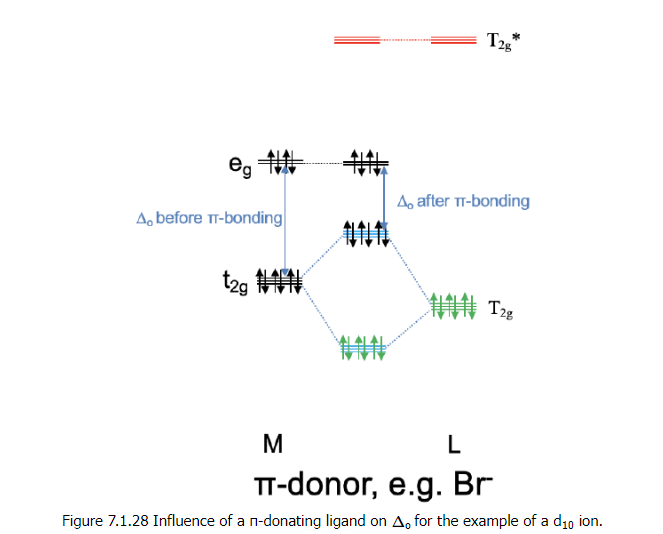
- We can now think of two extreme cases for the combination of the metal t2g with the ligand T2g and T2g* orbitals. In the first case the T2g LGOs are much closer in energy to the metal t2g orbitals, and the T2g* LGOs are energetically much higher than the metal t2g orbitals. In this case we can neglect the covalent interactions between the T2g* orbitals and the metal t2g orbitals, and the T2g* orbitals remain effectively non-bonding. We would consider only the interactions between the T2g LGOs and the metal t2g orbitals to form three bonding and three anti-bonding MOs of t2g symmetry (Fig. 7.1.28). Now we need to consider the electrons. The bonding T2g LGOs are full, and therefore there are overall six electrons to consider. These six electrons would go into the three bonding t2g MOs. Now can also have up to ten metal d electrons. Six of them can be accommodated by the t2g metal orbitals, the other four would be in the eg orbitals. Upon the formation of the π-bond, the t2g metal electrons will be in the anti-bonding t2g orbitals. The eg electrons will simply remain non-bonding. We can see that the π-interactions lower the energy of the ligand electrons, but increase the energy of the metal electrons. If we get a net stabilization of electron energies will depend on how many d electrons we have. As long as there are less than six d electrons we will see a stabilization, if there are more there will be an overall destabilization. We can also ask what impact the π-bonding has on the magnitude of the Δo. We can see that the π-bonding decreases the Δo. It is larger before the bonding compared to after the π-bonding.

- We call a ligand that has T2g orbitals of similar energy to the metal t2g orbitals, and T2g* orbitals of much higher energy compared to the metal t2g orbitals a π-donating ligand, or a π-donor (Fig. 7.1.28). This is because before the π-bonding the ligand electrons are localized exclusively at the ligand, and after the π-bonding they are in the bonding t2g MOs which are shared between the metal and the ligand. Thus, a partial electron transfer has occurred from the ligand to the metal. An example for π-donating ligands are halogenide ligands such as a bromo ligand.

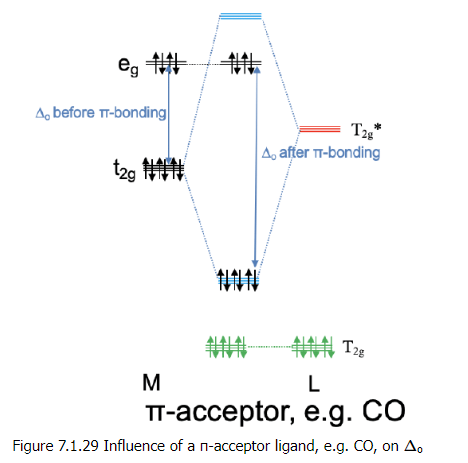
- Now let us consider the opposite case in which the anti-bonding T2g* ligand orbitals are energetically close to the metal t2g orbitals and the bonding T2g ligand orbitals are energetically too low in order to significantly interact with the metal t2g orbitals. This means that the T2g-orbitals remain practically non-bonding. The T2g* ligand group orbitals and the metal t2g orbitals form three triply degenerated bonding molecular orbitals and three triply degenerated anti-bonding molecular orbitals. Because the T2g* ligand group orbitals are empty, no ligand electrons are filled into the new molecular orbitals. This means that up to six metal d electrons can be filled into the bonding molecular orbitals of t2g symmetry. Any remaining d electrons in the eg orbitals just remain in the eg orbitals and do not change in energy. We can see that in contrast to the previous case, we can lower the energy of the metal d electrons through π-interactions. Because the bonding t2g electrons are shared between the metal and the ligand, electron density has been transferred from the metal to the ligand. Therefore, a ligand that primarily utilizes its anti-bonding T2g*-orbitals for π-bonding is called a π-acceptor ligand, it accepts d-electron density from the metal. An example for a π-acceptor ligand is the carbonyl ligand (Fig. 7.1.29). It is also important to understand the influence of a π-acceptor ligand on the size of Δo. Because the anti-bonding t2g MO is higher in energy than the non-bonding eg orbitals, the Δo is now defined by the energy difference between the bonding t2g MOs and the eg orbitals (Fig. 7.1.29). We can see that Δo is increased when π-acceptor interactions are taken into account.
- We have now discussed the two extreme cases, however there are many ligands that are actually in between these two extremes, and there is a continuous spectrum from strongly π-donating, to weakly π-donating, to weakly π-accepting, to strongly π-accepting ligands. It is also possible that π-donor and π-acceptor effects cancel out. This is the case when the the T2g and T2g*-ligand group orbitals are energetically about equidistant to the metal t2g orbitals. Some ligands also do not have orbitals suitable for π-bonding at all, and there are neither π-donating nor π-accepting effects.
- The effect of π-bonding on Δo can nicely explain the spectrochemical series. Because π-accepting ligands increase Δo, these complexes absorb light of shorter wavelength and of higher energy. π-donating ligands decrease Δo and and thus lead to the absorption of light having longer wavelengths. We see here that the ligand field theory is more powerful than the crystal field theory. The latter was not able to explain why different ligands produce different Δo values.
- Ligand field theory is also able to nicely explain the magnetism of coordination compounds, and high and low spin complexes in particular. It is also able to explain why certain ligands tend to produce low spin complexes, while others tend to form high spin complexes. According to ligand field theory π-acceptors tend to make low spin complexes, and π-donors tend to make high-spin complexes. This is in accordance with experimental observation.
Octahedral Complexes and The 18 Electron Rule
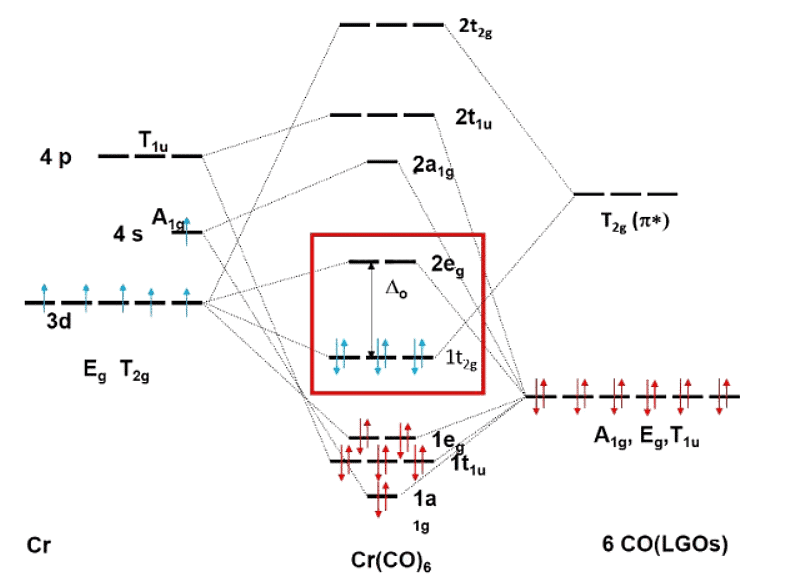
Figure 7.1.30 Qualitative MO diagram of the octahedral hexacarbonyl chromium complex under consideration of π -bonding.
Another great feature of ligand field theory is that it can explain the 18 electron rule, and exceptions from the 18 electron rule. For example, the octahedral hexacarbonyl chromium complex is an 18 electron complex. Let is construct a qualitative molecular orbital diagram and see if the MO diagram supports the stability of the complex. The MO diagram considering only the σ-interactions is shown in Fig. 7.1.30. We can see that all the twlelve ligand electrons are in the bonding molecular orbitals 1a1, 1tu, and 1eg. In addition the chromium has six valence electrons. These electrons remain non-bonding when considering σ-interactions only. However, this changes, when we consider π-interactions. The CO ligand is a strong π-acceptor ligand, therefore we consider only its T2g* π-ligand group orbitals for bonding. They must be located energetically above the LGOs for σ-bonding. The interaction of the metal t2g orbitals creates three bonding t2g MOs and the three anti-bonding ones. Because we can fill metal d electrons into the bonding MOs the status of the d-electrons has changed from non-bonding to bonding. We can see now that all 18 electrons are in bonding MOs, and that no electron is in-non-bonding or anti-bonding MOs. When all electrons are in bonding MOs then this is the ideal situation for complex stability. This is explains why the 18 electron complex is stable. If we analyzed the MO diagrams of many other stable 18 electron complexes then we would also mostly find that all bonding MOs are filled, and all other MOs are empty. This explains the 18 electron rule.
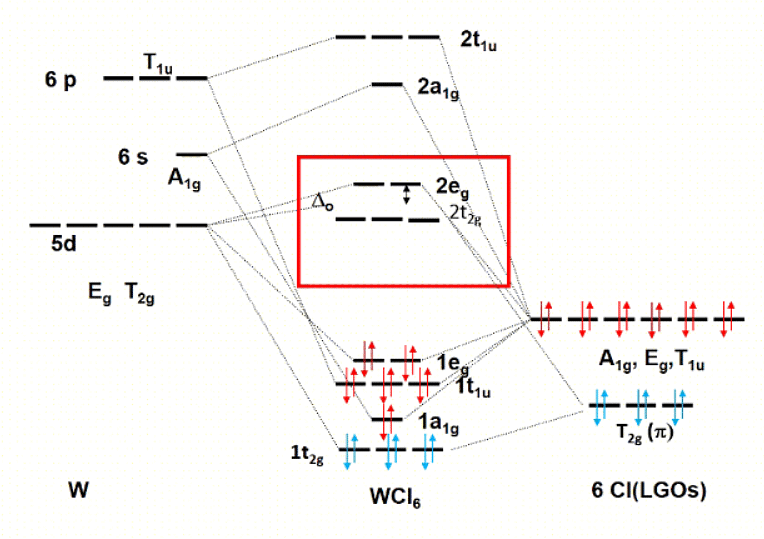
Figure 7.1.31 The qualitative molecular orbital diagram of WCl6 under consideration of π -bonding.
Next, let us construct a qualitative molecular orbital diagram of WCl6. This is not an 18 electron complex, it has only twelve electrons coming from the six chloro ligands. W is in the oxidation state +6 and is a d0 species contributing no electons. Can ligand field theory explain this exception from the 18 electron rule? Let us again start with the MO diagram considering σ-bonding only. The twelve ligand electrons go into the bonding 1a1g, 1tu, and 1eg orbitals. The non-bonding t2g and the anti-bonding 2eg orbitals remain empty due to the absence of metal d electrons. We can see that all bonding molecular orbitals are full and all others are empty, explaining the stability of the molecule, and thus the exception from the 18 electron rule. Now let us consider π-bonding in addition. A chloro ligand is a typical π-donor which uses its 3p electrons that are suitably oriented for π-bonding. Therefore, we only consider the T1g ligand group orbitals for bonding here. These orbitals are full with electrons because a chloride anion has a full 3p subshell. The interaction of the T2g LGOs with the metal t2g orbitals creates a bonding t2g MO and an anti-bonding t2g MO. We can see that the ligand π-electrons now have a lower energy than without the π-interactions of the metal. Therefore, the π-bonding has further stabilized the complex. In a way, we can now even say that we have an 18 electron complex because when we add th 6 π electrons to the 12 σ electrons we get 18 bonding electrons overall. These additional 6 electrons are not accounted for in electron-counting because electron-counting treats the W-Cl bond as a single bond and only considers the σ-interactions between W and Cl.
FAQs on VBT, CFT & LFT Theories - 2 - Chemistry Optional Notes for UPSC
| 1. What is Ligand Field Theory? |  |
| 2. What is the significance of an octahedral complex in Ligand Field Theory? |  |
| 3. What is the 18 Electron Rule in Ligand Field Theory? |  |
| 4. How does Ligand Field Theory relate to Valence Bond Theory (VBT) and Crystal Field Theory (CFT)? |  |
| 5. How does Ligand Field Theory explain the colors observed in transition metal complexes? |  |

|
Explore Courses for UPSC exam
|

|