Vapour Pressure of Liquid Solutions: Raoult’s Law | Chemistry Class 12 - NEET PDF Download
What is Vapour Pressure?
A liquid solution is created by dissolving a solid, liquid, or gas in a specific liquid solvent. The Vapour Pressure of liquid solutions is defined as the pressure exerted by the vapours on the liquid solvent when the system reaches equilibrium at a particular temperature.
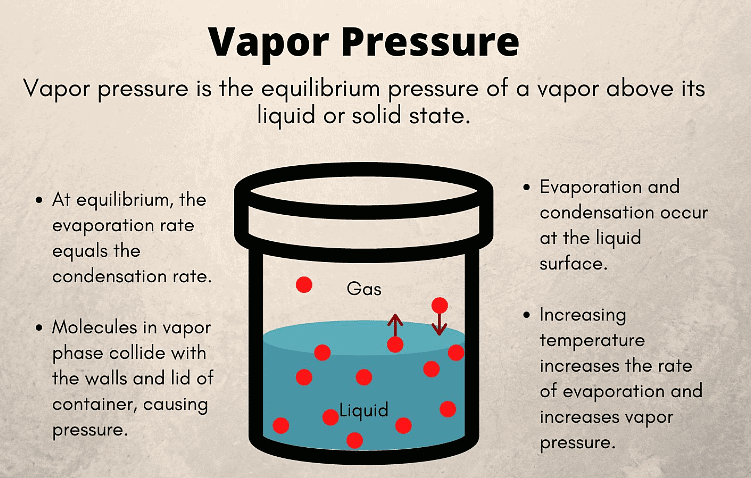
This pressure varies depending on the nature of the liquid and the ambient temperature.
Several characteristics of the vapour pressure of liquid solutions can be identified:
Characterstics of Vapour Pressure
1. The vapour pressure of a pure liquid is higher compared to that of a liquid solution. For instance, if you take two beakers—one filled with water and the other with a mixture of lemon juice and water—you will observe that the beaker with pure water exhibits higher vapour pressure.
2. Vapour pressure is inversely proportional to the forces of attraction between molecules in a liquid.
3. Vapour pressure increases with rising temperature, as molecules acquire more kinetic energy and undergo more rapid vaporization.
 Liquid solutions may consist of both volatile solutes and solvents. Typically, the solvent is volatile, while the solute remains non-volatile. The evaluation of vapour pressure can occur in two scenarios:
Liquid solutions may consist of both volatile solutes and solvents. Typically, the solvent is volatile, while the solute remains non-volatile. The evaluation of vapour pressure can occur in two scenarios:
1. Vapour Pressure of Liquid-Liquid Solutions: Both solute and solvent are in the liquid phase.
2. Vapour Pressure of Solid-Liquid Solutions: The solute is in a solid state, and the solvent is in the liquid phase.
Vapour Pressure of Liquid-Liquid Solutions
Determining the vapour pressure of a liquid-liquid solution involves the utilization of two volatile liquid solutions, denoted as A and B for their liquid components. Placing these volatile liquids and their respective components within a sealed container results in the establishment of equilibrium between the liquid and vapour phases.
- Assuming P total signifies the comprehensive vapour pressure in the equilibrium state, and denoting PA and PB as the partial vapour pressures attributed to components A and B respectively. Additionally, introducing the mole fraction of the respective components as xA and xB.
- In the assessment of the vapour pressure of volatile liquids in this context, Raoult’s Law serves as the guiding principle.
Raoult’s Law
The law states that the partial pressure is directly proportional to the mole fraction of the solute component.
So, according to Raoult’s Law, the partial pressure of A will bePA ∝ xA
PA = PA0 xA
where PA0 is the vapour pressure of pure liquid component A. Similarly partial pressure of B will be
PB ∝ xBPB = PB0 xB
where PB0 is the vapour pressure of pure liquid component B.
Now, by Dalton’s law of partial pressures, this states that total pressure ( Ptotal) the solution placed in a container is the sum of partial pressures of its respective components. That is
Example: Calculate the relative lowering of vapour pressure when 12 g urea (Mol weight 60 g/mol) is dissolved in 90 g of water.
Solution:
Relative lowering of vapour pressure is given by :
ΔP /PoA = nB/(nA + nB)
nB=Moles of urea
nA=Moles of water
nB=1260=0.2; nA=9018=5
△p/p0 = 0.2/(0.25+0.2) = 0.038
Example: If vapour pressure of pure liquid A is 100 mm Hg and Vapour pressure of pure liquid B is150 mm Hg. 2 mole of liquid A and 3 mole of liquid B are mixed to form an ideal solution. What is the vapour pressure of solution?
Solution: 130 mm
Vaour pressure of pure B, (p∘B) = 150 mm Hg
2 mol of liquid 'A' and 3 mol of liquid 'B' are mixed to form an ideal solution. The vapour pressure of solution will be:
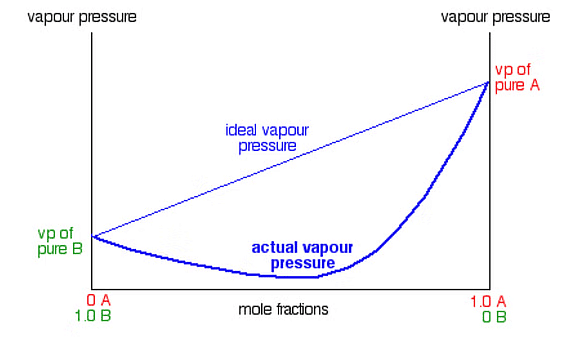
Conclusions on Vapour Pressure Relation in liquid-liquid Solutions
Following conclusions are observed from the following relation.
- Total vapour pressure relies on mole fraction of any one of the component that is, either A or B. For Example, the equation can also be written as
Ptotal = PB0 + (PA0 – PB0) XA - We can draw a linear graph between total pressure and mole fraction of any of the following component
- Total vapour pressure increases or decreases with respect to mole fraction of component A, depending on pure vapour pressures of components A and B
- If the components are in vapour form, the total vapour pressure can be calculated as
PA = yA Ptotal
PB = yB Ptotal
where yA and yB are mole fraction of components A and B in the vapour phase.
Example: The vapour pressures of pure chloroform CHCl3 and dichloromethane CH2Cl2 are 200 mm Hg and 415 mm Hg. If we add 30 g of CHCl3 and 42 g of CH2Cl2 at some normal temperature 298 K, then what will be the total vapour pressure of solution? Also, find out mole fraction of both the components in the vapour phase.
Solution:
So, in this problem, we have two liquid solutions chloroform CHCl3 and dichloromethane CH2Cl2. To find out total vapour pressure, we need mole fraction of both the components.
We know that mole fraction of component A = moles of A / Total moles of the solution
And moles of component is mass of component/ molar mass of component
Moles of chloroform CHCl3 = 30/ 119.5 = 0.25
Moles of dichloromethane CH2Cl2 = 42/ 85 = 0.49
Let A component be CHCl3 and B component be CH2Cl2 , then
xA = 0.25 / ( 0.25 + 0.49) = 0.25 / 0.74 = 0.33
xB = 0.49 / ( 0.25 + 0.49) = 0.49 / 0.74 = 0.66
Also, we have PA0 as 200 mm Hg and PB0 as 415 mm Hg
Then total vapour pressure P equals, Ptotal = PA0 xA + PB0 xB
Ptotal = 200 × 0.33 + 415 × 0.66 = 339.9 mm Hg
Let the mole fraction of CHCl3 chloroform yA and CH2Cl2 be yB in vapour phase, then we know that
PA = YA Ptotal
PA0 XA = YA Ptotal
200 × 0.33 =YA Ptotal
66 / 339.9 = YA
0.19 = YA
Also, YA + YB = 1
Then YB = 1 – YA = 1 – 0.19 = 0.81
So, the total vapour pressure of the solution is 339.3 mm Hg and mole fraction of CHCl3 chloroform is 0.19 and that of CH2Cl2 dichloromethane is 0.81 respectively.
Vapour Pressure of Solutions of Solids in Liquids
When creating a sugar solution, sugar is introduced into water, where sugar serves as the non-volatile solute, and water functions as the solvent. Upon evaporating this sugar solution, the vapor phase solely comprises vapors of the solvent (water) since the solute is non-volatile. Nevertheless, it is observed that the vapor pressure of this solution is lower than that of the pure solvent (water).
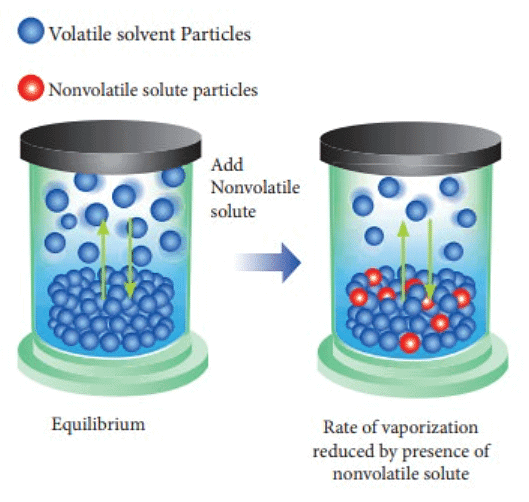
- The vapor pressure of a solution, which includes a non-volatile solute and a solvent, is contingent upon the rate at which solvent molecules escape from the liquid's surface.
- Consequently, the vapor pressure of the solution (sugar + water) is diminished compared to that of the pure solvent (water), indicating a reduction in vapor pressure due to the presence of a non-volatile solute. As the concentration of sugar in the solution rises, the vapor pressure of the solution experiences further reduction.
- The decline in the vapor pressure of the solvent is dependent on the quantity of non-volatile solute within the solution and is not influenced by its nature.
Why Vapour Pressure Decreases when a Non-Volatile Solute is Added to the Solvent?
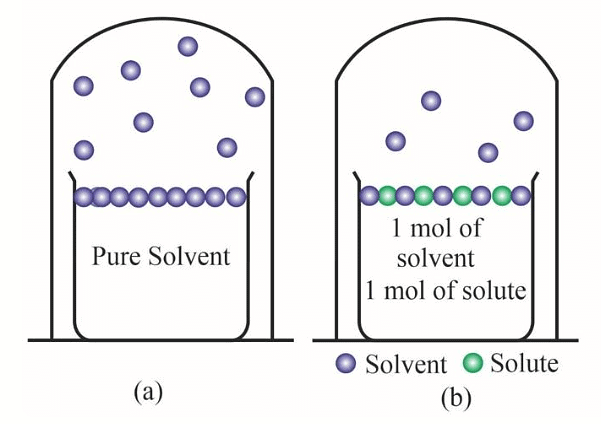 Pure solvent has more number of molecules on the surface (a) as compared to (b) that has a non-volatile solute added to the solution
Pure solvent has more number of molecules on the surface (a) as compared to (b) that has a non-volatile solute added to the solution
The decrease in vapour pressure is due to:
1.Evaporation is a surface phenomenon; hence, the more the surface, the higher the rate of evaporation and the more is the vapour pressure. The non-volatile solute occupies a certain surface area of the entire solution. As a result lesser number of solvent molecules are available on the surface that will escape as vapours.
2. The number of molecules evaporating or leaving the surface is much greater in pure liquid solutions than that of a non-volatile solute solution.
Raoult’s Law of Solutions of Solids in Liquids
To find out overall vapour pressure of the solid-liquid solution, we consider a solution in which lets say A is solvent and B is solute. According to Raoult’s law, we know that partial vapour pressure of individual component (solute/solvent) is directly proportional to its mole fraction.
 Graph between Vapour Pressure and mole fraction in case of solid in liquid solution.Now, when we add a non-volatile solute, it is obvious that vapour pressure will only come from the solvent part, as they are an only available component in the vapour phase. Hence, if PA is the vapour pressure of the solvent, xA is its mole-fraction and PA0 is the vapour pressure of the pure solvent, then by Raoult’s law, the relation will come out to be:
Graph between Vapour Pressure and mole fraction in case of solid in liquid solution.Now, when we add a non-volatile solute, it is obvious that vapour pressure will only come from the solvent part, as they are an only available component in the vapour phase. Hence, if PA is the vapour pressure of the solvent, xA is its mole-fraction and PA0 is the vapour pressure of the pure solvent, then by Raoult’s law, the relation will come out to be:
PA ∝ xA
PA = PA0 xA
When we plot a graph between mole fraction of solvent and vapour pressure, we find its nature to be linear.
|
102 videos|282 docs|123 tests
|
FAQs on Vapour Pressure of Liquid Solutions: Raoult’s Law - Chemistry Class 12 - NEET
| 1. What is Vapour Pressure? |  |
| 2. Why does Vapour Pressure Decrease when a Non-Volatile Solute is Added to the Solvent? |  |
| 3. What is Raoult’s Law and how does it relate to Vapour Pressure in liquid-liquid Solutions? |  |
| 4. How does the Vapour Pressure of Solutions of Solids in Liquids differ from that of liquid-liquid solutions? |  |
| 5. What are the Conclusions on Vapour Pressure Relation in liquid-liquid Solutions based on Raoult’s Law? |  |

|
Explore Courses for NEET exam
|

|
















