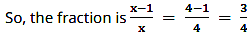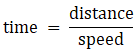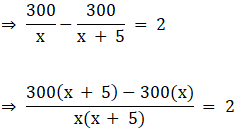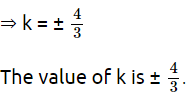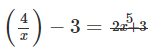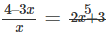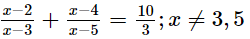Worksheet Question and Solutions: Quadratic Equations Class 10 Worksheet Maths

Q.1. A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.
Ans:
Given, a natural number increased by 12 equals to 160 times its reciprocal.
We have to find the natural number.
Let the natural number be x.
So, x + 12 = 160(1/x)
On transposing 1/x to L.H.S ,we get, x2 + 12x = 160
x2 + 12x - 160 = 0
On factoring,
x2 + 20x - 8x - 160 = 0
x(x + 20) - 8(x + 20) = 0
(x - 8)(x + 20) = 0
Now, x - 8 = 0 x = 8
Also, x + 20 = 0
x = -20
Since a negative number cannot be negative, x = -20 is neglected.
Therefore, the natural number is x = 8.
Q.2. By increasing the list price of a book by ₹ 10, a person can buy 10 books less for ₹ 1200. Find the original list price of the book.
Ans: Let original book price = X
Number of books that can be bought in 1200 =1200/x
Suppose price increases by 10.
New price = x + 10
No of books that can be bought in new price = 1200/(x + 10)
Now, this number is 10 less than the no of books that can be bought in 1200 at ‘x’ price.We are given that, 1200/x−(1200/x+10)=10
⇒1200×10=10x(x+10)
⇒x2+10x−1200=0
⇒x2+40x−30x−1200=0
⇒x(x+40)−30(x+40)=0
⇒(x+40)(x−30)=0
⇒x=−40,30
This is a quadratic equation having two solutions, 30 & -40.
Ignoring negative value the answer is x = 30
So original book price is Rs 30
Q.3. The hypotenuse of a right-angled triangle is 1 cm more than twice the shortest side. If the third side is 2 cm less than the hypotenuse, find the sides of the triangle.
Ans:Let the shortest side of the right triangle be x m
Then,
Hypotenuse = (2x - 1) m
And Third side = (x + 1) m
Using Pythagoras Theorem
Hypotenuse² = (Side 1)² + (Side2)²
(2x - 1)² = x² + (x + 1)²
4x² - 4x + 1 = x² + x² + 2x + 1
4x² - 4x + 1 = 2x² + 2x + 1
⇒ 4x² - 2x² - 4x - 2x + 1 - 1 = 0
⇒ 2x² - 6x = 0
⇒ 2x (x - 3) = 0
⇒ 2x = 0 or x - 3 = 0
⇒ x = 0 or x = 3
⇒ x = 3
[ By rejecting x = 0 Since , Side cannot be 0 ]
Thus, x = 3
⇒ 2x - 1 = 2(3) - 1 = 5 { Hypotenuse }
⇒ x + 1 = 3 + 1 = 4 { Third side }
Obviously x = 0 cm is not a realistic answer in this case.
The only acceptable answer is x = 8 cm
The two shorter sides are 8, 15 and the hypotenuse is 17 cm.
Q.4. A passenger train takes 2 hours less for a journey of 300 km, if its speed is increased by 5 km/hr from its usual speed. Find its usual speed.
Ans: Given: A train takes two hours less for a journey of 300 km
Formula Used: Distance = Speed × Time
Calculation: Suppose the usual speed of the train = x km/hr
According to the question
300/x – 300/(x + 5) = 2
⇒ 300x + 1500 – 300x = 2x2 + 10x
⇒ 2x2 + 10x – 1500 = 0
⇒ 2x2 + 60x – 50x – 1500 = 0
⇒ 2x (x + 30) – 50(x + 30) = 0
⇒ (x + 30) (2x – 50) = 0
⇒ x = 25 (As negative value of x is not possible)
∴ Usual speed of train is 25 km/hr.
Q.5. The numerator of a fraction is one less than its denominator. If three is added to each of the numerator and denominator, the fraction is increased by 3/28. Find the fraction.
Ans:
Let the denominator = x
Given that numerator is one less than the denominator
⇒ numerator = x – 1
So, the fraction = (x - 1)/x
According to the question,x - 1 + 3x + 3 = x - 1x + 328
⇒ x + 2x + 3 = x - 1x + 328
⇒ x + 2x + 3 − x - 1x = 328
⇒ (x + 2)(x) − (x + 3)(x − 1)(x + 3)(x) = 328
⇒ 28{(x2 + 2x) – (x2 –x + 3x – 3)} = 3 (x2 + 3x)
⇒ 28x2 + 56x – 28x2 – 56x + 84 = 3x2 + 9x
⇒ 3x2 + 9x – 84 = 0
⇒ x2 + 3x – 28 = 0
⇒ x2 + 7x – 4x – 28 = 0
⇒ x(x + 7) – 4(x + 7) = 0
⇒ (x – 4) (x + 7) = 0
⇒ x = 4 and – 7
But x is a natural number
Hence, x = 4
Q.6. The difference of squares of two natural numbers is 45. The square of the smaller number is four times the larger number. Find the numbers
Ans:
Let the smaller natural number be x and larger natural number be y
Hence x2 = 4y → (1)
Given y2 – x2 = 45
⇒ y2 – 4y = 45
⇒ y2 – 4y – 45 = 0
⇒ y2 – 9y + 5y – 45 = 0
⇒ y ( y – 9 ) + 5 ( y – 9 ) = 0
⇒ ( y – 9 ) ( y + 5 ) = 0
⇒ ( y – 9 ) = 0 o r ( y + 5 ) = 0
∴ y = 9 o r y = − 5
But y is natural number, hence y ≠ - 5
Therefore, y = 9 Equation (1) becomes, x2 = 4 (9) = 36
∴ x = 6
Thus the two natural numbers are 6 and 9.
Q.7. Solve: x2 + 5√5x - 70 = 0
Ans:
Given, the equation is x2 + 5√5x - 70 = 0
We have to find whether the equation has real roots or not.
A quadratic equation ax2 + bx + c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero.
Discriminant = b2 - 4ac
Here, a = 1, b = 5√5 and c = -70
So, b2 - 4ac = (5√5)2 - 4(1)(-70)
= 125 + 280
= 405 > 0
So, the equation has 2 distinct real roots.
By using the quadratic formula,
x = [-b ± √b2 - 4ac]/2a
x = (-5√5 ± √405)/2(1)
= (-5√5 ± 9√5)/2
Now, x = (-5√5 + 9√5)/2 = 4√5/2 = 2√5
x = (-5√5 - 9√5)/2 = -14√5/2 = -7√5
Therefore, the roots of the equation are -7√5 and 2√5.
Q.8. A train travels a distance of 300 km at a uniform speed. If the speed of the train is increased by 5 km an hour, the journey would have taken two hours less. Find the original speed of the train.
Ans:
Total distance travelled = 300 km
Let the speed of train = x km/hr
We know that,
Hence, time taken by train = 300/x
According to the question,
Speed of the train is increased by 5km an hour
∴ the new speed of the train = (x + 5)km/hr
Time taken to cover 300km = 300/(x + 5)
Given that time taken is 2hrs less from the previous time
⇒ 300x + 1500 – 300x = 2x (x + 5)
⇒ 1500 = 2x2 + 10x
⇒ 750 = x2 + 5x
⇒ x2 + 5x – 750 = 0
⇒ x2 + 30x – 25x – 750 = 0
⇒ x (x + 30) – 25 (x + 30) = 0
⇒ (x – 25) (x + 30) = 0
⇒ (x – 25) = 0 or (x + 30) = 0
∴ x = 25 or x = – 30
Since, speed can’t be negative.
Hence, the speed of the train is 25km/hr
Q.9. The speed of a boat in still water is 11 km/ hr. It can go 12 km upstream and returns downstream to the original point in 2 hours 45 minutes. Find the speed of the stream.
Ans:
Let the speed of the stream be x km/hr
Given that, the speed boat in still water is 11 km/hr.
⇒ speed of the boat upstream = (11 - x) km/hr
⇒ speed of the boat downstream = (11 + x) km/hr
It is mentioned that the boat can go 12 km upstream and return downstream to its original point in 2 hr 45 min.
⇒ One-way Distance traveled by boat (d) = 12 km
⇒ Tupstream + Tdownstream = 2 hr 45 min = (2 + 3/4) hr = 11/4 hr
⇒ [distance / upstream speed ] + [distance / downstream speed] = 11/4
⇒ [ 12/ (11-x) ] + [ 12/ (11+x) ] = 11/4
⇒ 12 [ 1/ (11-x) + 1/(11+x) ] = 11/4
⇒ 12 [ {11 - x + 11 + x} / {121 - x2} ] = 11/4
⇒ 12 [ {22} / {121 - x2} ] = 11/4
⇒ 12 [ 2 / {121 - x2} ] = 1/4
⇒ 24 / {121 - x2} = 1/4
⇒ 24 (4) = {121 - x2}
⇒ 96 = 121 - x2
⇒ x2 = 121 - 96
⇒ x2 = 25
⇒ x = + 5 or -5
As speed to stream can never be negative, we consider the speed of the stream(x) as 5 km/hr. Thus, the speed of the stream is 5 km/hr.
Q.10. Determine the value of k for which the quadratic equation 4x2 - 3kx + 1 = 0 has equal roots.
Ans: The given equation 4x2 – 3kx + 1 = 0 is in the form of ax2 + bx + c = 0
Where a = 4, b = -3k, c = 1
For the equation to have real and equal roots, the condition is
D = b2 – 4ac = 0
⇒ (-3k)2 – 4(4)(1) = 0
⇒ 9k2 – 16 = 0
Q.11. Using quadratic formula, solve the following equation for ‘x’:
ab x2 + (b2 - ac) x - bc = 0
Ans:
We have: abx² + (b² − ac)x − bc = 0Here, A = ab, B = b² − ac, C = −bc
∴ x = −B ± √(B² − 4AC)2A
⇒ x = −(b² − ac) ± √((b² − ac)² − 4(ab)(−bc))2ab
⇒ x = −(b² − ac) ± √((b² − ac)² + 4ab²c)2ab
⇒ x = −(b² − ac) ± √(b⁴ − 2ab²c + a²c² + 4ab²c)2ab
⇒ x = −(b² − ac) ± (b² + ac)2ab or −(b² − ac) ± (b² − ac)2ab
⇒ x = 2ac2ab or −2b²2ab
⇒ x = cb or −ba
Q.12. The sum of the numerator and the denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes 1/2. Find the fraction.
Ans: Let’s assume the numerator of the fraction to be x and the denominator of the fraction to be y.
So, the required fraction is x/y.
From the question it’s given as, The sum of the numerator and denominator of the fraction is 12.
Thus, the equation so formed is,
x + y = 12
⇒ x + y – 12 = 0
And also it’s given in the question as,
If the denominator is increased by 3, the fraction becomes 1/2.
Putting this as an equation, we get
x/ (y + 3) = 1/2
⇒ 2x = (y + 3)
⇒ 2x – y – 3 = 0
The two equations are,
x + y – 12 = 0…… (i)
2x – y – 3 = 0…….. (ii)
Adding (i) and (ii), we get
x + y – 12 + (2x – y – 3) = 0
⇒ 3x -15 = 0
⇒ x = 5
Using x = 5 in (i), we find y
5 + y – 12 = 0
⇒ y = 7
Therefore, the required fraction is 5/7.
Q.13. Rewrite the following as a quadratic equation in x and then solve for x: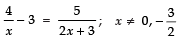
Ans: Given expression is
Solve the above expression
Cross multiplying the above equation
(4 – 3x) (2x + 3) = 5x
8x + 12 – 6x2 – 9x = 5x
– 6x2 + 8x – 9x – 5x + 12 = 0
– 6x2 – 6x + 12 = 0
Divide the above equation by -6 we get
x2 + x – 2 = 0
By following factorization method
x2 + 2x – x – 2 = 0
x (x + 2) -1(x + 2) = 0
(x + 2)(x – 1) = 0
x + 2 = 0 or x – 1= 0 x = -2, 1
The solution of the given expression is x = -2 and x = 1
Q.14. A two digit number is such that the product of its digits is 18. When 63 is subtracted from the number, the digits interchange their places. Find the number.
Ans: Let us consider, one’s digit of a two digit number = x and
Ten’s digit = y
The number is x + 10y
After interchanging the digits One’s digit = y
Ten’s digit = x
The number is y + 10x
As per the statement, xy = 18 ………(1)
And, x + 10y -63 = y + 10x
9y – 9x – y – 10x = 63
y – x = 7 …..(2)
using algebraic identity: (x + y)2 = (x – y)2 + 4xy
(x + y)2 = (-7)2 + 4(18) = 121 (Using (1))
(x + y)2 = 112
or x + y = 11 …..(3)
Add (1) and (2)
2y = 18
or y = 9
From (1): xy = 18
9x = 18
x = 2
Answer: The number is: x + 10y = 2 + 10(9) = 92
Q.15. A train covers a distance of 90 km at a uniform speed. Had the speed been 15 km/ hr more, it would have taken 30 minutes less for the journey. Find the original speed of the train.
Ans: Let the original speed of the train be x km/hr.
According to the question:90x − 90x + 15 = 12
⇒ 90(x + 15) − 90xx(x + 15) = 12
⇒ 90x + 1350 − 90xx² + 15x = 12
⇒ 1350x² + 15x = 12
⇒ 2700 = x² + 15x
⇒ x² + 15x − 2700 = 0
⇒ x² + (60 − 45)x − 2700 = 0
⇒ x(x + 60) − 45(x + 60) = 0
⇒ (x + 60)(x − 45) = 0
⇒ x = −60 or x = 45
x cannot be negative; therefore, the original speed of train is 45 km/hr.
Q.16. Solve for x: 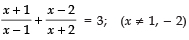
Ans: On cross multiply
(x + 1)(x + 2) + (x − 2)(x − 1) = 3(x − 1)(x + 2)
x2 + 3x + 2 + x2 − 3x + 2 = 3[x2 + x − 2]
2x2 + 4 = 3x2 + 3x − 6
x2 + 3x − 10 = 0
(x + 5)(x − 2) = 0
[x = 2, −5]
Q.17. Using quadratic formula, solve the following for x: 9x2 − 3 (a2 + b2) x + a2 b2 = 0
Ans:
Consider the equation: 9x² − 9(a + b)x + [2a² + 5ab + 2b²] = 0Comparing with Ax² + Bx + C = 0, we get:
A = 9, B = −9(a + b), and C = [2a² + 5ab + 2b²]Now, discriminant D = B² − 4AC
D = [−9(a + b)]² − 4 × 9 × [2a² + 5ab + 2b²]
= 9²(a + b)² − 36[2a² + 5ab + 2b²]
= 9[(a + b)² − 4(2a² + 5ab + 2b²)]
= 9[(a + b)² − (8a² + 20ab + 8b²)]
= 9[a² + b² + 2ab − 8a² − 20ab − 8b²]
= 9[(−7a² − 8b² − 18ab)]
= 9(a − b)²Using the quadratic formula: x = −B ± √D2A
Substituting values, we get:
x = 9(a + b) ± √[9(a − b)²]2 × 9⇒ x = 3(a + b) ± 3(a − b)6
Simplifying, we get:
x = (2a + 4b)6 or (a + 2b)3Hence, x = 2a + b3 and x = a + 2b3 are the required solutions.
Q.18. A number consisting of two digits is seven times the sum of its digits. When 27 is subtracted from the number, the digits are reversed. Find the number.
Ans: Let the tens and the units digits of the required number be x and y, respectively.
Required number = (10x + y)
10x + y = 7(x + y)
10x + 7y = 7x + 7y or 3x – 6y = 0 ……….(i)
Number obtained on reversing its digits = (10y + x)
(10x + y) - 27 = (10y + x)
⇒ 10x – x + y – 10y = 27
⇒ 9x – 9y = 27 ⇒9(x – y) = 27
⇒ x – y = 3 ……..(ii)
On multiplying (ii) by 6, we get:
6x – 6y = 18 ………(iii)
On subtracting (i) from (ii), we get:
3x = 18
⇒ x = 6
On substituting x = 6 in (i) we get
3 × 6 – 6y = 0
⇒ 18 – 6y = 0
⇒ 6y = 18
⇒ y = 3
Number = (10x + y) = 10 × 6 + 3 = 60 + 3 = 63
Hence, the required number is 63.
Q.19. The sum of the squares of two consecutive odd numbers is 394. Find the numbers.
Ans: Let the two consecutive odd numbers be x and x + 2.
∴ x2 + (x + 2)2 = 394
⇒ x2 + x2 + 4x + 4 = 394
⇒ 2x2 + 4x – 390 = 0
⇒ x2 + 2x – 195 = 0
⇒ x2 + 15x – 13x – 195 = 0
or
x(x + 15) – 13(x + 15) = 0
⇒ x= 13 or x = – 15
∴ For x = 13, x + 2 = 13 + 2 = 15
Thus, the required numbers are 13 and 15.
Q.20. Find the number which exceeds its positive square root by 20.
Ans: Let the Number be x
According to the given Question
√x + 20 = x
√x = x - 20
Squaring both the sides
x = x2 + 400 - 40x
[(a - b)2 = a2 - 2ab + b2]
x2 - 41x + 400 = 0
x2 - 16x - 25x + 400 = 0
x(x - 16) - 25(x - 16) = 0
(x - 16)(x - 25) = 0
Ans = x is equal to 25 or 16 both are correct answers
Q.21. A two digit number is such that the product of its digits is 14. If 45 is added to the number, the digits interchange their places. Find the number.
Ans: Let the no be 'xy' with x × y = 14
As xy + 45 = yx(x, y > 0)
⇒ (10x + y) + 45 = 10y + x
⇒ 9x − 9y + 45 = 0
⇒ x − y + 5 = 0 & x × y = 14
⇒ x− 14/x + 5 = 0
⇒ x − 14/x + 5 = 0
⇒ x2 + 5x − 14 = 0
⇒ x = 2,−7 & y = 7, −2
Ad x, y > 0 ⇒ no is 27
Q.22. A two digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number.
Ans: Let the one’s digit be ‘a’ and ten’s digit be ‘b’.
Given, two - digit number is such that the product of its digits is 20.
⇒ ab = 20 ----- (1)
Also, If 9 is added to the number, the digits interchange their places.
⇒ 10b + a + 9 = 10a + b
⇒ a – b = 1 ----- (2)
Substituting value of a from eq1 in to eq2
⇒ 20/b – b = 1
⇒ b2 + b – 20 = 0
⇒ (b + 5)(b – 4) = 0
Thus,
b = 4 and a = b + 1 = 5
Number is 45.
Q.23. A two digit number is such that the product of its digits is 15. If 8 is added to the number, the digits interchange their places. Find the number.
Ans: Let the ten's digit be x and one's digit be y.
The number will be 10x + y.
Given product of its digits is 15
xy = 15
y = 15/x --- (1).
Given that when 18 is added to the number the digits get interchanged.
10x + y + 18 = 10y + x
9x - 9y + 18 = 0
x - y + 2 = 0 ------- (2)
Substitute (1) in (2), we get
x - (15/x) + 2 = 0
x2 + 2x - 15 = 0
x2 + 5x - 3x - 15 = 0
x(x + 5) - 3(x + 5) = 0
(x + 5)(x - 3) = 0 x = -5, 3.
Since the digits cannot be negative, x = 3.
Substitute x = 3 in (1)
y = 15/3 = 5.
The number = 10x + y
= 10 * 3 + 5
= 30 + 5
= 35.
Q.24. Solve for x: abx2 + (b2 − ac) x − bc = 0
Ans:
We have:
abx2 + (b2 − ac)x − bc = 0Here, A = ab, B = b2 − ac, C = −bc
Using the quadratic formula:
x = −B ± √(B2 − 4AC)2ASubstituting values:
x = −(b2 − ac) ± √[(b2 − ac)2 − 4(ab)(−bc)]2ab⇒ x = −(b2 − ac) ± √[b4 − 2ab2c + a2c2 + 4ab2c]2ab
⇒ x = −(b2 − ac) ± √[(b2 + ac)2]2ab
Simplifying further:
x = 2ac2ab or x = −2b22abHence, x = cb or x = −ba
Q.25. The sum of two numbers is 18. The sum of their reciprocals is 1/4. Find the numbers.
Ans: Let The numbers be x and 18 - x
According to the given hypothesis:
1x + 118 − x = 14⇒ 18 − x + xx(18 − x) = 14
⇒ 72 = 18x − x2
⇒ x2 − 18x − 72 = 0
Factorizing:
x2 − 6x − 12x − 72 = 0⇒ x(x − 6) − 12(x − 6) = 0
⇒ (x − 6)(x − 12) = 0
⇒ x = 6 or x = 12
∴ The two numbers are 6 and 12.
Q.26. The sum of two numbers ‘a’ and ‘b’ is 15, and sum of their reciprocals 1/a and 1/b is 3/10. Find the numbers ‘a’ and ‘b’.
Ans: The two numbers are a and b
According to the question,
⇒ a + b = 15
⇒ a = 15 − b ---- ( 1 )
⇒ 1/a + 1/b = 3/10
⇒ 1/15−b + 1/b = 3/10
⇒ b + 15 − b/b(15 − b) = 3/10
⇒ 150 = 3b(15−b)
⇒ 50 = b(15 − b)
⇒ 50 = 15b − b2
⇒ b2 − 15b + 50 = 0
⇒ b2 − 10b − 5b + 50 = 0
⇒ b(b − 10) − 5(b − 10) = 0
⇒ (b − 10)(b − 5) = 0
∴ b = 5 or b = 10
Putting both values of b in equation ( 1),
⇒ a = 15 − 5 or a = 15 − 10
∴ a = 10 or a = 5
Q.27. Find the roots of the following quadratic equation: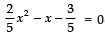
Ans: Given, 2/5 x2 - x - 3/5 = 0
⇒ 2x2 - 5x – 3 = 0
By splitting the middle term,
⇒ 2x2 - 6x + x – 3 = 0
Taking common in the expression,
⇒ 2x (x - 3) + 1 (x - 3) = 0
⇒ (2x + 1) (x - 3) = 0
∴ 2x + 1 = 0 and ∴ x – 3 = 0
∴ x = -1/2 and ∴ x = 3
Q.28. A natural number when subtracted from 28, becomes equal to 160 times its reciprocal.
Find the number.
Ans: Let the number be x
Now,
(28 - x) = 160 / x
28x - x2 = 160
x2 - 28x + 160 = 0
x2 - 20x - 8x + 160 = 0
x(x - 20) - 8(x - 20) = 0
(x - 8)(x - 20) = 0
x = 8 , 20
Q.29. Find two consecutive odd positive integers, sum of whose squares is 290.
Ans: Let one of the odd positive integer be x
then the other odd positive integer is x + 2
their sum of squares = x2 + (x + 2)2
= x2 + x2 + 4x + 4
= 2x2 + 4x + 4
Given that their sum of squares = 290
2x2 + 4x + 4 = 290
2x2 + 4x = 286
2x2 + 4x − 286 = 0
x2 + 2x − 143 = 0
x2 + 13x − 11x − 143 = 0
x(x + 13) − 11(x + 13) = 0
(x − 11) = 0,(x + 13) = 0
Therefore, x = 11 or −13
We always take positive value of x
So, x = 11 and (x + 2) = 11 + 2 = 13
Therefore , the odd positive integers are 11 and 13
Q.30. Find the values of k for which the quadratic equation
(k + 4) x2 + (k + 1) x + 1 = 0 has equal roots.
Also find these roots.
Ans: (k + 4)x2 + (k + 1)x + 1 = 0
D = b2 -4ac
= (k + 1)2 - 4(k + 4)(1)
= k2 + 2k + 1 - 4k - 16
= k2 - 2k - 15
For equal roots, D = 0
D = 0
K2 - 2k - 15 = 0
k2 - 5k + 3k - 15 = 0
k(k - 5) + 3(k - 5) = 0
(k + 3)(k - 5) = 0
k + 3 = 0
OR k - 5 = 0
k = -3, k = 5
Q.31. Solve for x: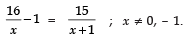
Ans:
16x − 1 = 15x + 1
⇒ 16 − xx = 15x + 1
Expanding: (16 − x)(x + 1) = 15x
⇒ 16x − x2 + 16 − x = 15x
⇒ x2 + 15x − 15x − 16 = 0
⇒ x2 = 16
⇒ x = ±4
Q.32. Solve for x: 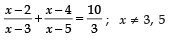
Ans:
In factorization, we write the middle term of the quadratic equation either as a sum of two numbers or difference of two numbers such that the equation can be factorized.
⇒ 3(x2 – 7x + 10) + 3(x2 – 7x + 12)
= 10(x2 – 8x + 15)
⇒ 4x2 – 38x + 84 = 0
⇒ 2x2 – 19x + 42 = 0
⇒ 2x2 – 12x – 7x + 42 = 0
⇒ 2x(x – 6) – 7(x – 6) = 0
⇒ (x – 6)(2x - 7) = 0
⇒ x = 7/2, 6
Q.33. Find the value of k, for which one root of quadratic equation kx2 – 14x + 8 = 0 is six times the other.
Ans: Let one root = α
Other root = 6αSum of roots = α + 6α = 14k
Or, 7α = 14k ⇒ α = 2k (i)
Product of roots: α × 6α = 8k
Or, 6α2 = 8k (ii)
Solving (i) and (ii):
6 × (2/k)28/k
⇒ 6 × 4k2 = 8k
⇒ 3k2 = 1k
Or, 3k = k2
Or, k(3 − k) = 0
⇒ k = 0 or k = 3
k = 0 is not possible.
Hence, k = 3
Q.34. If x = 2/3 and x = –3 are roots of the quadratic equation ax2 + 7x + b = 0, find the value of a and b.
Ans: Let us assume the quadratic equation be, Ax2 + Bx + C = 0.
Sum of the roots = -B/AGiven:
- Sum of roots = -7a = 23
Multiply both sides by a, we get:
-7 = 2a3
Solving for a:
a = 3
Product of roots = CA
Given:
ba = 23 × (-3)
Simplify:
b = -6
Q.35. If –5 is a root of the quadratic equation 2x2 + px – 15 = 0 and the quadratic equation p (x2 + x) + k = 0 has equal roots, find the value of k.
Ans: Given: -5 is a root of the quadratic equation 2x2 + px – 15 = 0
Substitute the value of x = -5
2(-5)2 + p(-5) – 15 = 0
50 – 5p – 15 = 0
35 – 5p = 0 p = 7
Again, In quadratic equation p(x2 + x) + k = 0
7 (x2 + x) + k = 0 (put value of p = 7)
7x2 + 7x + k = 0
Compare given equation with the general form of quadratic equation, which is ax2 + bx + c = 0
a = 7, b = 7, c = k
Find Discriminant:
D = b2 – 4ac
= (7)2 – 4 x 7 x k
= 49 – 28k
Since roots are real and equal, put D = 0
49 – 28k = 0
28k = 49 k = 7 / 4
The value of k is 7/4.
|
127 videos|584 docs|79 tests
|
FAQs on Worksheet Question and Solutions: Quadratic Equations Class 10 Worksheet Maths
| 1. What is a quadratic equation? |  |
| 2. How do I solve a quadratic equation using factorization? |  |
| 3. What is the quadratic formula and when should it be used? |  |
| 4. What does the discriminant tell us about the roots of a quadratic equation? |  |
| 5. Can a quadratic equation have complex roots? |  |