Some Application of Trigonometry Class 10 Worksheet Maths
Multiple Choice Questions
Q1: If the length of the shadow of a tree is decreasing then the angle of elevation is:
(a) Increasing
(b) Decreasing
(c) Remains the same
(d) None of the above
Ans: (a)
Sol:
As the shadow reaches from point D to C towards the direction of the tree, the angle of elevation increase from 30° to 60°.
Q2. The angle of elevation of the top of a building from a point on the ground, which is 30 m away from the foot of the building, is 30°. The height of the building is:
(a) 10 m
(b) 30/√3 m
(c) √3/10 m
(d) 30 m
Ans: (b) 30/√3 m
Sol: Say x is the height of the building.
a is a point 30 m away from the foot of the building.
Here, height is the perpendicular and distance between point a and foot of building is the base.
The angle of elevation formed is 30°.
Hence, tan 30° = perpendicular/base = x/30
1/√3 = x/30
x = 30/√3
Q3: If the height of the building and distance from the building foot’s to a point is increased by 20%, then the angle of elevation on the top of the building:
(a) Increases
(b) Decreases
(c) Do not change
(d) None of the above
Ans: (c)
Sol: We know, for an angle of elevation θ,
tan θ = Height of building/Distance from the point
If we increase both the value of the angle of elevation remains unchanged.
Q4: If a tower 6m high casts a shadow of 2√3 m long on the ground, then the sun’s elevation is:
(a) 60°
(b) 45°
(c) 30°
(d) 90°
Ans: (a)
Sol: As per the given question:
Hence,
tan θ = 6/2√3
tan θ = √3
tan θ = tan 60°
⇒ θ = 60°
Q5: The angle of elevation of the top of a building 30 m high from the foot of another building in the same plane is 60°, and also the angle of elevation of the top of the second tower from the foot of the first tower is 30°, then the distance between the two buildings is:
(a) 10√3 m
(b) 15√3 m
(c) 12√3 m
(d) 36 m
Ans: (a)
Sol: As per the given question: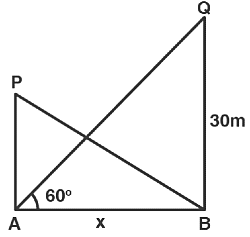
Hence,
tan 60° = 30/x
√3 = 30/x
x = 30/√3
x = 10√3m
Q6: The angle formed by the line of sight with the horizontal when the point is below the horizontal level is called:
(a) Angle of elevation
(b) Angle of depression
(c) No such angle is formed
(d) None of the above
Ans: (b) Angle of depression
Sol: The angle formed by the line of sight with the horizontal when the point is below the horizontal level is called angle of depression.
Q7: The angle formed by the line of sight with the horizontal when the point being viewed is above the horizontal level is called:
(a) Angle of elevation
(b) Angle of depression
(c) No such angle is formed
(d) None of the above
Ans: (a)
Sol: The angle formed by the line of sight with the horizontal when the point being viewed is above the horizontal level is called angle of elevation.
Q8: From a point on the ground, which is 15 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60°. The height of the tower (in m) standing straight is:
(a) 15√3
(b) 10√3
(c) 12√3
(d) 20√3
Ans: (a)
Sol: We know:
tan (angle of elevation) = height of tower/its distance from the point
tan 60° = h/15
√3 = h/15
h = 15√3
Q9: The line drawn from the eye of an observer to the point in the object viewed by the observer is said to be
(a) Angle of elevation
(b) Angle of depression
(c) Line of sight
(d) None of the above
Ans: (c)
Sol: The line drawn from the eye of an observer to the point in the object viewed by the observer is said to be line of sight.
Q10: The height or length of an object or the distance between two distant objects can be determined with the help of:
(a) Trigonometry angles
(b) Trigonometry ratios
(c) Trigonometry identities
(d) None of the above
Ans: (b)
Sol: The height or length of an object or the distance between two distant objects can be determined with the help of trigonometry ratios.
Solve the following Questions
Q1: Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide. From a point between them on the road the angles of elevation of the top of the poles are 60°and 30°.find the height of the poles and the distances of the point from the poles.
Ans: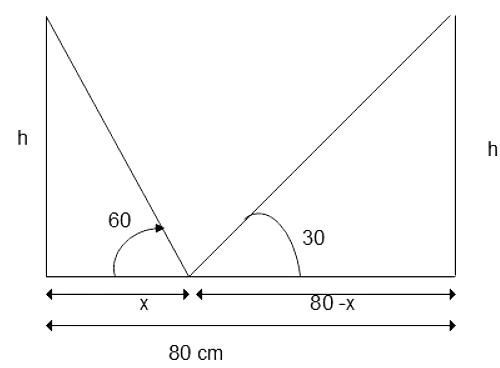
here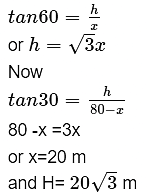
Q2: A tree standing on a horizontal plane leaning towards east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β .Prove that the height of the top from the ground is  .
.
Ans: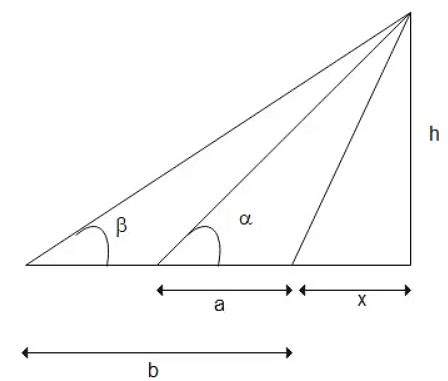
Here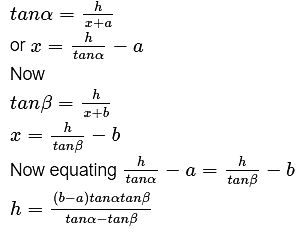
Q3: A man sitting at a height of 20m on a tall tree on a small island in the middle of the river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of tree. If the angles depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30° respectively. Find the width of the river.
Ans:
Here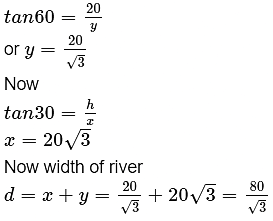
Q4: Consider right triangle ABC, right angled at B. If AC = 17 units and BC = 8 units determine all the trigonometric ratios of angle C.
Ans:
Given Data
Length of the side BC = 8 units
Length of the side AC = 17 units
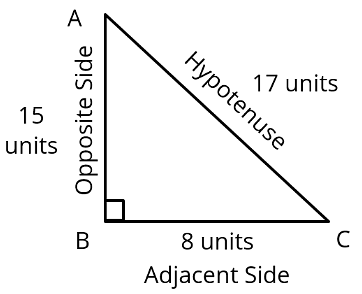
Step 1: Calculate the length of AB
In Δ ABC, using Pythagoras theorem, AB = 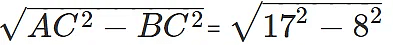
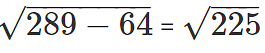
⇒ AB = 15 units
Step 2: Calculate the trigonometric ratios of angle C
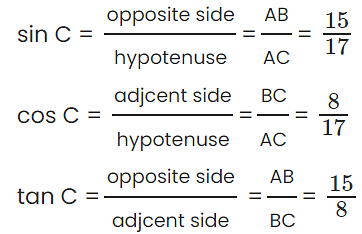
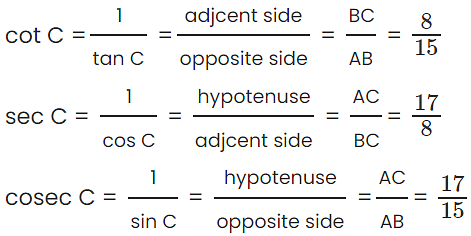
Q5: If C and Z are acute angles and that cos C = cos Z prove that ∠C = ∠Z.
Ans: Let us assume two right triangles ΔABC and ΔXYZ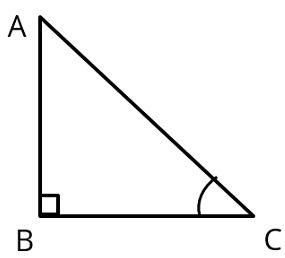
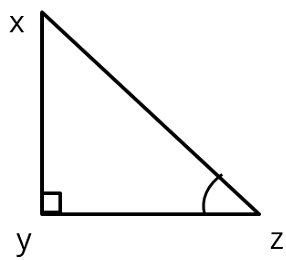
Given C and Z are acute angles and cos C = cos Z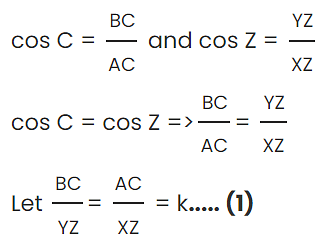
BC = k(yz) and AC = k(xz)
In right triangle ABC, using Pythagoras theorem AB = 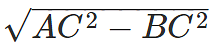
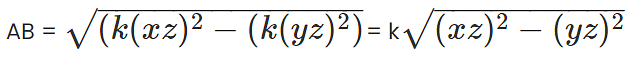
In right triangle xyz, using Pythagoras theorem xy = 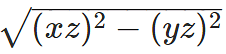

From 1 and 2,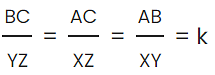
By SSS similarity criterion, we can conclude ΔABC is similar to ΔXYZ
∴ Corresponding angles of two similar triangles will be equal.
∴ ∠C = ∠Z
Q6: In triangle ABC, right angled at B if sin A = 1/2 . Find the value of
1. sin C cos A – cos C sin A
2. cos A cos C + sin A sin C
Ans: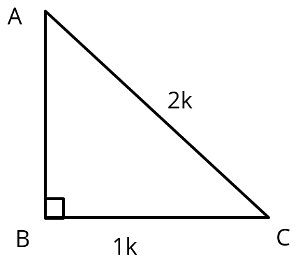

Let BC = k. Then, AC = 2k
Step 1: Compute Measure of side AB
Using Pythagoras theorem AB = 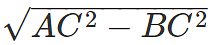

Step 2: Calculate the necessary trigonometric values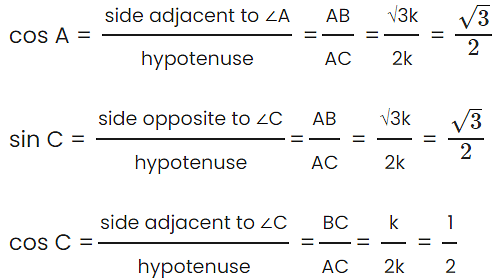
Step 3: Compute value of given expressions
(i) sin C cos A – cos C sin A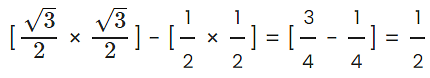
(ii) cos A cos C + sin A sin C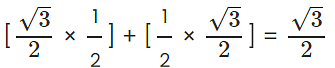
Q7: In triangle ABC right angled at B, AB = 12cm and ∠CAB = 60°. Determine the lengths of the other two sides.
Ans: Δ ABC is right angled at B
AB = 12 cm and ∠CAB = 60 °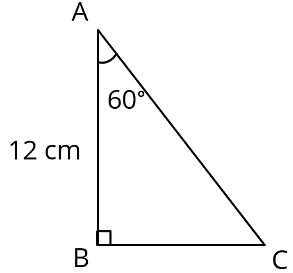
Part 1: Compute Length of AC
Let us use the trigonometric ratio involving AB and AC.
To angle ∠CAB, AB is the adjacent side.
AC is the hypotenuse of the triangle.
So, we will use cos ∠CAB.
cos ∠CAB = cos 60° = AB/AC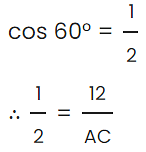
AC = 2 × 12 = 24 cm
So, AC = 24 cm
Part 2: Calculate Length of BC
Let us use the trigonometric ratio involving AB and BC.
To angle ∠CAB, AB is the adjacent side and BC is the opposite side.
So, we will use tan ∠CAB
tan ∠CAB = tan 60 ° = BC/AB
tan 60° = √3
√3 = BC/12
BC = 12 × √3 cm
Q8: If θ is an acute angle and  find θ.
find θ.
Ans: Divide both numerator and denominator of RHS by 2: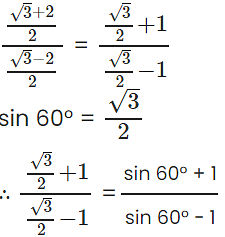
Compare the above result with LHS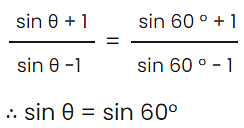
θ = 60°
Q9: Find the value of x in each of the following.
(i) cosec 3x = 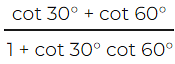
(ii) cos x = 2 sin 45° cos 45° – sin 30°
Ans: (i) cosec 3x = 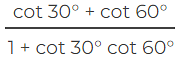
cot 30° = √3 ; cot 60° = 1/√3
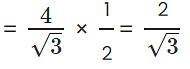
So, cosec 3x = 2/√3
We know 2/√3 = cosec 60°
cosec 3x = cosec 60°
∴ 3x = 60° or x = 20°
(ii) cos x = 2 sin 45° cos 45° – sin 30°
sin 45° = cos 45°= 1/√2; sin 30° = 1/2
cos x = 2 sin 45° cos 45° – sin 30°= 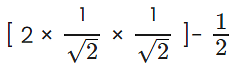
cos x = 1 - 1/2 = 1/2
We know cos 60° = 1/2
∴ cos x = cos 60° or x = 60°
Q10: Given sin A = 12/37, find cos A and tan A.
Ans: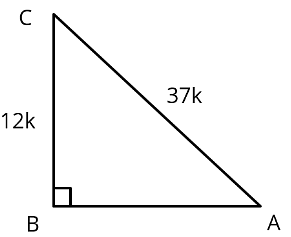

∴ If BC = 12k, AC = 37k
Using Pythagoras theorem AB = 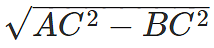
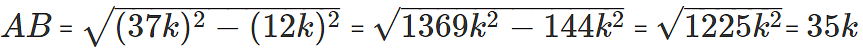

|
126 videos|457 docs|75 tests
|
FAQs on Some Application of Trigonometry Class 10 Worksheet Maths
| 1. What are the basic trigonometric ratios used in solving problems? |  |
| 2. How can I apply trigonometry to find the height of a building? |  |
| 3. What is the significance of the sine and cosine rules in trigonometry? |  |
| 4. Can you explain the concept of angle of elevation and angle of depression? |  |
| 5. What are some real-life applications of trigonometry? |  |






















