Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Standard) - 2 | Mathematics (Maths) Class 10 PDF Download
Class X
Mathematics – Standard
Sample Question Paper 2020-21
Max. Marks : 80
Duration : 3 hrs.
General Instructions :
1. This question paper contains two parts A and B.
2. Both Part A and Part B have internal choices.
Part – A :
1. It consists two sections - I and II.
2. Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
3. Section II has 4 questions on case study. Each case study has 5 case-based sub-parts. An examinee is to attempt any 4 out of 5 sub-parts.
Part – B :
1. Section III, Question No. 21 to 26 are Very short answer Type questions of 2 marks each.
2. Section IV, Question No. 27 to 33 are Short Answer Type questions of 3 marks each.
3. Section V, Question No. 34 to 36 are Long Answer Type questions of 5 marks each.
4. Internal choice is provided in 2 questions of 2 marks, 2 questions of 3 marks and 1 question of 5 marks.
Part - A
Sections - I
Section I has 16 questions of 1 mark each. Internal choice is provided in 5 questions.
Q.1. Calculate the largest number which divides 70 and 125, leaves remainders 5 and 8, respectively. (1 Mark)
OR
If p is a prime number, then find LCM of p, p2 and p3. (1 Mark)
Ans. Required largest number = HCF of (70 – 5) and (125 – 8) = HCF of 65 and 117 = 13
OR
p2 = p × p
p = p × 1
p3 = p × p × p
Required LCM = p × p × p = p3.
Q.2. Explain why 13233343563715 is a composite number? (1 Mark)
OR
A number is chosen at random from the numbers – 3, – 2, – 1, 0, 1, 2, 3. What will be the probability that square of this number is less than or equal to 1. (1 Mark)
Ans. Since, the given number ends in 5. Hence, it is a multiple of 5. Therefore, it is a composite number.
OR
No. of all possible outcomes = 7
No. of favourable outcomes = 3
The numbers whose square is ≤ 1 = – 1, 0, 1
∴ Required probability = 3 / 7
Q.3. How many polynomials can be formed with – 2 and 5 as zeroes? (1 Mark)
Ans. We know that if we divide or multiply a polynomial by any constant (real number), then the zeroes of polynomial remains same.
Here, a = −2 and b = +5
∴ α + β = −2 + 5 = 3 and
αβ = −2 × 5 = −10
So, required polynomial is x2 – (a + b)x + ab= x2 – 3x – 10
If we multiply this polynomial by any real number, let 5 and 2, we get 5x2 – 15x – 50 and 2x2 – 6x – 20 which are different polynomials but having same zeroes –2 and 5. So, we can obtain so many (infinite polynomials) from two given zeroes.
Q.4. Graphically, the pair of equations : (1 Mark)
6x – 3y + 10 = 0
2x – y + 9 = 0
Represents what kind of lines.
Ans. Here,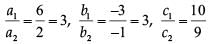
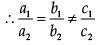
So, the system of linear equations is inconsistent (no solution) and graph will be a pair of parallel lines.
Q.5. Is the equation (√2x + √3)2 + x2 = 3x2 - 5x quadratic? Justify. (1 Mark)
Ans. (√2x)2 + (√3)2 + 2 x √2x x √3 + x2 = 3x2 - 5x
2x2 + 3 + 2√6x + x2 = 3x2 - 5x
3x2 + 2√6x + 3 = 3x2 - 5x
x(5 + 2√6) + 3 = 0
It is not of the form of ax2 +bx +c = 0.
So it is not a quadratic equation.
Q.6. Find the 30th term of the A.P., : 10, 7, 4 ................ (1 Mark)
Ans. In the given AP, a = 10 and d = 7 – 10 = –3
Thus, the 30th term is t30 = 10 + (30 − 1) (−3) = −77
Q.7. Find the distance of the point (– 3, – 4) from the x-axis (in units). (1 Mark)
Ans. The distance of the point (– 3, – 4) from x-axis = | – 4| = 4 units.
Q.8. In the given figure, if ∠AOB = 125°, then find ∠COD. (1 Mark)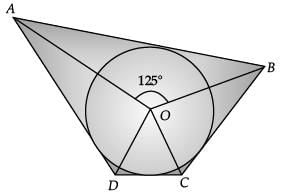
OR
In figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70°, then find ∠TRQ. (1 Mark)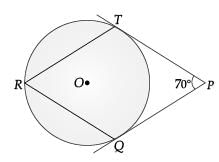 Ans. Since, quadrilateral circumscribing a circle subtends supplementary angles at the centre of the circle.
Ans. Since, quadrilateral circumscribing a circle subtends supplementary angles at the centre of the circle.
∴ ∠AOB + ∠COD = 180°
125° + ∠COD = 180°
∠COD = 180° – 125° = 55°
OR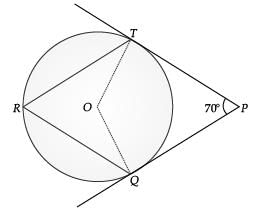 ∠TOQ = 180° – 70° = 110°
∠TOQ = 180° – 70° = 110°
(angle of supplementary)
Then, ∠TRQ = 1 / 2 ∠TOQ
(angle at the circumference of the circle by same arc)
= 1 / 2 x 110° = 55°.
Q.9. If the circumference of a circle and the perimeter of a square are equal, then find the relation between area of circle and area of square. (1 Mark)
Ans. According to question,
Circumference of a circle = Perimeter of square
Let ‘r’ and ‘a’ be the radius of circle and side of square respectively.
2πr = 4a
22 / 7 r = 2a
11r = 7a
r = 7a / 11 ..(i)
Area of circle, A1 = πr2
From equation (i), we have
A1 = π(7a / 11)2
= 22 / 7(49a2 / 121)
= 14a2 / 11 ...(ii)
Area of circle, A2 =a2 ...(iii)
From equation (ii) and (iii), we have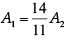
A1 > A2
Area of circle is greater than the area of square.
Q.10. During conversion of a solid from one shape to another, what will be the volume of new shape? (1 Mark)
Ans. During reshaping a solid, the volume of new solid will be equal to old one or remains unaltered.
Q.11. In the figure of DABC, the points D and E are onthe sides CA, CB respectively such that DE || AB, AD = 2x, DC = x + 3, BE = 2x – 1 and CE = x. Then, the value of x is ...................... . (1 Mark)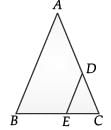 Ans.
Ans. 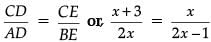
Using basic proportionality theorem
or, 5x = 3 or, x = 3 / 5
Detailed Answer :
In AB C, DE || AB
Then, CD / CA = CE / CB
or,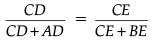
or,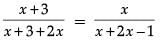
or,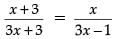
or, (x + 3)(3x – 1) = x(3x + 3)
or, 3x2 – x + 9x – 3 = 3x2 + 3x
or, 8x – 3 = 3x
or, 8x – 3x = 3
or, 5x = 3
∴ x = 3 / 5
Q.12. Find the value of sin260° + 2tan 45° – cos230°. (1 Mark)
OR
If sin A = 3 / 4, then find value of sec A. (1 Mark)
Ans. sin260º + 2 tan 45º – cos230º
(√3 / 2)2 + 2(1) - (√3 / 2)2
= 2
OR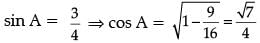
∴ sec A = 4 / √7
Q.13. Find the area (in cm2) of the circle that can be inscribed in a square of side 8 cm. (1 Mark)
Ans. 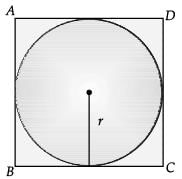 Side of square = diameter of circle = 8 cm
Side of square = diameter of circle = 8 cm
∴ Radius of circle, r = 8 / 2 = 4 cm
Area of circle = πr2
= π × 4 × 4 = 16πcm2
Q.14. The curved surface area of a cylinder is 264 m2 and its volume is 924 m3. Find the ratio of its height to its diameter. (1 Mark)
Ans. Curved Surface area of cylinder = 2πrh Volume of cylinder = πr2h
πr2h / 2πrh = 924 / 264 ⇒ r / 2 = 7 / 2
∴ r = 7 m
2πrh = 264
or, 2 x 22 / 7 x 7 x h = 264
or, h = 6 m
∴ h / 2r = 6 / 14 = 3 / 7
Hence, h : d = 3 : 7
Q.15. If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k? (1 Mark)
OR
Write the co-ordinates of a point P on x-axis which is equidistant from the points A(– 2, 0) and B (6, 0). (1 Mark)
Ans. Using distance formula,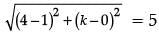
or 32 + k2 = 25
k = ± 4
OR
Using distance formula :
Point on x-axis is (2, 0)
Detailed Answer.
Let (x, 0) be equidistant from (– 2, 0) and (6, 0) by distant formula :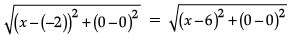
On squaring both sides,
(x + 2)2 = (x – 6)2
⇒ x2 + 4 + 4x = x2 + 36 – 12x
⇒ 4x + 12x = 36 – 4
⇒ 16x = 32
⇒ x = 2
Hence, the required point P(x, 0) = (2, 0)
Q.16. For the following distribution : (1 Mark)
Find the sum of lower limits of median class and modal class.
Ans. 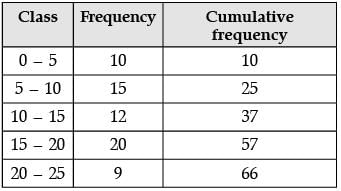
The modal class is the class having the maximum frequency.
The maximum frequency 20 belongs to class (15 – 20).
Here, n = 66
So, n / 2 = 66 / 2 = 33
33 lies in the class 10–15.
Therefore, 10 – 15 is the median class.
So, sum of lower limits of (15 – 20) and (10 – 15) is (15 + 10) = 25.
Section-II
Case study based questions are compulsory. Attempt any four sub parts of each question. Each subpart carries 1 mark
Q.17. Case Study based - 1 :
In a room, 4 friends are seated at the points A, B, C and D as shown in figure. Reeta and Meeta walk into the room and after observing for a few minutes Reeta asks Meeta.
Asks Meeta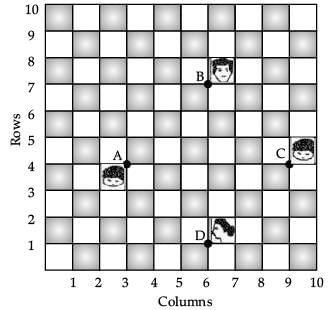
(a) What is the position of A? (1 Mark)
(i) (4, 3)
(ii) (3, 3)
(iii) (3, 4)
(iv) None of these
Ans. (iii)
Solution. Point A lies it x – 3, y = 4
A = (3, 4)
(b) What is the middle position of B and C? (1 Mark)
(i) (15 / 2, 11 / 2)
(ii) (2 / 15, 11 / 2)
(iii) (1 / 2, 1 / 2)
(iv) None of these
Ans. (i)
Solution. Mid point of B and C :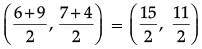
[∵ Co-ordinates of B = (6, 7) and C = (9 , 4)]
(c) What is the position of D? (1 Mark)
(i) (6, 0)
(ii) (0, 6)
(iii) (6, 1)
(iv) (1, 6)
Ans. (iii)
Solution. Point D lies at x = 6 and y = 1
D = (6, 1)
(d) What is the distance between A and B? (1 Mark)
(i) 3√2
(ii) 2√3
(iii) 2√2
(iv) 3√3
Ans. (i)
Solution. Since, A = (3, 4) and B = (6, 7)
Using distance formula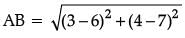
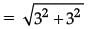
= √18 = 3√2 unit
(e) What is the equation of line CD? (1 Mark)
(i) x – y – 5 = 0
(ii) x + y – 5 = 0
(iii) x + y + 5 = 0
(iv) x – y + 5 = 0
Ans. (i)
Solution. Equation of line CD = Equation of line through C(9, 4) and D(6, 1)
i.e., 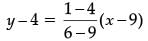
or, y – 4 = (x – 9)
or, x – y – 5 = 0
Q.18. Case Study based - 2 :
Seema placed a lighedbulb at point O on the ceiling and directly below it placed a table. Now, she put a cardboard of shape ABCD between table and lighted bulb. Then a shadow of ABCD is casted on the table as A'B'C'D' (see figure). Quadrilateral A'B'C'D' in an enlargement of ABCD with scale factor 1 : 2, Also, AB = 1.5 cm, BC = 25 cm, CD = 2.4 cm and AD = 2.1 cm; ∠A = 105°, ∠B = 100°, ∠C = 70° and ∠D = 85°.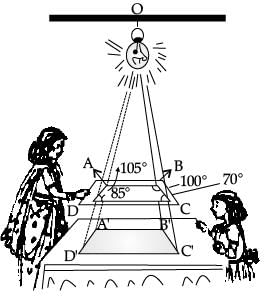
(a) What is the measurment of angle A'? (1 Mark)
(i) 105°
(ii) 100°
(iii) 70°
(iv) 80°
Ans. (i)
Solution. Quadrilateral A'B'C'D' is similar to ABCD.
∴ ∠A' = ∠A
⇒ ∠A' = 105°
(b) What is the length of A'B'? (1 Mark)
(i) 1.5 cm
(ii) 3 cm
(iii) 5 cm
(iv) 2.5 cm
Ans. (ii)
Solution. Given scale factor is 1 : 2
∴ A'B' = 2 AB
⇒ A'B' = 2 × 1.5 = 3 cm
(c) What is the sum of angles of quadrilateral A'B'C'D'? (1 Mark)
(i) 180°
(ii) 360°
(iii) 270°
(iv) None of these
Ans. (ii)
Solution. Sum of the angles of quadrilateral A'B'C'D' is 360°
(d) What is the ratio of sides A'B' and A'D'? (1 Mark)
(i) 5 : 7
(ii) 7 : 5
(iii) 1 : 1
(iv) 1 : 2
Ans. (i)
Solution. A'B' = 3 cm and A'D' = 2 AD
= 2 × 2.1 = 4.2 cm
∴ A'B' / A'D' = 3 / 4.2 = 30 / 42
= 5 / 7 = 5 : 7
(e) What is the sum of angles of C' and D'? (1 Mark)
(i) 105°
(ii) 100°
(iii) 155°
(iv) 140°
Ans. (iii)
Solution. C' = ∠C = 70°
and ∠D' = ∠D = 85°
∴ ∠C' + ∠D' = 70° + 85° = 155°
Q.19. Case Study based - 3 :
An electrician has to repaired and electric fault on the pole of height 5 cm. She needs to reach a point 1.3 m below the top of the pole to undertake the repair work (see figure)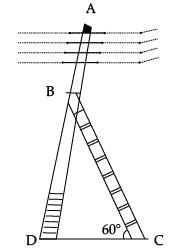
(a) What is the length of BD? (1 Mark)
(i) 1.3 m
(ii) 5 m
(iii) 3.7 m
(iv) None of these
Ans. (iii)
Solution. From figure, the electrician is required to reach at the point B on the pole AD.
So, BD = AD – AB = (5 – 1.3) m = 3.7 m
(b) What should be the length of Ladder, when inclined at an angle of 60° to the harizontal? (1 Mark)
(i) 4.28 m
(ii) 3.7 / √3 m
(iii) 3.7 m
(iv) 7.4 m
Ans. (i)
Solution. In ΔADC,
∴ sin 60° = BD / BC
⇒ √3 / 2 = 3.7 / BC
⇒ BC =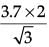
⇒ BC = 4.28 m (approx.)
(c) How far from the foot of pole should she place the foot of the ladder? (1 Mark)
(i) 3.7
(ii) 2.14
(iii) 1 / √3
(iv) None of these
Ans. (ii)
Solution. In DBDC,
∴ cot 60° = DC / BD
⇒ 1 / √3 = DC / 3.7
⇒ DC = 3.7 / √3
⇒ DC = 2.14 m (approx.)
(d) If the horizontal angle is changed to 30°, then what should be the length of the ladder? (1 Mark)
(i) 7.4 m
(ii) 3.7 m
(iii) 1.3 m
(iv) 5 m
Ans. (i)
Solution. In ΔBDC,
∴ sin 60° = BD / BC
⇒ 1 / 2 = 3.7 / BC
⇒ BC = 3.7 × 2 = 7.4 m
(e) What is the value of ∠B? (1 Mark)
(i) 60°
(ii) 90°
(iii) 30°
(iv) 180°
Ans. (iii)
Solution. In ΔADC, angle D is 90°.
So, by angle sum property.
∠B + ∠D + ∠C = 180°
or, ∠B = 180° – (90° + 60°)
= 30°
Q.20. Case Study based - 4 :
The weights (in kg) of 50 wrestlers are recorded in the following table :

(a) What is the upper limit of modal class. (1 Mark)
(i) 120
(ii) 130
(iii) 100
(iv) 150
Ans. (ii)
Solution. Modal Class = 120 – 130
Upper Unit = 130
(b) What is the mode of the given data (1 Mark)
(i) 21
(ii) 50
(iii) 25
(iv) 80
Ans. (i)
Solution. Mode of the given data is 21.
(c) How many wrestlers weights have more than 120 kg weight? (1 Mark)
(i) 32
(ii) 50
(iii) 16
(iv) 21
Ans. (i)
Solution. No. of wrestlers with more than 120 kg weight = 21 + 8 + 3 = 32
(d) What is the class mark for class 130 – 140? (1 Mark)
(i) 105
(ii) 125
(iii) 135
(iv) 145
Ans. (iii)
Solution. For class mark of 130 – 140,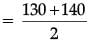
= 270 / 2 = 135
(e) Which method is more suitable to find the mean of the above data? (1 Mark)
(i) Direct method
(ii) Assumed mean method
(iii) Step-Deviation method
(iv) None of these
Ans. (iii)
Part - B
Section - III
All questions are compulsory. In case of internal choices, attempt any one.
Q.21. Write the denominator of the rational number 257 / 500 in the form 2m × 5n, where m and n are non-negative integers. Hence write its decimal expansion without actual division. (2 Mark)
Ans. Denominator = 500
= 22 × 53
Decimal expansion =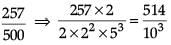
= 0.514
Q.22. In a rectangle ABCD, E is a point on AB such that AE = 2 / 3 AB. If AB = 6 km and AD = 3 km, then find DE. (2 Mark)
Ans. In ΔCAB, ∠A = ∠B (Given)
∴ AC = CB
(By isosceles triangle property)
But, AD = BE (Given) ...(i)
Or, AC – AD = BC – BE
∴ CD = CE ...(ii)
Dividing equation (ii) by (i),
CD / AD = CE / BE
By converse of BPT,
DE || AB.
OR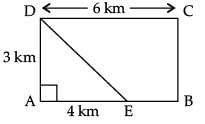 Given, AE = 2 / 3 AB = 2 / 3 x 6 = 4 km
Given, AE = 2 / 3 AB = 2 / 3 x 6 = 4 km
In right angled triangle ADE,
DE2 = (3)2 + (4)2
or, DE2 = 25
∴ DE = 5 km.
Q.23. If sin (A + B) = 1 and sin (A – B) = 1 / 2, 0 ≤ A + B = 90° and A > B, then find A and B. (2 Mark)
OR
Express : sin A and tan A in terms of sec A. (2 Mark)
Ans. Here, sin (A + B) = 1 = sin 90º
or, A + B = 90º ...(i)
sin (A – B) = 1 / 2 = sin 30º
or, A – B = 30º ...(ii)
Solving eqns. (i) and (ii),
A = 60º and B = 30º
OR
(i) sin A =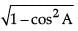
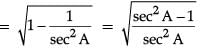

(ii) tan2A = secA – 1
or,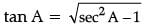
Q.24. An observer 1.5 m tall is 28.5 m away from a tower 30 m high. Find the angle of elevation of the top of the tower from his eye. (2 Mark)
Ans. 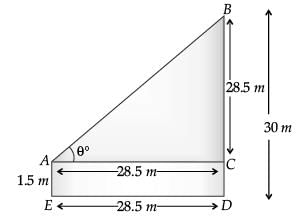 AE be observer = 1.5 m
AE be observer = 1.5 m
BD is the tower = 30 m
∠BAC = θ, BC = 30 – 1.5 = 28.5 m
In ΔBAC, BC / AC = tan θ
⇒ 28.5 / 28.5 = tan θ
⇒ tan θ = 1 = tan 45°
⇒ θ = 45°
Hence, the angle of elevation is 45°.
OR
Let BD = x m and DC = y m.
From ΔABD, ∠D = 90°
7√3 / x = tan 30°
⇒ 7√3 / x = 1 / √3
⇒ 7√3 x √3
= 21 m
From ΔADC, ∠D = 90°
7√3 / y = tan 60°
⇒ 7√3 = y√3
⇒ y = 7 m,
BC = BD + DC
= 21 + 7 = 28 m.
Hence, the value of BC = 28 m.
Q.25. A child prepares a poster on "save water" on a square sheet whose each side measures 50 cm. At each corner of the sheet, she draws a quadrant of radius 15 cm in which she shows the ways to save water. At the centre, she draws a circle of diameter 21 cm and writes a slogan save water in it. Find the area of the remaining sheet. (2 Mark)
Ans. Side of square= 50 cm
∴ Area of square = 50 × 50 = 2500 cm2 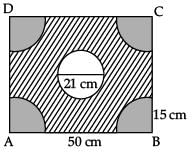
Radius of quadrant = 15 cm.
Area of 4 quadrants = 4 x 1 / 4 πr2 = πr2
= π × 15 × 15
= 22 / 7 x 225
= 707.14 cm2
Area of circle = πr2
= 22 / 7 x (21 / 2)2
= 22 / 7 x 21 / 2 x 21 x 2
= 346.5 cm2
Area of remaining sheet = Area of square – 4(area of quadrant) – Area of circle
= 2500 – 707.14 – 346.5
= 1446.36 sq. cm
Q.26. A teacher took a surprise test of maths. He observes the marks of five students of class. He observes the median is 45.5 and mode is 50.5. So find the mean of the marks of five students using an empirical formula. (2 Mark)
OR
Find the mode of the following frequency distribution (2 Mark)
Ans. Given, Mode = 50.5
Median = 45.5
3 Median = Mode + 2 Mean
⇒ 3 × 45.5 = 50.5 + 2 Mean
⇒ Mean =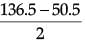
Hence, Mean = 43.
OR
Maximum frequency = 16,
Modal class is 30 – 40
Mode =

= 36
Section - IV
All questions are compulsory. In case of internal choices, attempt any one.
Q.27. Sum of the ages of a father and the son is 40 years. If father ’s age is three times that of his son, then find their respective ages. (3 Mark)
OR
A part of monthly hostel charge is fixed and the remaining depends on the number of days one has taken food in the mess. When Swati takes food for 20 days, she has to pay ₹ 3,000 as hostel charges whereas Mansi who takes food for 25 days has to pay ₹ 3,500 as hostel charges. Find the fixed charges and the cost of food per day. (3 Mark)
Ans. Let age of father and son be x and y respectively.
Then, x + y = 40 ...(i)
and x = 3y ...(ii)
By solving eqns. (i) and (ii), we get
x = 30 and y = 10
Thus, the ages of father and son are 30 years and 10 years.
OR
Let fixed charge be x and per day food cost be y
Then, x + 20y = 3000 ...(i)
and x + 25y = 3500 ...(ii)
Subtracting (i) from (ii), we get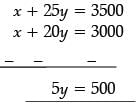
y = 100 Substituting this value of y in (i), we get
x + 20(100) = 3000 x = 1000
∴ x = 1000 and y = 100
Hence, fixed charge and cost of food per day are ₹ 1,000 and ₹ 100.
Q.28. The ninth term of an A.P. is equal to seven times the second term and twelfth term exceeds five times the third term by 2. Find the first term and the common difference. (3 Mark)
OR
The sum of first n terms of three arithmetic progressions are S1, S2 and S3 respectively. The first term of each A.P. is 1 and common differences are 1, 2 and 3 respectively. Prove that S1 + S3 = 2S2. (3 Mark)
Ans. Let the first term of A.P. be a and common difference be d.
Given, a9 = 7a2
or, a + 8d = 7(a + d) ...(i)
a + 8d = 7a + 7d – 6a + d = 0 ...(iii)
and a12 = 5a3 + 2
Again, a + 11d = 5(a + 2d) + 2 ...(ii)
a + 11d = 5a + 10d + 2 – 4a + d = 2 ...(iv)
Subtracting (iv) from (iii), we get – 2a = – 2
or, a = 1
From (iii),
– 6 + d = 0
d = 6
Hence, first term = 1 and common difference = 6
OR
Since, S1 = 1 + 2 + 3 + .... + n.
S2 = 1 + 3 + 5 + ...upto n terms
and S3 = 1 + 4 + 7 + ...upto n terms
or, S1 = n(n + 1) / 2
Also,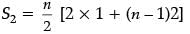
= n / 2[2n] = n2
and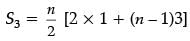
= n(3n - 1) / 2
Now, 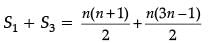
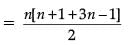
= n[4n] / 2
= 2n2 = 2S2
Hence Proved.
Q.29. A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon form the edges of the girl at any instant of 60°. After sometime, the angle of elevation reduces to 30°. (3 Mark)
(i) Find the distance travelled by the balloon during the interval.
(ii) Which mathematical concept is used in the above problem ?
Ans. (i) Let P be the position of the balloon when its angle of elevation from the eyes of the girl is 60° and Q be the position when angle of elevation is 30°.
In ΔOLP, tan 60° = PL / OL
⇒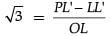
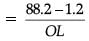
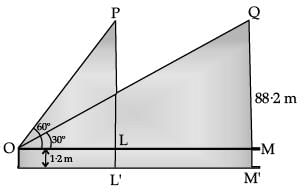 ⇒ √3 = 87 / OL
⇒ √3 = 87 / OL
⇒ OL = 87 / √3
In ΔOMQ, tan 30° = QM / OM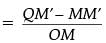
⇒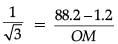
⇒ OM = 87√3
∴ Distance travelled by the balloon,
PQ = LM = OM – OL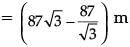
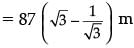
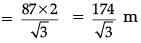

(ii) Height and distance.
Q.30. If (x2 + y2)(a2 + b2) = (ax + by)2. Prove that x / a + y / b. (3 Mark)
Ans. Given, (x2 + y2)(a2 + b2) = (ax + by)2
⇒ x2a2 + x2b2 + y2a2 + y2b2 = a2x2 + b2y2 + 2abxy
⇒ x2b2 + y2a2 – 2abxy = 0
⇒ (xb – ya)2 = 0
[∵ (a - b)2 = a2 + b2 - 2ab]
⇒ xb = ya
∴ x / a + y / b
Hence proved
Q.31. A bag contains 18 balls out of which x balls are red. (3 Mark)
(i) If one ball is drawn at random from the bag, what is the probability that it is not red ?
(ii) If 2 more red balls are put in the bag, the probability of drawing a red ball will be 9 / 8 times the probability of drawing a red ball in the first case. Find the value of x.
Ans. P(red ball) = x / 18
(i) P(no red ball) =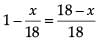
(ii) Now, Total number of balls = 18 + 2 = 20
Total number of Red balls = x + 2
P(red balls) =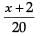
Now, According to the question,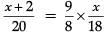
⇒ 180x = 144x + 288
⇒ 36x = 288
⇒ x = 288 / 36 = 8
Q.32. In the given figure, OP is equal to the diameter of a circle with centre O and PA and PB are tangents. Prove that ABP is an equilateral triangle. (3 Mark)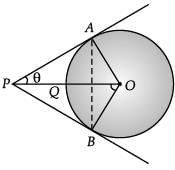 Ans. Construction : Join A to B.
Ans. Construction : Join A to B.
We have,
OP = diameter
⇒ OQ + QP = diameter
⇒ Radius + QP = diameter
⇒ OQ = PQ = radius
Thus, OP is the hypotenuse of right angled ∆AOP.
So, In ∆AOP, sin θ = AO / OP = 1 / 2
θ = 30°
Hence, ∠APB = 60°
Now, in ∆ABP, AP = PB
So, ∠PAB = ∠PBA = 60°
∴ ∆APB is an equilateral triangle.
Q.33. If bcos θ = a, then prove that cosec θ + cot θ =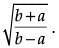 (3 Mark)
(3 Mark)
Ans. 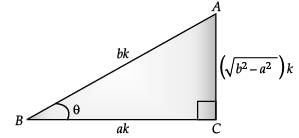 Given, cos θ = a / b
Given, cos θ = a / b
AC2 = AB2 – BC2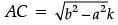
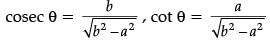

Hence proved.
Section - V
All questions are compulsory. In case of internal choices, attempt any one.
Q.34. Solve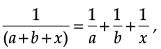 where a + b ≠ 0. (5 Mark)
where a + b ≠ 0. (5 Mark)
OR
Check whether the equation 5x2 – 6x – 2 = 0 has real roots and if it has, find them by the method of completing the square. Also, verify that roots obtained satisfy the given equation. (5 Mark)
Ans.
Given,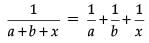
⇒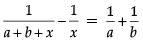
⇒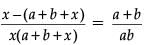
⇒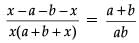
⇒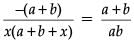
⇒ x(a + b+ x) = – ab
⇒ x2 + (a + b)x + ab = 0
⇒ (x + a)(x + b) = 0
⇒ x = – a or x = – b
OR
Discriminant ⇒ b2 – 4ac.
Here, a = 5, b = (– 6) and c = (– 2)
Then, b2 – 4ac = (– 6)2 – 4 × 5 × – 2
= 36 + 40 = 76 > 0
So the equation has real and two distinct roots.
Again, 5x2 – 6x = 2 (dividing both the sides by 5)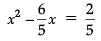
On adding square of the half of coefficient of x
⇒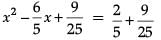
⇒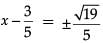
⇒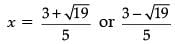
Verification :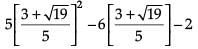
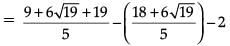
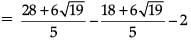
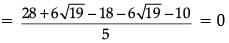
Similarly,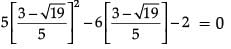
Hence, Verified.
Q.35. In the given figure, D and E trisect BC. Prove that 8AE2 = 3AC2 + 5AD2. (5 Mark)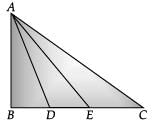
Ans. Let BD = DE = EC be x
BE = 2x
and BC = 3x
Now, in ΔABE,
AE2 = AB2 + BE2
= AB2 + 4x2, ...(i)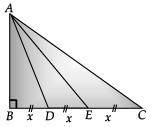
In ΔABC,
AC2 = AB2 + BC2 = AB2 + 9x2
In ΔADB, and AD2 = AB2 + BD2 = AB2 + x2
Now, on multiplying (i) by 8,
8AE2 = 8AB2 + 32x2 ...(ii)
and 3AC2 + 5AD2 = 3(AB2 + 9x2) + 5 (AB2 + x2)
= 3AB2 + 27x2 + 5AB2 + 5x2
= 8AB2 + 32x2 = 8 (AB2 + 4x2)
∴ 3AC2 + 5AD2 = 8AE2. [From eqns. (i)]
Hence proved.
Q.36. A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 20 cm and the diameter of the cylinder is 7 cm. Find the total volume of the solid. (π = 22 / 7) (5 Mark)
Ans. Height of cylinder= 20 – 7 = 13 cm.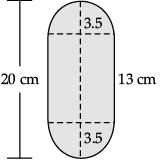 Total volume =
Total volume = 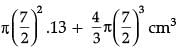
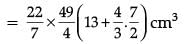
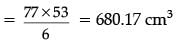
Detailed Solution :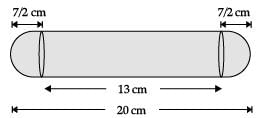
Height of the cylinder(h)= (20 – 7) cm = 13 cm
Radius of circular part(r) = 7 / 2 cm
Volume of solid = Volume of cylinder + 2 × Volume of hemisphere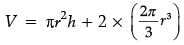
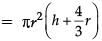
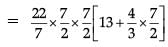
= 77 / 2(53 / 3)cm3
= 680.17 cm3
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper (2020-21) (Standard) - 2 - Mathematics (Maths) Class 10
| 1. What is the CBSE Sample Question Paper for Class 10 Mathematics? |  |
| 2. How can students benefit from solving the CBSE Sample Question Paper? |  |
| 3. Where can I find the CBSE Sample Question Paper for Class 10 Mathematics? |  |
| 4. Are the questions in the CBSE Sample Question Paper similar to the actual exam questions? |  |
| 5. How should students approach solving the CBSE Sample Question Paper? |  |





















