Mechanical Properties of Fluids: Part 2 | Physics Class 11 - NEET PDF Download
Archimedes' Principle
- Archimedes made a significant discovery regarding how objects behave when immersed in a fluid, whether partially or completely.
- He found that such objects experience a buoyant force equal to the weight of the fluid they displace.
- This observation led to the formulation of Archimedes' principle, which is fundamentally rooted in the principles of fluid statics.
- When an object is submerged in a fluid, the fluid exerts pressure on the object's surface, creating a force perpendicular to the surface at every point.
- This force is determined by the pressure at that point multiplied by the area of the surface.
- The overall effect of these forces results in a net upward force known as buoyancy or upthrust.
Understanding the Forces at Play
To comprehend how buoyancy works, let's consider a scenario where an object is immersed in a fluid with a certain density.
The forces acting on the vertical sides of the object will balance each other out. However, the top and bottom surfaces of the object experience different forces due to the varying pressure at different depths.
- Force on the Top Surface: The top surface of the object experiences a downward force due to the pressure at that depth. This force can be calculated using the formula:

where A is the area, h1 is the depth of the top surface, and (𝜎𝑔+𝑃0) represents the pressure at that point.
- Force on the Bottom Surface: The bottom surface of the object experiences an upward force due to the pressure at that greater depth. This force is given by:

where h2 is the depth of the bottom surface.
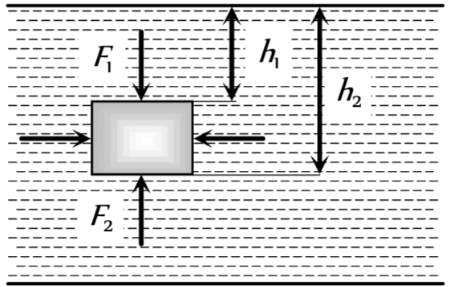
- Since the pressure increases with depth (h2 > h1), the upward force (𝑭𝑢𝑝) will be greater than the downward force (𝑭𝑑𝑜𝑤𝑛).
- This difference in forces leads to a net upward force on the object, calculated as:
- 𝑭𝑛𝑒𝑡 = 𝑭𝑢𝑝 − 𝑭𝑑𝑜𝑤𝑛 = 𝑉ρ (g2 − g1)
- This net force can also be expressed in terms of the volume of fluid displaced by the object.
- If L is the height of the object, then:
- 𝑭𝑛𝑒𝑡 = Vρ = gρ
- where V is the volume of fluid displaced.
- This force, representing the weight of the displaced fluid, is what we refer to as buoyancy or upthrust.
- Buoyancy acts vertically upwards, opposing the weight of the object, and its point of action is through the center of gravity of the displaced fluid.
- This principle explains why objects feel lighter in water and why some objects float while others sink.
- Though we have derived this result for a body fully submerged in a fluid, it can be shown to hold good for partly submerged bodies or a body in more than one fluid also.
- Upthrust is independent of all factors of the body such as its mass, size, density, etc. except the volume of the body inside the fluid.
- Upthrust depends upon the nature of displaced fluid. This is why upthrust on a fully submerged body is more in seawater than in fresh water because its density is more than fresh water.
- Apparent weight of the body of density ρ when immersed in a liquid of density σ.


- If a body of volume V is immersed in a liquid of density σ, then its weight reduces.


- Relative density of a body (R.D.) is the ratio of the density of the body to the density of water. It can also be defined as:

Floatation
(1) Translatory equilibrium
When a body with density ρ and volume V is immersed in a liquid with density σ, the forces acting on the body are:
The weight of the body: W = mg = V ρ g, which acts vertically downward through the center of gravity of the body.
The upthrust force: V σ g, which acts vertically upward through the center of buoyancy (the center of gravity of the displaced liquid).
(a) If density of body is greater than that of liquid ρ>σ:
- Weight will be more than upthrust so the body will sink.
(b) If density of body is equal to that of liquid ρ=σ:
- Weight will be equal to upthrust so the body will float fully submerged in neutral equilibrium with its top surface in it just at the top of the liquid.

(c) If density of body is lesser than that of liquid ρ<σ:
- Weight will be less than upthrust so the body will move upwards, and in equilibrium, will float partially immersed in the liquid.

W = Vinρg
⇒V ρg = Vinσg

(2) Rotational Equilibrium
- When a floating body is slightly tilted from its equilibrium, the center of buoyancy B shifts.
- The new vertical line through the shifted center of buoyancy B′ intersects the original vertical line at a point called the meta-center M.
- If this meta-center is located above the center of gravity, the forces at G (weight of the body W) and B′ (upthrust) create a restoring couple that returns the body to its original position.
- Therefore, for a floating body to maintain rotational equilibrium, the meta-center must always be higher than the center of gravity.
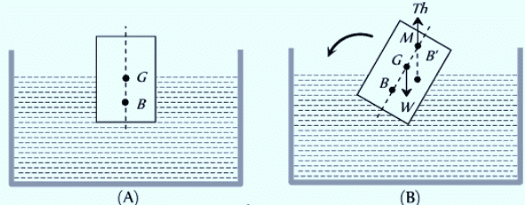
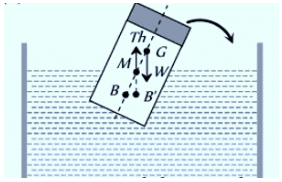
- If the meta-center falls below the center of gravity, the forces at G (weight) and B′ (upthrust) will create a couple that causes the floating body to topple.
- That is why a wooden log cannot be made to float vertical in water or a boat is likely to capsize if the sitting passengers stand on it.
- In these situations, CG becomes higher than MG and so the body will topple if slightly tilted.
Applications of floatation
(i) When a body floats, the weight of the body equals the upthrust. Therefore:

Thus, the volume outside the liquid is:

This gives the fraction of volume outside the liquid:

(ii) For flotation:

(iii) If the same body floats in different liquids with densities σA and σB, respectively:


Streamline, Laminar and Turbulent Flow
 (i) Streamline Flow
(i) Streamline Flow
Streamline flow of a liquid occurs when each element of the liquid passing through a point follows the same path and has the same velocity as the preceding element at that point.

- A streamline is the path, straight or curved, where the tangent at any point indicates the direction of the flow of liquid at that point.
- Two streamlines cannot intersect, and when streamlines are closer together, it indicates a higher velocity of the liquid particles at that location.
- The path ABC in the figure represents a streamline, with v1, v2, and v3 being the velocities of the liquid at points A, B, and C, respectively.
(2) Laminar Flow
Laminar flow occurs when a liquid flows over a horizontal surface in steady layers with different velocities that do not mix with one another. This type of flow is referred to as laminar flow.
In laminar flow, the velocity of the liquid is always lower than its critical velocity. Laminar flow is often used interchangeably with streamlined flow.
(3) Turbulent Flow
When a liquid flows at a speed higher than its critical velocity, the motion of its particles becomes chaotic or irregular. This type of flow is called turbulent flow.
- In turbulent flow, both the path and velocity of liquid particles change continuously and unpredictably over time.
- Most of the external energy that maintains turbulent flow is used to create swirling motions (eddies) within the liquid, leaving only a small amount of energy for forward motion.
- For example, eddies can be seen around the pillars of a bridge over a river.

Critical Velocity and Reynold's Number
The critical velocity is the speed up to which the flow of liquid remains streamlined, and above this velocity, the flow becomes turbulent.
Reynolds number is a dimensionless number that indicates the nature of the flow of a liquid through a pipe.
It is defined as the ratio of the inertial force per unit area to the viscous force per unit area for a fluid in motion.

If a liquid with density ρ flows through a tube of radius r and cross-sectional area A, the mass of the liquid flowing per second is given by:

If the value of Reynold's number
(i) When the Reynolds number is between 0 and 2000, the liquid flow is streamlined or laminar.
(ii) When the Reynolds number is between 2000 and 3000, the liquid flow becomes unstable and transitions from streamlined to turbulent.
(iii) When the Reynolds number is above 3000, the liquid flow is definitely turbulent.
Equation of Continuity
The equation of continuity is derived from the principle of conservation of mass.


- This expression is known as the equation of continuity for the steady flow of an incompressible and non-viscous liquid.
- The velocity of the flow does not depend on the type of liquid (assuming it is non-viscous).
- The velocity of the flow increases when the cross-sectional area decreases and decreases when the cross-sectional area increases. This explains:
(a) In hilly regions, where rivers are narrow and shallow (i.e., small cross-section), the water flows faster. In contrast, in plains, where rivers are wider and deeper (i.e., large cross-section), the water flows slower, making the deeper water appear still.
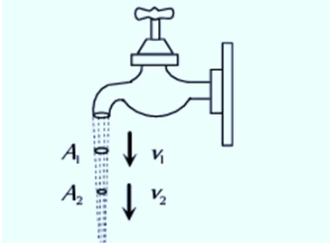
(b) When water falls from a tap, the velocity of the falling water increases with distance due to the action of gravity (i.e., v2 > v1). According to the equation of continuity, the cross-sectional area of the water stream decreases (i.e., A2 < A1), meaning the stream of falling water becomes narrower.
Energy of a Flowing Fluid
A flowing fluid in motion possesses the following three types of energy:

If you hang two balloons vertically with separate threads and blow out air with your mouth in between the gap of two balloons, to your surprise the balloons will come closer to each other rather than going far off. This is an illustration of Bernoulli's Equation, which we are going to study in detail in this document.

Bernoulli's Principle
It states that:
The sum of pressure energy, kinetic energy and potential energy per unit volume of an incompressible, non-viscous fluid in a streamlined irrotational flow remains constant along a streamline.
Mathematically, it can be expressed as, 
Proof of Bernoulli's Principle
Assumptions:
- The fluid is incompressible, non-viscous, non-rotational, and streamlined flow.
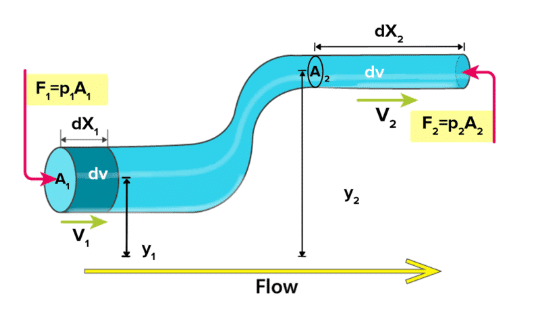
- Mass of the fluid entering from side S
dm1 = p A1 dx1 = p dV1 - The work done in this displacement dx1 at point S is
Wp1 = F1dx1 = P1A1dx1
Wp1 = P1dV1 {∵ A1dx1 = dV1}
At the same time, the amount of fluid that moves out of the tube at point T is dm2 = pdV2
According to the equation of continuity 
The work done in the displacement of dm2 mass at point T
Wp2 = P2dV2
Now Apply the Work - Energy Theorem,





h = Gravitational head = volume head
= volume head
Bernoulli’s Equation at Constant Depth
When the fluid moves but its depth is constant—that is, .
Under that condition, Bernoulli’s equation becomes:

Bernoulli’s Equation for Static Fluids
When the fluid is static, then v1 = v2 = 0, then Bernoulli’s equation is given as:
When v1 = v2 = 0 | P1 + ρgh1 = P2 + ρgh2 |
When h2 = 0 | P2 = P1 + ρgh1 |
Application of Bernoulli's principle
1. Magnus effect
- When a spinning ball is thrown, it deviates from its usual path in flight. This effect is called the Magnus effect and plays an important role in tennis, cricket, soccer, etc., as by applying appropriate spin the moving ball can be made to curve in any desired direction.
- If a ball is moving from left to right and also spinning about a horizontal axis perpendicular to the direction of motion as shown in the figure, then relative to the ball air will be moving from right to left.
 (a)
(a)  (b)
(b)  (c)
(c)
- The resultant velocity of air above the ball will be V + rw while below it V - rw (shown in figure).
- So in accordance with Bernoulli's principle pressure above the ball will be less than below it.
- Due to this difference of pressure, an upward force will act on the ball and hence the ball will deviate from its usual path OA0 and will hit the ground at A1 following the path OA1 (figure shown).
- i.e., if a ball is thrown with backspin, the pitch will curve less sharply prolonging the flight.
- Similarly, if the spin is clockwise, i.e., the ball is thrown with topspin, the force due to pressure difference will act in the direction of gravity and so the pitch will curve more sharply shortening the flight.
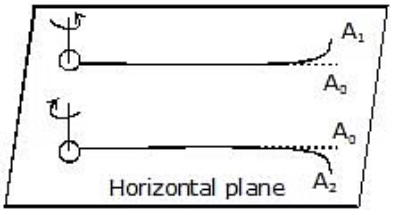
Furthermore, if the ball is spinning about a vertical axis, the curving will be sideways as shown in the figure. producing the so-called out swing or in the swing.
2. Action of Atomiser
- The action of the aspirator, carburetor, paint gun, scent spray, or insect sprayer is based on Bernoulli's principle.
- In all these, by means of motion of a piston P in a cylinder C, high-speed air is passed over a tube T dipped in liquid L to be sprayed.
- High-speed air creates low pressure over the tube, due to which liquid (paint, scent, insecticide, or petrol) rises in it and is then blown off in very small droplets with expelled air.

3. Working of Aeroplane
- This is also based on Bernoulli's principle.
- The wings of the aeroplane have tapering as shown in the figure.
- Due to this specific shape of wings when the airplane runs, air passes at higher speed over it as compared to its lower surface.
- This difference of air speeds above and below the wings, in accordance with Bernoulli's principle, creates a pressure difference, due to which an upward force called 'dynamic lift' ( = pressure difference × area of the wing) acts on the plane.
- If this force becomes greater than the weight of the plane, the plane will rise up.

Example 1: If pressure and velocity at point A are P1 and V1 respectively & at point B is P2, V2 is the figure as shown. Comment on P1 and P2.
Sol: From the equation of continuity A1V1 = A2V2
here A1 > A2
⇒ V1 < V2 ....(1)
from Bernoulli's equation. We can write
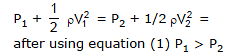
Torricelli's Law of Efflux (Velocity of efflux)
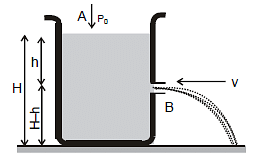
The cross-sectional area of the hole at A is greater than B If water comes in the tank with velocity vA and goes outside with velocity

On Applying Bernoulli's theorem at A and B,
Range (R)
Let us find the range R on the ground.
Considering the vertical motion of the liquid.
(H -h) =  or
or 
Now, considering the horizontal motion,
R = vt or  or
or 
From the expression of R, the following conclusions can be drawn,
(i) Rh = RH -h
as  and
and 
This can be shown in Figure.
(ii) R is maximum at H/2 and R max = H.
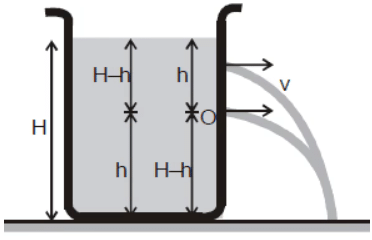
Proof: R2 = 4 (H h – h2)
For R to be maximum, 
or H - 2h = 0 or h = H/2
That is, R is maximum at h=H/2
and 
Example 2: A cylindrical dark 1 m in radius rests on a platform 5 m high. Initially, the tank is filled with water up to a height of 5 m. A plug whose area is 10–4 m2 is removed from an orifice on the side of the tank at the bottom Calculate
(a) the initial speed with which the water flows from the orifice
(b) the initial speed with which the water strikes the ground and
(c) time taken to empty the tank to half its original volume
(d) Does the time to empty the tank depend upon the height of the stand?
Sol: The situation is shown in the figure:
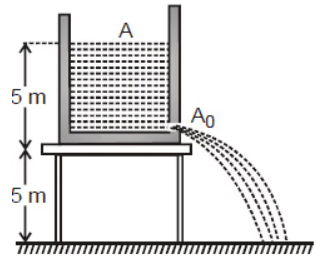
(a) As the speed of flow is given by


(b) As the initial vertical velocity of water is zero, so is its vertical velocity when it hits the ground
So the initial speed with which water strikes the ground.

(c) When the height of the water level above the hole is y, the velocity of flow will be  and so the rate of flow
and so the rate of flow


Which on integration improper limits gives


= 9.2 × 103s – ~ 2.5 h
(d) No, as an expression of t is independent of the height of the stand.
4. Venturimeter
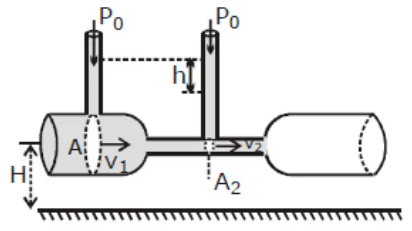
The figure shows a venturi meter used to measure flow speed in a pipe of non-uniform cross-section.
We apply Bernoulli's equation to the wide (point 1) and narrow (point 2) parts of the pipe, with h1 = h2

From the continuity equation

Substituting and rearranging, we get
Because A1 is greater than A2, v2 is greater than v1 and hence the pressure P2 is less than P1.
A net force to the right acceleration the fluid as it enters the narrow part of the tube (called the throat) and a net force to the left slows as it leaves.
The pressure difference is also equal to ρgh, where h is the difference in liquid level in the two tubes. Substituting in Eq. (1), we get

5. Pivot Tube
- It is a device used to measure the flow velocity of fluid.
- It is a U-shaped tube that can be inserted in a tube or in the fluid-flowing space as shown in the figure shown.
- In the U tube, a liquid that is immiscible with the fluid is filled up to a level C and the short opening M is placed in the fluid flowing space against the flow.
- This allows a few of the fluid particles to enter into the tube and exert a pressure on the liquid in limb A of U tube.
- Due to this, the liquid level changes as shown in the figure shown.
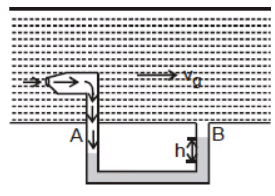
- At end B fluid is freely flowing, which exerts approximately negligible pressure on this liquid. The pressure difference at ends A and B can be given by measuring the liquid level difference h as it is a gas, then PA - PB = ρhg
- It is the liquid of density, then PA - PB = h(ρ - ρg)g
- Now if we apply Bernoulli's equation at the ends of A and B we'll have

Now by using equations, we can evaluate the velocity v, with which the fluid is flowing.
Note: A pivot tube is also used to measure the velocity of airplanes with respect to the wind. It can be mounted at the top surface of the plain and hence the velocity of wind can be measured with respect to the plane.
6. Siphon
It is a pipe used to drain liquid at a lower height but the pipe initially rises and then comes down

let velocity of outflow be v and the pipe is of uniform cross-section A. Applying Bernoulli's Equation between P (top of the tank) and R (Opening of pipe) we get

⇒ 
here velocity is considered zero at P since the area of the tank is very large compared to the area of the pipe

Naturally for siphon to work
h1 > 0
Now as the area of the pipe is constant by the equation of continuity
as Av = constant the velocity of flow inside the siphon is also constant between Q and R
(P + pgh + 1/2 pv2)Q = (P + pgh + 1/2 pv2)R ⇒ PQ + pgh2 = P0 - pgh1 (v is same)
⇒ PQ = P0 - Pg (h1 + h2) as PQ = 0 ⇒ P0 > pg (h1 + h2) means (h1 + h2) should not be more than P/pg for siphon to work.
Viscosity
- The property of a fluid by virtue of which an internal frictional force acts between its different layers which opposes their relative motion is called viscosity.
- These internal frictional force is called viscous force.

- Viscous forces are inter-molecular forces acting between the molecules of different layers of liquid moving with different velocities.
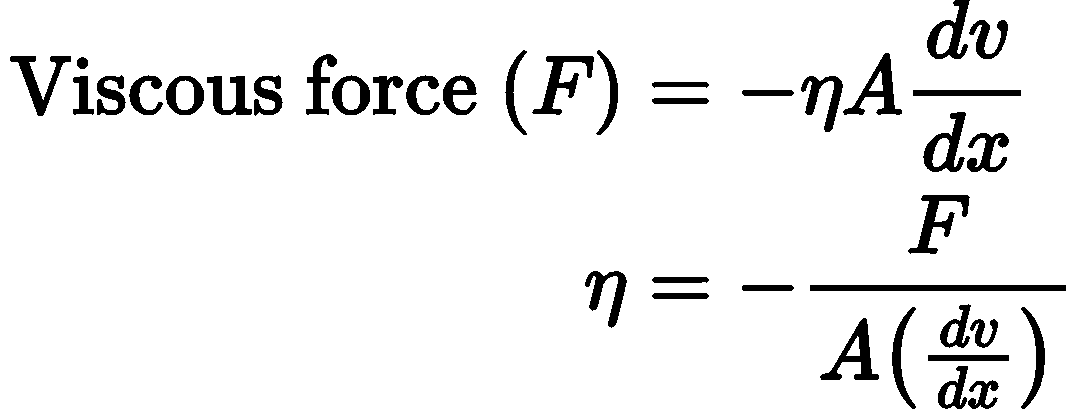
where, (dv/dx) = rate of change of velocity with distance called velocity gradient, A = area of cross-section and = coefficient of viscosity.
- SI unit of η is Nsm-2 or pascal-second or decapoise. Its dimensional formula is [ML-1T-1].
- The knowledge of the coefficient of viscosity of different oils and its variation with temperature helps us to select a suitable lubricant for a given machine.
- Viscosity is due to transport of momentum. The value of viscosity (and compressibility) for ideal liquid is zero.
- The viscosity of air and of some liquids are utilised for damping the given parts of some instruments.
- The knowledge of viscosity of some organic liquids is used in determining the molecular weight and shape of large organic moleculars like proteins and cellulose.
Variation of Viscosity
- The viscosity of liquids decreases with increase in temperature

where, η0 and ηt is are coefficient of viscosities at 0°C and t°C, α and β are constants.
- The viscosity of gases increases with increase in temperatures as η ∝ √T
- The viscosity of liquids increases with increase in pressure but the viscosity of water decreases with increase in pressure.
- The viscosity of gases do not changes with pressure.
Poiseuille’s Formula
The rate of flow (v) of liquid through a horizontal pipe for steady flow is given by


where, p = pressure difference across the two ends of the tube. r = radius of the tube, n = coefficient of viscosity.
This is known as Poiseuille's equation.
The Rate of Flow of Liquid
Rate of flow of liquid through a tube is given by v = (P/R)
where, R = (8 ηl/πr4), called liquid resistance and p = liquid pressure.
- Series combination of Tubes



- Parallel combination of tubes



Stoke's Law
When a sphere moves through a thick liquid, like honey, the resistance it faces depends on how fast it's moving, how big the sphere is, and how thick the liquid is. This resistance is called Stokes' drag.
Imagine stirring honey with a spoon—the harder and faster you stir (velocity), the bigger the spoon (radius), and the thicker the honey (viscosity), the more resistance you feel.

This resistance force is calculated using a formula that takes into account the viscosity of the liquid, the size of the sphere, and how fast it's moving.

- where F is the frictional force — known as Stokes' drag — acting on the interface between the fluid and the particle
- η is the viscosity
- R is the radius of the spherical object
- V is the flow velocity
Tips and Tricks to Learn:
- When a liquid is in equilibrium, the force on its surface is perpendicular everywhere.
- In a liquid, the pressure is uniform at the same horizontal level.
- Pressure is the same in all directions at any point within a liquid.
- The pressure is perpendicular to the surface of the fluid.
- The pressure at any point in a liquid depends on its depth (h), density, and acceleration due to gravity.
- Pressure is independent of the shape of the container or the total mass of the liquid.
- Force is a vector quantity, while pressure is a tensor quantity.
- Pressure and density in fluids play the same role as force and mass do in solids.
- Bar and millibar are units used for measuring pressure in meteorology.
- A sudden drop in atmospheric pressure indicates a storm.
- The first scientific weather forecast was made using a water barometer constructed in the 17th century by Von Guericke, who predicted a storm after a sudden fall in the water column height.

|
97 videos|378 docs|103 tests
|
FAQs on Mechanical Properties of Fluids: Part 2 - Physics Class 11 - NEET
| 1. What is Archimedes' Principle and how does it apply to floating objects? |  |
| 2. What is the difference between streamline, laminar, and turbulent flow? |  |
| 3. How does Bernoulli's Principle relate to the energy of a flowing fluid? |  |
| 4. What is the equation of continuity and how does it apply to fluid flow? |  |
| 5. What are some practical applications of Bernoulli's Principle? |  |

|
Explore Courses for NEET exam
|

|