NCERT Exemplar: Quadratic Equations - 2 | Mathematics (Maths) Class 10 PDF Download
Exercise 4.4
Q.1. Find whether the following equations have real roots. If real roots exist, find them.
(i) 8x2 + 2x – 3 = 0
(ii) –2x2 + 3x + 2 = 0
(iii) 5x2 – 2x – 10 = 0
(iv) 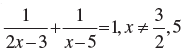
(v) x2 + 5√5x- 70 = 0
(i) Given, the quadratic equation is 8x² + 2x - 3 = 0
We have to find whether the equation has real roots or not.
A quadratic equation ax² + bx + c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero.
Discriminant = b² - 4ac
Here, a = 8, b = 2 and c = -3
So, b² - 4ac = (2)² - 4(8)(-3)
= 4 + 96
= 100 > 0
So, the equation has 2 distinct real roots.
By using the quadratic formula,
x = [-b ± √b² - 4ac]/2a
x = (-2 ± √100)/2(8)
= (-2 ± 10)/16
Now, x = (-2 + 10)/16 = 8/16 = 1/2
x = (-2 - 10)/16 = -12/16 = -3/4
Therefore, the roots of the equation are 1/2 and -3/4(ii) Given, the quadratic equation is -2x² + 3x + 2 = 0
We have to find whether the equation has real roots or not.
A quadratic equation ax² + bx + c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero.
Discriminant = b² - 4ac
The equation can be rewritten as -(2x² - 3x - 2) = 0
2x² - 3x - 2 = 0
Here, a = 2, b = -3 and c = -2
So, b² - 4ac = (-3)² - 4(2)(-2)
= 9 + 16
= 25 > 0
So, the equation has 2 distinct real roots.
By using the quadratic formula,
x = [-b ± √b² - 4ac]/2a
x = (3 ± √25)/2(2)
= (3 ± 5)/4
Now, x = (3 + 5)/4 = 8/4 = 2
x = (3 - 5)/4 = -2/4 = -1/2
Therefore, the roots of the equation are -1/2 and 2.(iii) Given, the quadratic equation is 5x² - 2x - 10 = 0
We have to find whether the equation has real roots or not.
A quadratic equation ax² + bx + c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero.
Discriminant = b² - 4ac
Here, a = 5, b = -2 and c = -10
So, b² - 4ac = (-2)² - 4(5)(-10)
= 4 + 200
= 204 > 0
So, the equation has 2 distinct real roots.
By using the quadratic formula,
x = [-b ± √b² - 4ac]/2a
x = (2 ± √204)/2(5)
= (2 ± 2√51)/10
Now, x = (2 + 2√51)/10 = 2(1+√51)/10 = (1+√51)/5
x = (2 - 2√51)/10 = 2(1-√51)/10 = (1-√51)/5
Therefore, the roots of the equation are (1+√51)/5 and (1-√51)/5.(iv) Given, the equation is 1/(2x-3) + 1/(x-5) = 1
We have to find whether the equation has real roots or not.
The equation can be rewritten as
(x - 5) + (2x - 3) = (x -5)(2x - 3)
x - 5 + 2x - 3 = 2x² - 3x - 10x + 15
3x - 8 = 2x² - 13x + 15
By grouping,
2x² - 13x - 3x + 15 + 8 = 0
2x² - 16x + 23 = 0
A quadratic equation ax² + bx + c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero.
Discriminant = b² - 4ac
Here, a = 2, b = -16 and c = 23
So, b² - 4ac = (-16)² - 4(2)(23)
= 256 - 184
= 72 > 0
So, the equation has 2 distinct real roots.
By using the quadratic formula,
x = [-b ± √b² - 4ac]/2a
x = (16 ± √72)/2(2)
= (16 ± 6√2)/4
Now, x = (16 + 6√2)/4 = 2(8+3√2)/4 = (8+3√2)/2 = 2(4+3√2/2)/2 = 4+3√2
x = (2 - 6√2)/4 = 2(1-3√2)/4 = (1-3√2)/2 = 2(4-3√2/2)/2 = 4-3√2
Therefore, the roots of the equation are (4+3√2/2) and (4-3√2/2)(v) Given, the equation is x² + 5√5x - 70 = 0
We have to find whether the equation has real roots or not.
A quadratic equation ax² + bx + c = 0 has 2 distinct real roots when the discriminant of the equation is greater than zero.
Discriminant = b² - 4ac
Here, a = 1, b = 5√5 and c = -70
So, b² - 4ac = (5√5)² - 4(1)(-70)
= 125 + 280
= 405 > 0
So, the equation has 2 distinct real roots.
By using the quadratic formula,
x = [-b ± √b² - 4ac]/2a
x = (-5√5 ± √405)/2(1)
= (-5√5 ± 9√5)/2
Now, x = (-5√5 + 9√5)/2 = 4√5/2 = 2√5
x = (-5√5 - 9√5)/2 = -14√5/2 = -7√5
Therefore, the roots of the equation are -7√5 and 2√5.
Q.2. Find a natural number whose square diminished by 84 is equal to thrice of 8 more than the given number.
Let the natural number = ‘x’.
According to the question,
We get the equation,
x² – 84 = 3(x + 8)
x² – 84 = 3x + 24
x² – 3x – 84 – 24 = 0
x² – 3x – 108 = 0
x² – 12x + 9x – 108 = 0
x(x – 12) + 9(x – 12) = 0
(x + 9) (x – 12)
⇒ x = -9 and x = 12
Since, natural numbers cannot be negative.
The number is 12.
Q.3. A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.
Let the natural number = x
When the number increased by 12 = x + 12
Reciprocal of the number = 1/x
According to the question, we have,
x + 12 = 160 times of reciprocal of x
x + 12 = 160/ x
x( x + 12 ) = 160
x2 + 12x – 160 = 0
x2 + 20x – 8x – 160 = 0
x( x + 20) – 8( x + 20)= 0
(x + 20) (x – 8) = 0
x + 20 = 0 or x – 8 = 0
x = – 20 or x = 8
Since, natural numbers cannot be negative.
The required number = x = 8
Q.4. A train, travelling at a uniform speed for 360 km, would have taken 48 minutes less to travel the same distance if its speed were 5 km/h more. Find the original speed of the train.
Let original speed of train = x km/h
We know,
Time = distance/speed
According to the question, we have,
Time taken by train = 360/x hour
And, Time taken by train its speed increase 5 km/h = 360/( x + 5)
It is given that,
Time taken by train in first – time taken by train in 2nd case = 48 min = 48/60 hour
360/x – 360/(x +5) = 48/60 = 4/5
360(1/x – 1/(x +5)) = 4/5
360 ×5/4 (5/(x² +5x)) =1
450 × 5 = x² + 5x
x² +5x -2250 = 0
x = (-5± √ (25+9000))/2
= (-5 ±√ (9025) )/2
= (-5 ± 95)/2
= -50, 45
But x ≠ -50 because speed cannot be negative
So, x = 45 km/h
Hence, original speed of train = 45 km/h
Q.5. If Zeba were younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than five times her actual age. What is her age now?
Let Zeba’s age = x
According to the question,
(x-5)²=11 + 5x
x² + 25 - 10x = 11 + 5x
x² - 15x + 14 = 0
x² - 14x - x + 14 = 0
x(x -14) -1(x - 14) = 0
x = 1 or x = 14
We have to neglect 1 as 5 years younger than 1 cannot happen.
Therefore, Zeba’s present age = 14 years.
Q.6. At present Asha’s age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha.
Given, at present Asha’s age is 2 more than the square of her daughter Nisha’s age.
Also, when Nisha grows to her mother’s present age, Asha’s age will be one year less than 10 times the present age of Nisha.
We have to find the present age of both Asha and Nisha.
Let the age of Nisha be x.
Then, Asha’s age = x² + 2
As per given condition,
(x² + 2) + [(x² + 2) - x] = 10x - 1
2x² + 4 - x - 10x + 1 = 0
2x² - 11x + 5 = 0
On factoring,
2x² + 10x - x + 5 = 0
2x(x + 5) - 1(x - 5) = 0
(2x - 1)(x - 5) = 0
Now, 2x - 1 = 0
2x = 1
x = 1/2
Also, x - 5 = 0
x = 5
Age of Nisha = 1/2 years is not possible.
So, the age of Nisha = 5 years.
Age of Asha = (5)² + 2 = 25 + 2 = 27 years.
Therefore, the present ages of Nisha and Asha are 5 years and 27 years.
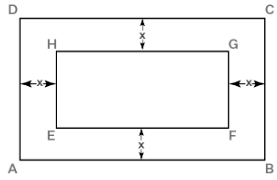
Q.7. In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular
pond has to be constructed so that the area of the grass surrounding the pond
would be 1184 m2 [see Fig.]. Find the length and breadth of the pond.
Given, the dimensions of the rectangular lawn is 50m × 40m.
Area of the grass surrounding the pond is 1184 m².
We have to determine the length and breadth of the pond.
Let ABCD be the rectangular lawn and EFGH be the rectangular pond.
Let x m be the width of the grass area around the pond.
So, length of the lawn = 50 m
Breadth of the lawn = 40 m
Length of the pond = (50 - 2x)m
Breadth of the pond = (40 - 2x)m
Area of grass = area of lawn - area of pond
1184 = (50 × 40) - [(50 - 2x) × (40 - 2x)]
1184 = 2000 - [2000 - 100x - 80x + 4x²]
1184 = 2000 - 2000 + 100x + 80x - 4x²
1184 = 180x - 4x²
So, 4x² - 180x + 1184 = 0
Dividing by 4,
x² - 45x + 296 = 0
On factoring,
x² - 37x - 8x + 296 = 0
x(x - 37) - 8(x - 37) = 0
(x - 8)(x - 37) = 0
Now, x - 8 = 0
x = 8
Also, x - 37 = 0
x = 37
When x = 37, the length of the pond = 50 - 2(37) = 50 - 74 = -24
So, x = 37 is not possible.
Therefore, the width of the grass area is 8 m.
Now, length of the pond = 50 - 2(8) = 50 - 16 = 34 m
Breadth of the pond = 40 - 2(8) = 40 - 16 = 24m
Therefore, the length and breadth of the pond is 34 and 24m.
Q.8. At t minutes past 2 pm, the time needed by the minutes hand of a clock to show
3 pm was found to be 3 minutes less than t2/4 minutes. Find t.
Given, at t minutes past 2 pm time needed by the minute hand to show 3pm was 3 minutes less than t²/4 minutes.
We have to find the value of t.
Time taken by the minute hand to travel from 2 pm to 3 pm = 60 minutes
So, t minutes past 2, the time needed to show 3 is 60-t.
As per given condition,
60 - t = (t²/4 - 3)
60 - t = (t² - 12)/4
240 - 4t = t² - 12
t² + 4t - 12 - 240 = 0
t² + 4t - 252 = 0
On factoring,t² - 14t + 18t - 252 = 0
t(t - 14) + 18(t - 14) = 0
(t + 18)(t - 14) = 0
Now, t - 14 = 0
t = 14
Also, t + 18 = 0
t = -18
Since time cannot be negative, t = -18 is neglected.
Therefore, the value of time t is 14 minutes.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Quadratic Equations - 2 - Mathematics (Maths) Class 10
| 1. What is a quadratic equation? |  |
| 2. How can we solve a quadratic equation? |  |
| 3. What is the discriminant of a quadratic equation? |  |
| 4. Can a quadratic equation have only one solution? |  |
| 5. What are the applications of quadratic equations in real life? |  |