Class 10 Maths Chapter 1 Previous Year Questions - Real Numbers
Previous Year Questions 2025
Q1: If (-1)n + (-1)8 = 0, then n is: (2025)
(a) any positive integer
(b) any negative integer
(c) any odd number
(d) any even number
 View Answer
View Answer 
Ans: (c)
We have,
(-1)n + (-1)8 = 0 ⇒ (-1)n + 1 = 0 ⇒ (-1)n = (-1)
On comparing the powers, we get n = 1, 3, 5, ..........
∴ Hence, n is any odd number.
Q2: Which of the following cannot be the unit digit of 8n, where n is a natural number? (2025)
(a) 4
(b) 2
(c) 0
(d) 6
 View Answer
View Answer 
Ans: (c)
8n = (2 × 2 × 2)n
Since, factors of 8n do not contain 5 in it.
So, 8n can't ends with 0.
⇒ 0 can't be the unit digit of 8n.
Q3: If x is the LCM of 4, 6, 8 and y is the LCM of 3, 5, 7 and p is the LCM of x and y, then which of the following is true? (2025)
(a) p = 35x
(b) p = 4y
(c) p = Bx
(d) p = 16y
 View Answer
View Answer 
Ans: (a)
LCM (4, 6, 8) = x = 24
LCM (3, 5, 7) = y= 105
LCM (x, y) = p = LCM (24, 105) = 840
∴ p = 840 = 35 × 24 = 35x
Q4: If HCF (98, 28) = m and LCM (98, 28) = n, then the value of n - 7m is: (2025)
(a) 0
(b) 28
(c) 98
(d) 198
 View Answer
View Answer 
Ans: (c)
98 = 2 × 72, 28 = 22 × 7
∴ LCM (98, 28) = 22 × 72 = 196
⇒ n = 196
HCF (98, 28) = 2 × 7 = 14
⇒ m = 14
∴ n - 7m = 196 - 7 × 14 = 196 - 98 = 98
Q5: The greatest number which divides 70 and 125, leaving remainders 5 and 8 respectively, is: (2025)
(a) 13
(b) 65
(c) 875
(d) 1750
 View Answer
View Answer 
Ans: (a)
We have to find the H.C.F of 70 - 5 = 65 and 125 - 8 = 117.
∴ 65 = 5 × 13, 117 = 32 × 13
⇒ HCF (65, 117) = 13
∴ Required greatest number = 13.
Q6: Assertion (A): For any two prime numbers p and q, their HCF is 1 and LCM is p + q.
Reason (R): For any two natural numbers, HCF x LCM = product of numbers.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true, but Reason (R) is false.
(d) Assertion (A) is false, but Reason (R) (ii) is true. (2025)
 View Answer
View Answer 
Ans: (d)
Clearly, reason is true.
For any two primes p and q.
HCF (p, q) = 1
LCM (p, q) = p × q
∴ Assertion is false.
Q7: Find the smallest number that is divisible by both 644 and 462. (2025)
 View Answer
View Answer 
Ans:
The smallest number divisible by both 644 and 462 is LCM of 644 and 462.
644 = 2 × 2 × 7 × 23
462 = 2 × 3 × 7 × 11
∴ LCM (644,462) = 2 × 2 × 3 × 7 × 11 × 23 = 21252
Q8: Two numbers are in the ratio 4: 5 and their HCF is 11. Find the LCM of these numbers. (2025)
 View Answer
View Answer 
HCF (4x, 5x) = 11
∴ Numbers are 4 × 11 = 44 and 5 × 11 = 55
Since, product of two numbers= HCF × LCM
⇒ 44 × 55 = 11 × LCM

Q9: Three sets of Physics, Chemistry and Mathematics books have to be stacked in such a way that all the books are stored subject-wise and the height of each stack is the same. The number of Physics books is 144, the number of Chemistry books is 180 and the number of Mathematics books is 192. Assuming that the books are of same thickness,determine the number of stacks of Physics, Chemistry and Mathematics books. (2025)
 View Answer
View Answer 
Ans:
Number of Physics books = 144
Number of Chemistry books = 180
Number of Mathematics books = 192
Since, 180 = 2 × 2 × 3 × 3 × 5
144 = 2 × 2 × 2 × 2 × 3 × 3
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
∴ HCF(180, 144, 192) = 2 x 2 x 3 = 12
∴ Number of stacks of Physics books = 144/12 = 12
Number of stacks of Chemistry books = 180/12 = 15
Number of stacks of Mathematics books = 192/12 = 16
Q10: Let p, q and r be three distinct prime numbers.
Check whether p·q·r + q is a composite number or not.
Further, give an example for 3 distinct primes p, q, r such that
(i) p·q·r + 1 is a composite number.
(ii) p·q·r + 1 is a prime number. (2025)
 View Answer
View Answer 
Ans:
Given: p, q, r be distinct prime numbers.
We have, pqr + q = q(pr + 1)
Here, q is a prime number and pr+ 1 > 1,
Thus, pqr + q has factors 1, q, (pr+ 1) and q(pr + 1).
Hence, pqr + q is a composite number. ...(i)
(i) Take p = 3, q = 5 and r = 7, we have
pqr + 1 = 3 × 5 × 7 + 1 = 105 + 1 = 106
Thus, pqr + 1 is a composite number for p = 3, q = 5 and r = 7.
(ii) Take p = 2, q = 3 and r = 5, we have
pqr + 1 = 2 × 3 × 5 + 1 = 30 + 1 = 31
Thus, pqr + 1 is a prime number for p = 2, q = 3 and r = 5.
Q11: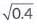 is a/an (2025)
is a/an (2025)
(a) natural number
(b) integer
(c) rational number
(d) irrational number
 View Answer
View Answer 
Ans: (d)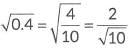
∵ 2 is a rational number and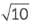 is an irrational number.
is an irrational number.
∴ 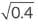 is an irrational number.
is an irrational number.
Q12: Which of the following is a rational number between √3 and √5? (2025)
(a) 1.4142387954012. ...
(b) 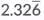
(c) π
(d) 1.857142
 View Answer
View Answer 
Ans: (d)
√3 is approximately equals to 1.7320.
√5 is approximately equals to 2.2360.
Here 1.857142 lies between √3 and √5.
Q13: Prove that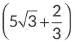 is an irrational number given that √3 is an irrational number. (2025)
is an irrational number given that √3 is an irrational number. (2025)
 View Answer
View Answer 
Ans: It is given that, √3 is an irrational number.
We have to prove that 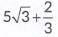 is an irrational number. 3
is an irrational number. 3
Let us assume 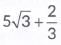 be a rational number.
be a rational number.
Then, 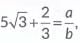 where b ≠ 0 and a, b are co-prime integers.
where b ≠ 0 and a, b are co-prime integers.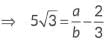
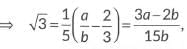 which is a rational number.
which is a rational number.
⇒ √3 is a rational number.
But √3 is an irrational number. So, our assumption is wrong.
Hence, 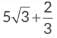 is an irrational number.
is an irrational number.
Q14: Prove that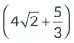 is an irrational number given that √2 is an irrational number. (2025)
is an irrational number given that √2 is an irrational number. (2025)
 View Answer
View Answer 
Ans:
It is given that, √2 is an irrational number.
We have to prove that 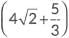 is an irrational number.
is an irrational number.
Let us assume 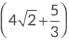 be a rational number.
be a rational number.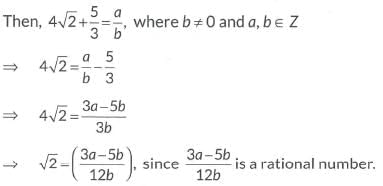
⇒√2 is a rational number.
But √2 is an irrational number. So, our assumption is wrong.
Hence,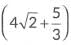 is an irrational number.
is an irrational number.
Previous Year Questions 2024
Q1: The smallest irrational number by which √20 should be multipled so as to get a rational number, is: (CBSE 2024)(a) √20
(b) √2
(c) 5
(d) √5
 View Answer
View Answer 
Ans: (d)

Q2: The LCM of two prime numbers p and q (p > q) is 221. Then the value of 3p – q is: (CBSE 2024)
(a) 4
(b) 28
(c) 38
(d) 48
 View Answer
View Answer 
Ans: (c)
The numbers p and q are prime numbers,
∴ HCF (p, q) = 1
Here, LCM(p, q) = 221
∴ As, p > q
p = 17, q = 13
(As p × q = 221)
Now, 3p – q = 3 × 17 – 13
= 51 – 13
= 38
Q3: A pair of irrational numbers whose product is a rational number is (CBSE 2024)
(a) (√16, √4)
(b) (√5, √2)
(c) (√3, √27)
(d) (√36, √2)
 View Answer
View Answer 
Ans:(c)
Here √3 and √27 both are irrational numbers.
The product of √3 x √27 = √3 x 27
= √81
= 9 ,= pq;q ≠ 0
∴ 9 is a rational number.
Q4: Given HCF (2520, 6600) = 40, LCM (2520, 6600) = 252 × k, then the value of k is: (CBSE 2024)
(a) 1650
(b) 1600
(c) 165
(d) 1625
 View Answer
View Answer 
Ans:(a)
HCF(2520, 6600) = 40
LCM(2520, 6600) = 252 × k
∴ HCF × LCM = Ist No. × IInd No.
∴ 40 × 252 × k = 2520 × 6600
⇒ k = 2520 x 660040 x 252
⇒ k = 1650
Q5: Teaching Mathematics through activities is a powerful approach that enhances students' understanding and engagement. Keeping this in mind, Ms. Mukta planned a prime number game for class 5 students. She announced the number 2 in her class and asked the first student to multiply it by a prime number and then pass it to the second student. The second student also multiplied it by a prime number and passed it to the third student. In this way by multiplying by a prime number, the last student got 173250.
Now, Mukta asked some questions as given below to the students: (CBSE 2024)
(A) What is the least prime number used by students?
(B) How many students are in the class?
OR
What is the highest prime number used by students?
(C) Which prime number has been used maximum times?
 View Answer
View Answer 
Ans:
(A)
So least prime no. used by students = 3(because 2 is announced by the teacher, so the least number used by the students is 3)
(B)As the last student got 173250 = 2 × 3 × 3 × 5 × 5 × 5 × 7 × 11
there are 7 factors other than 2, which is announced by teacher. So, Number of student = 7
OR
Highest prime number used by student = 11
(C)Prime number 5 is used maximum times i.e., 3 times.
Q6: LCM (850, 500) is: (CBSE 2024)
(a) 850 × 50
(b) 17 x 500
(c) 17 x 52 x 22
(d) 17 × 53 × 2
 View Answer
View Answer 
Ans: (b) 17 x 500 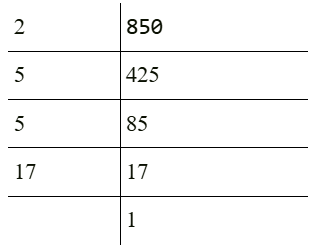
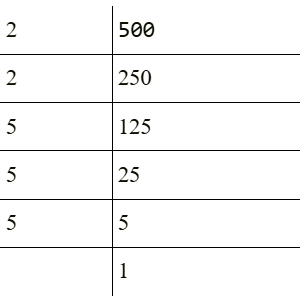
850 = 17 × 52 × 2
500 = 53 × 22
LCM (850, 500) = 17 × 53 × 22
= 17 × 500
=8500
Q7: Prove that 6 - 4√5 is an irrational number, given that √5 is an irrational number. (CBSE 2024)
 View Answer
View Answer 
Ans: Let us assume that 6 - 4√5 be a rational number
Let 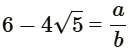 ...[b ≠ 0; a and b are integers]
...[b ≠ 0; a and b are integers]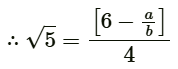
We know that, is a rational number.
is a rational number.
But this contradicts the fact that √5 is an irrational number.
So, our assumption is wrong.
Therefore, 6 - 4√5 is an irrational number.
Q8: Show that 11 × 19 × 23 + 3 × 11 is not a prime number. (CBSE 2024)
 View Answer
View Answer 
Ans: We have
11 × 19 × 23 + 3 × 11
⇒ 11(19 × 23 + 3)
⇒ 11(437 + 3)
⇒ 11(440)
⇒ 11(2 × 2 × 2 × 5 × 11)
⇒ 2 × 2 × 2 × 5 × 11 × 11
As it can be represented as a product of more than two primes (1 and number itself). So, it is not a prime number.
Q9: If two positive integers p and q can be expressed as p = 18 a²b¹ and q=20 a³b², where a and b are prime numbers, then LCM (p, q) is: (CBSE 2024)
(a) 2 a²b²
(b) 180 a²b²
(c) 12 a²b²
(d) 180 a³b²
 View Answer
View Answer 
Ans: (d) 180 a3b2
Given,
p = 18 a2b1 and
q = 20 a3b2
LCM (p, q) = LCM (18 a2b1, 20 a3b2)
= 180 a3b2
Q10: Prove that 5 - 2√3 is an irrational number. It is given that √3 is an irrational number. (CBSE 2024)
 View Answer
View Answer 
Ans: Assuming 5 – 2√3 to be a rational number. 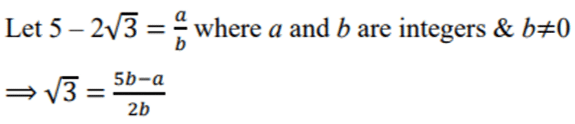
Here RHS is rational but LHS is irrational.
Therefore our assumption is wrong.
Hence, 5 – 2√3 is an irrational number.
Q11: Show that the number 5 × 11 × 17 + 3 × 11 is a composite number. (CBSE 2024)
 View Answer
View Answer 
Ans: The numbers are prime numbers and composite numbers.
Prime numbers can be divided by 1 and itself. A composite number has factors other than 1 and itself.
(5 × 11 × 17) + (3 × 11)
= (85 × 11) + (3 × 11)
= 11 × (85 + 3)
= 11 × 88
= 11 × 11 × 8
= 2 × 2 × 2 × 11 × 11
The given expression has 2 and 11 as its factors. Therefore, it is a composite number.
Q12: In a teachers' workshop, the number of teachers teaching French, Hindi and English are 48, 80 and 144 respectively. Find the minimum number of rooms required if in each room the same number of teachers are seated and all of them are of the same subject. (CBSE 2024)
 View Answer
View Answer 
Ans: The number of rooms will be minimum if each room accommodates a maximum number of teachers. Since in each room the same number of teachers are to be seated and all of them must be of the same subject. Therefore, the number of teachers in each room must be HCF of 48, 80, and 144.
The prime factorisations of 48, 80 and 144 are as under
48 = 24 × 31
80 = 24 × 51
144 = 24 × 32
∴ HCF of 48, 80 and 144 = 16
Therefore, in each room 16 teachers can be seated.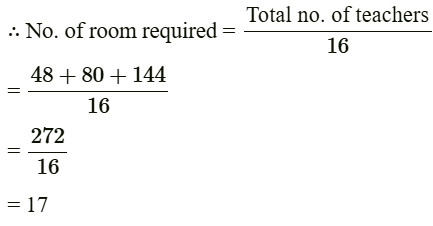
Q13: Directions: Assertion (A) is followed by a statement of Reason (R). Select the correct option from the following options:
(a) Both, Assertion (A) and Reason (R) are true. Reason (R) explains Assertion (A) completely.
(b) Both, Assertion (A) and Reason (R) are true. Reason (R) does not explain Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Assertion (A): If the graph of a polynomial touches x-axis at only one point, then the polynomial cannot be a quadratic polynomial.
Reason (R): A polynomial of degree n(n >1) can have at most n zeroes. (CBSE 2024)
 View Answer
View Answer 
Ans: Assertion (A): "If the graph of a polynomial touches the x-axis at only one point, then the polynomial cannot be a quadratic polynomial."
A quadratic polynomial is of the form ax2 + bx + c. It can have two real roots, one real root (if the discriminant is zero), or no real roots (if the discriminant is negative).
If the graph of a quadratic polynomial touches the x-axis at exactly one point, this means it has a repeated real root (a double root), which is possible for quadratic polynomials. Hence, the assertion is false.
Reason (R): "A polynomial of degree n (n > 1) can have at most n zeroes."
A polynomial of degree n can have at most n real or complex zeroes. This is a true statement, so the reason is true.
Given the above analysis, the correct answer is: (d) Assertion (A) is false but Reason (R) is true.
Previous Year Questions 2023
Q1: The ratio of HCF to LCM of the least composite number and the least prime number is (2023)(a) 1 : 2
(b) 2 : 1
(c) 1 : 1
(d) 1 : 3
 View Answer
View Answer 
Sol: Least composite number = 4
Least prime number = 2
∴ HCF = 2, LCM = 4
∴ Required ratio = HCF / LCM = 2/4
i.e. 1 : 2
Q2: Find the least number which when divided by 12, 16, and 24 leaves the remainder 7 in each case. (2023)
 View Answer
View Answer 
Ans: 55
Given, least number which when divided by 12, 16 and 24 leaves remainder 7 in each case
∴ Least number = LCM(12, 16, 24) + 7
= 48 + 7
= 55
Q3: Two numbers are in the ratio 2 : 3 and their LCM is 180. What is the HCF of these numbers? (2023)
 View Answer
View Answer 
Ans:30
Let the two numbers be 2x and 3x
LCM of 2x and 3x = 6x, HCF(2x, 3x) = x
Now, 6x = 180
⇒ x = 180/6
x = 30
Q4: Prove that √3 is an irrational number. (2023)
 View Answer
View Answer 
Ans: Let us assume that √3 is a rational number.
Then √3 = a/b; where a and b ( ≠ 0) are co-prime positive integers.
Squaring on both sides, we get
3 = a2/b2
⇒ a2 = 3b2
⇒ 3 divides a2
⇒ 3 divides a _________(i)
= a = 3c, where c is an integer
Again, squaring on both sides, we get
a2 = 9c2
⇒3b2 = 9c2
⇒b2 = 3c2
⇒ 3 divides b2
⇒ 3 divides b _________(ii)
From (i) and (ii), we get 3 divides both a and b.
⇒ a and b are not co- prime integers.
This contradicts the fact that a and b are co-primes.
Hence, √3 is an irrational number.
Previous Year Questions 2022
Q1: Two positive numbers have their HCF as 12 and their product as 6336. The number of pairs possible for the numbers is (2022)(a) 2
(b) 3
(c) 4
(d) 1
 View Answer
View Answer 
Ans:(a)
Sol: Given, HCF = 12
Let two numbers be 12a and 12b
So. 12a x 12b = 6336
⇒ ab = 44
We can write 44 as product of two numbers in these ways:
ab = 1 x 44 = 2 x 22 = 4x 11
Here, we will take a = 1 and b = 44 ; a = 4 and b = 11.
We do not take ab = 2 x 22 because 2 and 22 are not co-prime to each other.
For a = 1 and b = 44, 1st no. = 12a = 12, 2nd no. = 12b = 528
For a = 4 and b = 11, 1st no. = 12a = 48, 2nd no. = 12b = 132
Hence, we get two pairs of numbers, (12, 528) and (48, 132).
Q2: If 'n' is any natural number, then (12)n cannot end with the digit (2022)
(a) 2
(b) 4
(c) 8
(d) 0
 View Answer
View Answer 
Ans: (d)
Sol:
- For any natural number n, the expression (12)n cannot end with the digit 0.
- This is because the number 12 does not contain the prime factor 5, which is necessary for a number to end in 0.
- Thus, regardless of the value of n, (12)n will never end with 0.
Q3: The number 385 can be expressed as the product of prime factors as (2022)
(a) 5 x 11 x 13
(b) 5 x 7 x 11
(c) 5 x 7 x 13
(d) 5 x 11 x 17
 View Answer
View Answer 
Ans: (b)
Sol: We have,

∴ Prime factorisation of 385 = 5 x 7 x 11
Previous Year Questions 2021
Q1: Explain why 2 x 3 x 5 + 5 and 5 x 7 x 11 + 7 x 5 are composite numbers. (2021)
 View Answer
View Answer 
Ans: We have, 2 x 3 x 5 + 5 and 5 x 7 x 11 + 7 x 5.
We can write these numbers as:
2 x 3 x 5 + 5 = 5(2 x 3 + 1)
= 1 x 5 x 7
and 5 x 7 x 11 + 7 x 5 = 5 x 7(11 + 1)
= 5 x 7 x 12 = 1 x 5 x 7 x 12
Since, on simplifying. we find that both the numbers have more than two factors.
So. these are composite numbers.
Previous Year Questions 2020
Q1: The HCF and the LCM of 12, 21 and 15 respectively, are (2020)(a) 3, 140
(b) 12, 420
(c) 3, 420
(d) 420, 3
 View Answer
View Answer 
Ans: (c)
Sol:We have,
12 = 2 x 2 x 3 = 22 x 3
21= 3 x 7
15 = 3 x 5
∴ HCF (12, 21, 15) = 3
and LCM (12, 21 ,15 ) = 22 x 3 x 5 x 7
= 420
Q2: The LCM of two numbers is 182 and their HCF is 13. If one of the numbers is 26. find the other. (2020)
 View Answer
View Answer 
Ans: Let the other number be x
As, HCF (a, b) x LCM (a, b) = a x b
⇒ 13 x 182= 26x
⇒ x = 13 x 182 / 26
= 91
Hence, other number is 91.
Q3: Given that HCF (135, 225) = 45, find the LCM (135, 225). (CBSE 2020)
 View Answer
View Answer 
Ans: We know that
LCM × HCF = Product of two numbers
∴ LCM (135, 225) = Product of 135 and 225 / HCF(135, 225)
= 135 x 225 / 45
= 675
So, LCM (135, 225) = 675
Previous Year Questions 2019
Q1: If HCF (336, 54) = 6. find LCM (336, 54). (2019) View Answer
View Answer 
Ans: Using the formula: HCF (a, b) x LCM (a, b) = a x b
∴ HCF (336, 54) x LCM (336, 54) = 336 x 54
⇒ 6 x LCM(336, 54) = 18144
⇒ LCM (336, 54) = 18144 / 6
= 3024
Q2: The HCF of two numbers a and b is 5 and their LCM is 200. Find the product of ab. (2019)
 View Answer
View Answer 
Ans: We know that HCF (a, b) x LCM (a, b)=a x b
⇒ 5 x 200 = ab
⇒ ab = 1000
Q3: If HCF of 65 and 117 is expressible in the form 65n - 117, then find the value of n. (2019)
 View Answer
View Answer 
Ans: Since, HCF (65 ,117) = 13
Given HCF ( 65, 117 ) = 65n - 117
13 = 65n - 117
⇒ 65n = 13 +117
⇒ n = 2
Q4: Find the HCF of 612 and 1314 using prime factorization. (2019)
 View Answer
View Answer 
Ans: Prime factorisation of 612 and 1314 are
612 = 2 x 2 x 3 x 3 x 17
1314 = 2 x 3 x 3 x 73
∴ HCF (612, 1314) = 2 x 3 x 3
= 18
Q5: Prove that √5 is an irrational number. (2019)
 View Answer
View Answer 
Ans: Let us assume that √5 is a rational number.
Then √5 = a/b where a and b (≠ 0} are co-prime integers,
if Squaring on both sides, we get
5 = a2b2 ⇒ a2 = 5b2
⇒ 5 divides a2
⇒ 5 divides a ----------(i)
⇒ a = 5c, where c is an integer
Again, squaring on both sides, we get
a2 = 25c2
⇒ 5b2 = 25c2
⇒ b2 = 5c2
⇒ 5 divides b2 ----------(ii)
⇒ 5 divides b
From (i) and {ii), we get 5 divides both a and b.
⇒ a and b are not co-prime integers.
Hence, our supposition is wrong.
Thus, √5 is an irrational number.
Q6: Prove that √2 is an irrational number. (2019)
 View Answer
View Answer 
Ans: Let us assume √2 be a rational number.
Then, √2 = p/q where p, q (q ≠ 0) are integers and co-prime. ;
On squaring both sides. we get
2 = p2q2 ⇒ p2 = 2q2 ------------(i)
⇒ 2 divides p2
⇒ 2 divides p -----------(ii)
So, p = 2a, where a is some integer.
Again squaring on both sides, we get
p2 = 4a2
⇒ 2q2 = 4a2 (using (i))
⇒ q2 = 2a2
⇒ 2 divides q2
⇒ 2 divides q -----------(iii)
From (ii) and (iii), we get
2 divides both p and q.
∴ p and q are not co-prime integers.
Hence, our assumption is wrong.
Thus √2 is an irrational number.
Q7: Prove that 2 + 5√3 is an irrational number given that √3 is an irrational number. (2019)
 View Answer
View Answer 
Ans: Suppose 2 + 5√3 is a rational number.
We can find two integers a, b (b ≠ 0) such that
2 + 5√3 = a/b, where a and b are co -prime integers.
5√3 = ab - 2 ⇒ √3 = 15 [ a b - 2]
⇒ √3 is a rational number.
[ ∵ a, b are integers, so 15 [ a b - 2] is a rational number]
But this contradicts the fact that √3 is an irrational number.
Hence, our assumption is wrong.
Thus, 2 + 5√3 is an irrational number.
Q8: Write the smallest number which is divisible by both 306 and 657. (CBSE 2019)
 View Answer
View Answer 
Ans: Given numbers are 306 and 657.
The smallest number divisible by 306 and 657 = LCM(306, 657)
Prime factors of 306 = 2 × 3 × 3 × 17
Prime factors of 657 = 3 × 3 × 73
LCM of (306, 657) = 2 × 3 × 3 × 17 × 73
= 22338
Hence, the smallest number divisible by 306 and 657 is 22,338.
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 1 Previous Year Questions - Real Numbers
| 1. What are the key concepts covered in the CBSE Real Numbers chapter? |  |
| 2. How can I prepare effectively for Real Numbers in the CBSE exams? |  |
| 3. What type of questions are commonly asked from the Real Numbers chapter in CBSE exams? |  |
| 4. Are there any important formulas or theorems related to Real Numbers that I should remember for the exam? |  |
| 5. How are Real Numbers relevant in everyday life and other subjects? |  |






















