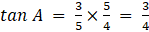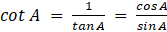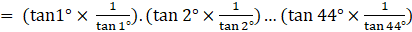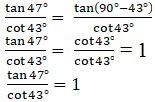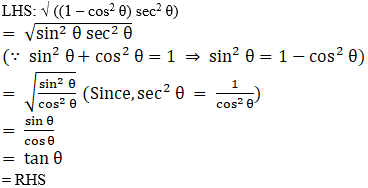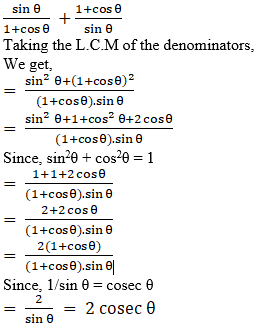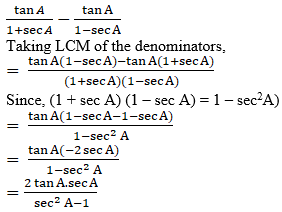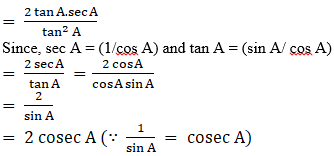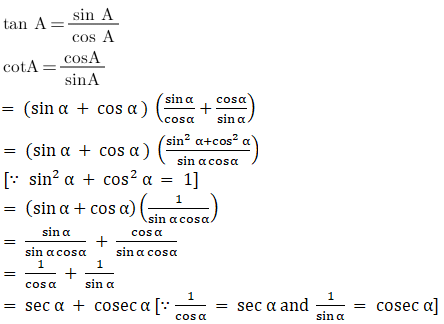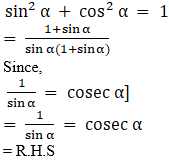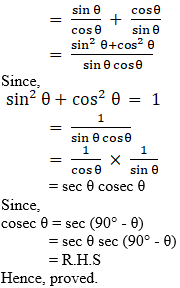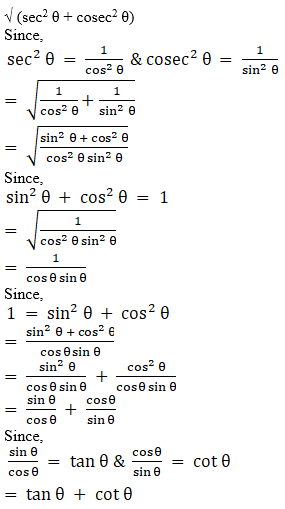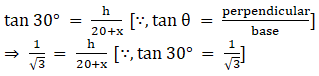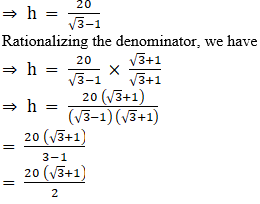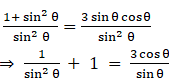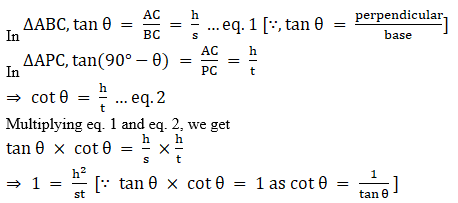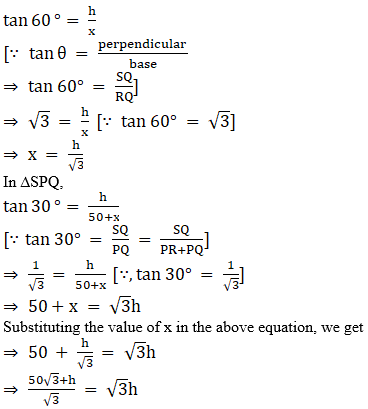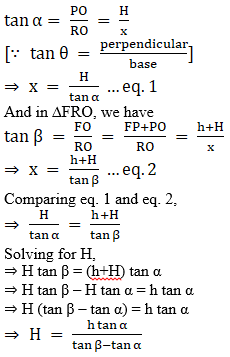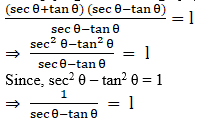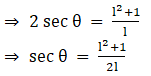NCERT Exemplar: Introduction to Trigonometry | Mathematics (Maths) Class 10 PDF Download
Exercise 8.1
Choose the correct answer from the given four options:
Q.1. If cos A = 4/5, then the value of tan A is
(a) 3/5
(b) 3/4
(c) 4/3
(d) 5/3
Correct Answer is option (b)
According to the question,
cos A = 4/5 …(1)
We know,
tan A = sinA/cosA
To find the value of sin A,
We have the equation,
sin2 θ +cos2 θ = 1
So, sin θ = √ (1-cos2 θ)
Then,
sin A = √ (1-cos2 A) …(2)
sin2 A = 1-cos2 A
sin A = √(1-cos2 A)
Substituting equation (1) in (2),
We get,
Sin A = √(1-(4/5)2)
= √(1-(16/25))
= √(9/25)
= 3/5
Therefore,
Q.2. If sin A = 1/2, then the value of cot A is
(a) √3
(b) 1/√3
(c) √3/2
(d) 1
Correct Answer is option (a)
(A) √3
According to the question,
Sin A = ½ … (1)
We know that,
To find the value of cos A.
We have the equation,
sin2 θ +cos2 θ =1
So, cos θ = √(1-sin2 θ)
Then,
cos A = √(1-sin2 A) … (3)
cos2 A = 1-sin2 A
cos A = √ (1 - sin2 A)
Substituting equation 1 in 3, we get,
cos A = √(1 - 1/4) = √(3/4) = √3/2
Substituting values of sin A and cos A in equation 2, we get
cot A = (√3/2) × 2 = √3
Q.3. The value of the expression [cosec (75° + θ) – sec (15° – θ) – tan (55° + θ) + cot (35° – θ)] is
(a) – 1
(b) 0
(c) 1
(d) 3 2
Correct Answer is option (b)
According to the question,
We have to find the value of the equation,
cosec(75° + θ) – sec(15° - θ) – tan(55° + θ) + cot(35° - θ)
= cosec[90°-(15°-θ)] – sec(15°-θ) – tan(55°+θ) + cot[90°-(55°+θ)]
Since, cosec (90°- θ) = sec θ
And, cot(90°-θ) = tan θ
We get,
= sec(15° - θ) – sec(15° - θ) – tan(55° + θ) + tan(55° + θ)
= 0
Q.4. Given that sinθ = a b , then cosθ is equal to
(a) b/√(b2 – a2)
(b) b/a
(c) √(b2 - a2)/b
(d) a/√(b2 - a2)
Correct Answer is option (c)
According to the question,
sin θ = a/b
We know, sin2 θ +cos2 θ = 1
sin2 A = 1 - cos2 A
sin A = √(1-cos2 A
So, cos θ = √(1 - a2/b2 ) = √((b2 - a2)/b2 ) = √(b2 - a2 )/b
Hence, cos θ = √(b2 – a2 )/b
Q.5. If cos (α + β) = 0, then sin (α – β) can be reduced to
(a) cos β
(b) cos 2β
(c) sin α
(d) sin 2α
Correct Answer is option (b)
According to the question,
cos(α+β) = 0
Since, cos 90° = 0
We can write,
cos(α+β)= cos 90°
By comparing cosine equation on L.H.S and R.H.S,
We get,
(α + β) = 90°
α = 90°- β
Now we need to reduce sin (α - β),
So, we take,
sin(α - β) = sin(90°- β - β) = sin(90°- 2β)
sin(90° - θ) = cos θ
So, sin(90° - 2β) = cos 2β
Therefore, sin(α - β) = cos 2β
Q.6. The value of (tan1° tan2° tan3° … tan89°) is
(a) 0
(b) 1
(c) 2
(d) 1/2
Correct Answer is option (b)
tan 1°. tan 2°.tan 3° …… tan 89°
= tan1°.tan 2°.tan 3°…tan 43°.tan 44°.tan 45°.tan 46°.tan 47°…tan 87°.tan 88°.tan 89°
Since, tan 45° = 1,
= tan1°.tan 2°.tan 3°…tan 43°.tan 44°.1.tan 46°.tan 47°…tan 87°.tan 88°.tan 89°
= tan1°.tan 2°.tan 3°…tan 43°.tan 44°.1.tan(90°-44°).tan(90°-43°)…tan(90°-3°). tan(90°-2°).tan(90°-1°)
Since, tan(90°-θ) = cot θ,
= tan1°.tan 2°.tan 3°…tan 43°.tan 44°.1.cot 44°.cot 43°…cot 3°.cot 2°.cot 1°
Since, tan θ = (1/cot θ)
= tan1°.tan 2°.tan 3°…tan 43°.tan 44°.1. (1/tan 44o). (1/tan 43o)… (1/tan 3o). (1/tan 2o). (1/tan 1o)
= 1
Hence, tan 1°.tan 2°.tan 3° …… tan 89° = 1
Q.7. If cos 9α = sinα and 9α < 90°, then the value of tan5α is
(a) 1/√3
(b) √3
(c) 1
(d) 0
Correct Answer is option (c)
According to the question,
cos 9∝ = sin ∝ and 9∝<90°
i.e. 9α is an acute angle
We know that,
sin(90°-θ) = cos θ
So,
cos 9∝ = sin (90°- ∝)
Since, cos 9∝ = sin(90°- 9∝) and sin(90°- ∝) = sin∝
Thus, sin (90°- 9∝) = sin∝
90°- 9∝ = ∝
10∝ = 90°
∝ = 9°
Substituting ∝ = 9° in tan 5∝, we get,
tan 5∝ = tan (5 × 9) = tan 45° = 1
∴, tan 5∝ = 1
Q.8. If ∆ABC is right angled at C, then the value of cos (A + B) is
(a) 0
(b) 1
(c) 1/2
(d) √3/2
Correct Answer is option (a)
Given, the triangle ABC is a right triangle with C at right angle.
We have to find the value of cos(A + B)We know that the sum of all the three interior angles of a triangle is always equal to 180°
So, ∠A + ∠B + ∠C = 180°
∠A + ∠B + 90° = 180°
∠A + ∠B = 180° - 90°
∠A + ∠B = 90°
So, cos (A+B) = cos 90°
Using the trigonometric ratios of angles,
cos 90° = 0
Therefore, the value of cos(A + B) is zero.
Q.9. If sinA + sin2 A = 1, then the value of the expression (cos2 A + cos4 A) is
(a) 1
(b) 1/2
(c) 2
(d) 3
Correct Answer is option (a)
Given, sinA + sin2 A = 1
It can be written as
sin A = 1 - sin2 A …. (1)
We have to find the value of (cos2 A + cos4 A)
Using the trigonometric identities,
cos2 A = 1 - sin2 A ….. (2)
From both the equations
sin A = cos2 A
Now, (cos2 A + cos4 A) = (cos2A + (sin A)2)
= cos2A + sin2A
Using the trigonometric identities,
cos2 A + sin2 A = 1
Therefore, (cos2 A + cos4 A) = 1
Q.10. Given that sinα = 1/2 and cosβ = 1/2, then the value of (α + β) is
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Correct Answer is option (d)
Given, sinα = 1/2 and cosβ = 1/2
We have to find the value of (α + β)
Using the trigonometric ratios of angles,
Given, sinα = 1/2
α = sin⁻¹(1/2)
α = 30°
Given, cosβ = 1/2
β = cos⁻¹(1/2)
β = 60°
Now, (α + β) = 30° + 60°
= 90°
Therefore, the value of (α + β) = 90°
Q.11. The value of the expression [(sin222°+sin268°)/(cos222°+cos268°)] +sin263° +cos 63°sin 27°
(a) 3
(b) 2
(c) 1
(d) 4
Correct Answer is option (b)
We have to find the value of the expression [(sin²22°+sin²68°)/(cos²22°+cos²68°)] + sin²63° +cos63°sin27°
Using the trigonometric ratio of complementary angles,
sin (90° - A) = cos A
sin²68° = sin²(90° - 22°) = cos²22°
So, sin²68° = cos²22°
Now, sin²22° + sin²68° can be written as
= sin²22° + cos²22°
By using the trigonometric identities,
cos² A + sin² A = 1
So, sin²22° + cos²22° = 1
Using the trigonometric ratio of complementary angles,
cos (90° - A) = sin A
cos²22° = cos²(90°- 68°) = sin²68°
cos²22° + cos²68° can be written as
= sin²68° + cos²68°
= 1
So, (sin²22° + sin²68°)/(cos²22° + cos²68°) = 1/1 = 1
Now, cos63°sin27° can be simplified a
= cos 63° sin (90° - 63°)
= cos 63° cos 63°
= cos²63°
Now, sin²63° + cos63°sin27° can be written as
= sin²63° + cos²63°
= 1
[(sin²22°+ sin²68°)/(cos²22°+ cos²68°)] + sin²63° + cos63°sin27° = 1 + 1 = 2
Therefore, the value of the expression is 2.
Q.12. If 4 tanθ = 3, then (4sinθ − cosθ)/(4sinθ + cosθ) is equal to
(a) 2/3
(b) 1/3
(c) 1/2
(d) 3/4
Correct Answer is option (c)
Given, 4 tanθ = 3
We have to find the value of (4sinθ - cosθ)/(4sinθ + cosθ)
Now, tanθ = 3/4
We know that tan A = opposite / adjacent
Opposite = 3
Adjacent = 4
Using the pythagorean theorem,
(hypotenuse)² = (opposite)² + (adjacent)²
(hypotenuse)² = (3)² + (4)²
(hypotenuse)² = 9 + 16
(hypotenuse)² = 25
Taking square root,
Hypotenuse = 5
We know that sin A = opposite/hypotenuse
So, sinθ = 3/5
We know that cos A = adjacent / hypotenuse
So, cosθ = 4/5
Now, (4sinθ - cosθ) = 4(3/5) - (4/5)
= 12/5 - 4/5
= (12 - 4)/5
= 8/5
Now, (4sinθ + cosθ) = 4(3/5) + (4/5)
= 12/5 + 4/5
= (12 + 4)/5
= 16/5
So, (4sinθ - cosθ)/(4sinθ + cosθ) = (8/5) / (16/5)
= 8(5) / 16(5)
= 8/16
= 1/2
Q.13. If sinθ - cosθ = 0, then the value of (sin4 θ + cos4 θ) is
(a) 1
(b) 3/4
(c) 1/2
(d) 1/4
Correct Answer is option (c)
Given, sinθ - cosθ = 0
We have to find the value of sin⁴ θ + cos⁴ θ
sinθ = cosθ
We know that sin A/cos A = tan A
sinθ/cosθ = tanθ
So, tanθ = 1
θ = tan⁻¹(1)
tan 45° = 1
So, θ = 45°
Now, sin⁴ θ = sin⁴ 45°
From the above table,
sin 45° = 1/√2
So, sin⁴ 45° = (1/√2)⁴ = 1/4
Now, cos⁴ θ = cos⁴ 45°
From the above table,
cos 45° = 1/√2
So, cos⁴ 45° = (1/√2)⁴ = 1/4
sin⁴ θ + cos⁴ θ = 1/4 + 1/4
= (1 + 1)/4
= 2/4
= 1/2
Therefore, sin⁴ θ + cos⁴ θ = 1/2.
Q.14. sin (45° + θ) - cos (45° - θ) is equal to
(a) 2cosθ
(b) 0
(c) 2sinθ
(d) 1
Correct Answer is option (b)
We have to find the value of sin (45° + θ) - cos (45° - θ)
By using the trigonometric ratios of complementary angles,
cos (90° - A) = sin A
cos (45° - θ) = cos (90° - (45° - θ))
= cos(90° - 45° + θ)
= sin(45°+ θ)
sin(45°+ θ) - cos(45°- θ) = sin(45°+ θ) - sin(45°+ θ)
= 0
Therefore, the value of the given expression is 0.
Q.15. A pole 6 m high casts a shadow 2√3 m long on the ground, then the Sun’s elevation is
(a) 90°
(b) 30°
(c) 60°
(d) 45°
Correct Answer is option (c)
Given, length of pole = 6 m
Pole casts a shadow of 2√3 m long on the ground.
We have to find the sun’s elevation.
Let θ be the angle of elevation.From the figure,
Opposite = 6 m
Adjacent = 2√3 m
tan θ = opposite/hypotenuse
tan θ = 6/2√3
tan θ = 3/√3
tan θ = √3
θ = tan⁻¹(√3)
Using the trigonometric ratios of angles,
tan 60° = √3
So, θ = 60°
Therefore, the angle of elevation is 60°
Exercise 8.2
Write ‘True’ or ‘False’ and justify your answer in each of the following:
Q.1. tan 47o/cot 43° = 1
True
Justification:
Since, tan (90° - θ) = cot θ
Q.2. The value of the expression (cos223° – sin267°) is positive.
Solution:
False
Justification:
Since, (a2 - b2) = (a + b)(a - b)
cos2 23° – sin2 67° =(cos 23°+sin 67°)(cos 23°-sin 67°)
= [cos 23°+sin(90°-23°)] [cos 23°-sin(90°-23°)]
= (cos 23°+cos 23°)(cos 23°-cos 23°) (∵sin(90°-θ) = cos θ)
= (cos 23°+cos 23°).0
= 0, which is neither positive nor negative
Q.3. The value of the expression (sin 80° – cos 80°) is negative.
False
Justification:
We know that,
sin θ increases when 0° ≤ θ ≤ 90°
cos θ decreases when 0° ≤ θ ≤ 90°
And (sin 80°-cos 80°) = (increasing value-decreasing value)
= a positive value.
Therefore, (sin 80°-cos 80°) > 0.
Q.4. √((1– cos2θ) sec2 θ)= tan θ
True
Justification:
Q.5. If cosA + cos2A = 1, then sin2A + sin4A = 1.
True
Justification:
According to the question,
cos A+cos2 A = 1
i.e., cos A = 1- cos2 A
Since,
sin2 θ+cos2 θ = 1
sin2 θ = 1- cos2 θ)
We get,
cos A = sin2 A …(1)
Squaring L.H.S and R.H.S,
cos2 A = sin4 A …(2)
To find sin2A+sin4 A = 1
Adding equations (1) and (2),
We get
sin2A + sin4 A= cos A + cos2 A
Therefore, sin2A + sin4 A = 1
Q.6. (tan θ + 2) (2 tan θ + 1) = 5 tan θ + sec2 θ.
False
Justification:
L.H.S = (tan θ + 2) (2 tan θ + 1)
= 2 tan2 θ + tan θ + 4 tan θ + 2
= 2 tan2θ + 5 tan θ + 2
Since, sec2 θ – tan2 θ = 1, we get, tan2θ = sec2 θ - 1
= 2(sec2 θ-1) +5 tan θ + 2
= 2 sec2 θ - 2 + 5 tan θ + 2
= 5 tan θ + 2 sec2 θ ≠ R.H.S
∴, L.H.S ≠ R.H.S
Q.7. If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing. Write ‘True’ or ‘False’ and justify your answer.
Consider a pole of height 2√3 m cast a shadow of 2 m, then the sun’s elevation is θ
By pythagorean theorem,
tan θ = opposite/adjacent
tan θ = 2√3/2
tan θ = √3
θ = tan⁻¹(√3)
We know that tan 60° = √
So, θ = 60°
Now, shadow increases to 4 m, then the angle of elevation is θtan θ = 2√3/(2 + 4)
tan θ = 2√3/6
tan θ = √3/3
tan θ = 1/√3
θ = tan⁻¹(1/√3)
We know that tan 30° = 1/√3
So, θ = 30°
It is clear from the two cases that the angle of elevation decreases when the length of the shadow increases.
False. Longer shadow ⇒ smaller angle
Q.8. If a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection. Write ‘True’ or ‘False’ and justify your answer.
False
Given, a man standing on a platform 3 metres above the surface of a lake observes a cloud and its reflection in the lake.
We have to determine if the angle of elevation of the cloud is equal to the angle of depression of its reflection.Let M be the position where a man is standing on a platform.
C is the cloud
MO is the height of the platform from the surface of the lake.
MO = 3 m
Let θ₁ be the angle of elevation
Let θ₂ be the angle of depression
Height of reflection of the cloud = (h + 3) m
In triangle MPC,
tan θ₁ = CM/PM
tan θ₁ = h/PM
PM = h/tan θ₁ ---- (1)
In triangle MPC’,
tan θ₂ = C’M/PM
tan θ₂ = (h + 3)/PM
PM = (h + 3)/tan θ₂ ------ (2)
From (1) and (2),
h/tanθ₁ = (h + 3)/tanθ₂
h(tanθ₂) = (h + 3) tanθ₁
So, tanθ₁ = h/(h + 3) tanθ₂
It is clear that θ₁ ≠ θ₂
Therefore, the angle of elevation is not equal to the angle of depression.
Q.9. The value of 2sinθ can be a+(1/a), where a is a positive number and a ≠ 1. Write ‘True’ or ‘False’ and justify your answer.
False
Given, a is positive number and a ≠ 1
We have to determine if 2sinθ can be a + (1/a)
Arithmetic mean of a and 1/a = a + (1/a) / 2
Geometric mean of a and 1/a = √a × (1/a) = 1
So, arithmetic mean > geometric mean
i.e., [a + (1/a)]/2 > 1
[a + (1/a)] > 2
Now, 2sinθ > 2
sinθ > 1
Therefore, 2sinθ cannot be a + (1/a)
Q.10. cos θ = (a2 + b2)/2ab, where a and b are two distinct numbers such that ab > 0. Write ‘True’ or ‘False’ and justify your answer.
Given, a and b are two distinct numbers such that ab > 0.
We have to determine if cos θ = (a² + b²)/2ab
Arithmetic mean > Geometric Mean
As AM = (a + b)/2
GM=√ab
So we get
(a² + b²)/2 > √a²b²
(a² + b²)/2 > ab
By cross multiplication
(a² + b²)/2ab > 1
It is given that
cos θ > 1
We know that the value of cos θ varies between 0 and 1.
Base/ Hypotenuse > 1
Base > Hypotenuse
As the value of cos cannot be greater than 1, the given statement is false.
Therefore, the given statement is false.
Q.11. The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled. Write ‘True’ or ‘False’ and justify your answer.
False
Given, angle of elevation of the top of a tower is 30°
We have to determine if the height of the tower is doubled, the angle of elevation of its top will also be doubled i.e., θ = 60°Let AC be the height of the tower
AC = h units
BC = x units
Angle of elevation = 30°
By pythagorean theorem,
tan 30° = AC/BC
By using trigonometric ratio of angles,
tan 30° = 1/√3
1/√3 = h/x ------------ (1)Now, the height of the tower is doubled.
So, PR = 2h units
RQ = x units
Let the angle of elevation be θ
tan θ = PR/RQ
tan θ = 2h/x ---------------- (2)
Substituting (1) in (2),
tan θ = 2(1/√3)
tan θ = 2/√3
tan θ = 1.15
θ = tan⁻¹(1.15)
θ = 49°< 60°
Therefore, the angle of elevation is not doubled.
Q.12. If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged. Write ‘True’ or ‘False’ and justify your answer.
Given, the height of the tower and the distance of the point of observation from its foot are increased by 10%.
We have to determine if the angle of elevation of its top remains unchanged.Let AB be the height of tower
Let BC be the distance of the point of observation from its foot.
Let AB = x units and BC = y units
Angle of elevation be θ
In triangle ABC,
tan θ = AB/BC
tan θ = x/y ------------------ (1)
Now, x and y are increased by 10%
x = x + (1/10)x = (1 + 10)/10 x = 11x/10
y = y + (1/10)y = (1 + 10)/10 y = 11y/10
tan θ = (11/10)x / (11/10)y
tan θ = x/y ------------------- (2)
From (1) and (2),
θ remains same
Therefore, the angle of elevation remains unchanged.
Exercise 8.3
Prove the following (from Q.1 to Q.7):
Q.1. sin θ/(1 + cos θ) + (1 + cos θ)/sin θ = 2cosec θ
L.H.S =
R.H.S
Hence proved.
Q.2. tan A/(1 + secA) – tan A/(1 - secA) = 2cosec A
L.H.S:
Since,
sec2A – tan2A = 1
sec2A – 1 = tan2A
= R.H.S
Hence proved.
Q.3. If tan A = ¾, then sinA cosA = 12/25
According to the question,
tan A = ¾
We know,
tan A = perpendicular/ base
So,
tan A = 3k/4k
Where,
Perpendicular = 3k
Base = 4kUsing Pythagoras Theorem,
(hypotenuse)2 = (perpendicular)2 + (base)2
(hypotenuse)2 = (3k)2+ (4k)2 = 9k2+16k2 = 25k2
hypotenuse = 5k
To find sin A and cos A,
Hence, proved.
Q.4. (sin α + cos α) (tan α + cot α) = sec α + cosec α
L.H.S:
(sin α + cos α) (tan α + cot α)
As we know,
= R.H.S
Hence, proved.
Q.5. (√3+1) (3 – cot 30°) = tan3 60° – 2 sin 60°
L.H.S: (√3 + 1) (3 – cot 30°)
= (√3 + 1) (3 – √3) [∵cot 30° = √3]
= (√3 + 1) √3 (√3 – 1) [∵(3 – √3) = √3 (√3 – 1)]
= ((√3)2– 1) √3 [∵ (√3+1)(√3-1) = ((√3)2 – 1)]
= (3-1) √3
= 2√3
Similarly solving R.H.S: tan3 60° – 2 sin 60°
Since, tan 60o = √3 and sin 60o = √3/2,
We get,
(√3)3 – 2.(√3/2) = 3√3 – √3
= 2√3
Therefore, L.H.S = R.H.S
Hence, proved.
Q.6. 1 + (cot2 α/1+cosec α) = cosec α
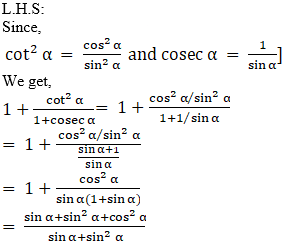
And, we know that,
Q.7. tan θ + tan (90° – θ) = sec θ sec (90° – θ)
L.H.S =
Since, tan (90° – θ) = cot θ
tan θ + tan (90° – θ)= tan θ + cot θ
Q.8. Find the angle of elevation of the sun when the shadow of a pole h metres high is √3 h metres long.
From the figure
In triangle ABC
tan θ = opposite/adjacent
tan θ = AC/BC
Substituting the values
tan θ = h/√3 h
tan θ = 1/ √3 = tan 30°
So we get
θ = 30°
Therefore, the angle of elevation is 30°.
Q.9. If √3 tan θ = 1, then find the value of sin2 θ - cos2 θ.
It is given that
√3 tan θ = 1
It can be written as
tan θ = 1/√3
By taking tan inverse
θ = tan-1 (1/√3)
θ = 30°
To determine the value of sin2 θ - cos2 θ
Let us substitute the value of θ
sin2 30° - cos2 30°
= (1/2)2 - (√3/2)2
By further simplification
= 1/4 - 3/4
So we get
= -2/4
= -1/2
Therefore, the value of sin2 θ - cos2 θ is -1/2.
Q.10. A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
Consider the length of the ladder = 15 m (Hypotenuse)
From the figure
Angle between the ladder and the wall ∠BCA = 60°
Angle between ladder and the ground ∠CAB = 90° - 60° = 30°
We know that
BC is the height of the wall
sin 30° = BC/15
1/2 = BC/15
So we get
BC = 15/2
BC = 7.5 m
Therefore, the height of the wall is 7.5 m.
Q.11. Simplify (1 + tan2 θ) (1 - sinθ) (1 + sinθ).
It is given that
(1 + tan2 θ) (1 - sinθ) (1 + sinθ)
As 1 + tan2 θ = sec2 θ
So we can write it as
= sec2 θ (1 - sinθ) (1 + sinθ)
Using the algebraic identity
a2 - b2 = (a + b) (a - b)
We get
= sec2 θ (1 - sin2 θ)
We know that
1 - sin2 θ = cos2 θ
By substituting it
= sec2 θ cos2 θ
Here cos2 θ = 1/sec2 θ
So we get
= sec2 θ . 1/sec2 θ
= 1
Therefore, by simplification we get 1.
Q.12. If 2sin2 θ - cos2 θ = 2, then find the value of θ.
It is given that
2 sin2 θ - cos2 θ = 2
As sin2 θ + cos2 θ = 1
We get cos2 θ = 1 - sin2 θ
2 sin2 θ - (1 - sin2 θ) = 2
By further simplification
2 sin2 θ - 1 + sin2 θ = 2
3 sin2 θ = 3
Divide both sides by 3
sin2 θ = 1
Taking square root on both sides
sin θ = 1
So we get
θ = sin-1 (1)
θ = 90°
Therefore, the value of θ is 90°.
Q.13. Show that [cos2 (45° + θ) + cos2 (45° - θ)]/ [tan (60° + θ) tan (30° - θ)] = 1.
Consider
LHS = [cos2 (45° + θ) + cos2 (45° - θ)]/ [tan (60° + θ) tan (30° - θ)]
We know that
cos A = sin (90° - A)
tan A = cot (90° - A)
tan A cot A = 1
By substituting it we get
= [cos2 (45° + θ) + sin2 (90°
- 45° + θ)]/ [tan (60° + θ) cot (90° - 30° + θ)]
So we get
= [cos2 (45° + θ) + sin2 (45° + θ)]/ [tan (60° + θ) cot (60° + θ)]
Here cos2 A + sin2 A = 1 and tan A cot A = 1
By substituting it
= 1/1
= 1
= RHS
Therefore, it is proved.
Q.14. An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
From the values given, the figure is
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer
We know that
tan A = Opposite side to angle A/Adjacent side
tan A = OB/BC
From the figure,
OB = 22 - 1.5 = 20.5 meters
BC = 20.5
So we get
tan A = 20.5/20.5 = 1 …….(i)
By trigonometric values
tan 45° = 1 ……..(ii)
From both the equations we get
A = 45°
Therefore, the angle of elevation is 45°.
Q.15. Show that tan4 θ + tan2 θ = sec4 θ - sec2 θ.
LHS = tan4 θ + tan2 θ
Taking out tan2 θ as common
= tan2 θ (tan2 θ + 1)
We know that
1 + tan2 θ = sec2 θ
i.e. tan2 θ = sec2 θ - 1
It can be written as
= (sec2 θ - 1) sec2 θ
So we get
= sec4 θ - sec2 θ
= RHS
Therefore, it is proved.
Exercise 8.4
Q.1. If cosecθ + cotθ = p, then prove that cosθ = (p2 – 1)/ (p2 + 1).
According to the question,
cosec θ + cot θ = p
Since,
Hence, proved.
Q.2. Prove that √(sec2 θ + cosec2 θ) = tan θ + cot θ
L.H.S =
√ (sec2 θ + cosec2 θ)
Since,
= R.H.S
Hence, proved.
Q.3. The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
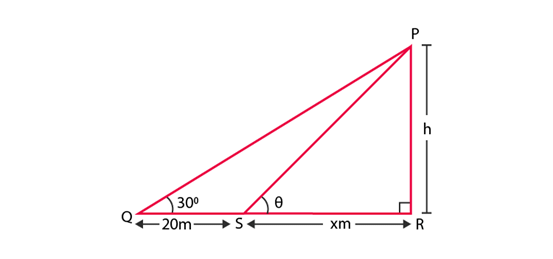
Let PR = h meter, be the height of the tower.
The observer is standing at point Q such that, the distance between the observer and tower is QR = (20 + x) m, where
QR = QS + SR = 20 + x
∠PQR = 30°
∠ PSR = θ
In ∆PQR,
Rearranging the terms,
We get 20 + x = √3h
⇒ x = √3h – 20 …eq.1
In ∆PSR,
tan θ = h/x
Since, angle of elevation increases by 15o when the observer moves 20 m towards the tower.
We have,
θ = 30° + 15° = 45°
So,
tan 45o = h/x
⇒ 1 = h/x
⇒ h = x
Substituting x=h in eq. 1, we get
h = √3 h – 20
⇒ √3 h – h = 20
⇒ h (√3 – 1) = 20
= 10 (√3 + 1)
Hence, the required height of the tower is 10 (√3 + 1) meter.
Q.4. If 1 + sin2θ = 3sinθ cosθ , then prove that tanθ = 1 or 1/2.
Given: 1+sin2 θ = 3 sin θ cos θ
Dividing L.H.S and R.H.S equations with sin2 θ,
We get,
cosec2 θ + 1 = 3 cot θ
Since,
cosec2 θ – cot2 θ = 1 ⇒ cosec2 θ = cot2 θ + 1
⇒ cot2 θ + 1 + 1 = 3 cot θ
⇒ cot2 θ +2 = 3 cot θ
⇒ cot2 θ –3 cot θ +2 = 0
Splitting the middle term and then solving the equation,
⇒ cot2 θ – cot θ –2 cot θ +2 = 0
⇒ cot θ(cot θ -1)–2(cot θ +1) = 0
⇒ (cot θ – 1)(cot θ – 2) = 0
⇒ cot θ = 1, 2
Since,
tan θ = 1/cot θ
tan θ = 1, ½
Hence, proved.
Q.5. Given that sinθ + 2cosθ = 1, then prove that 2sinθ – cosθ = 2.
Given: sin θ + 2 cos θ = 1
Squaring on both sides,
(sin θ +2 cos θ)2 = 1
⇒ sin2 θ + 4 cos2 θ + 4sin θcos θ = 1
Since, sin2 θ = 1 – cos2 θ and cos2 θ = 1 – sin2 θ
⇒ (1 – cos2 θ) + 4(1 – sin2 θ) + 4sin θcos θ = 1
⇒ 1 – cos2 θ + 4 – 4 sin2 θ + 4sin θcos θ = 1
⇒ – 4 sin2 θ – cos2 θ + 4sin θcos θ = – 4
⇒ 4 sin2 θ + cos2 θ – 4sin θcos θ = 4
We know that,
a2+ b2 – 2ab = ( a – b)2
So, we get,
(2sin θ – cos θ)2 = 4
⇒ 2sin θ – cos θ = 2
Hence proved.
Q.6. The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is √st .
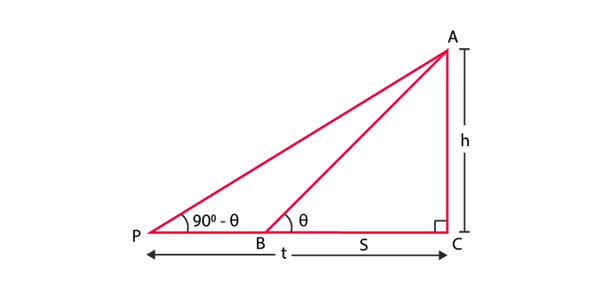
Let BC = s; PC = t
Let height of the tower be AB = h.
∠ABC = θ and ∠APC = 90° – θ
(∵ the angle of elevation of the top of the tower from two points P and B are complementary)
⇒ h2 = st
⇒ h = √st
Hence the height of the tower is √st.
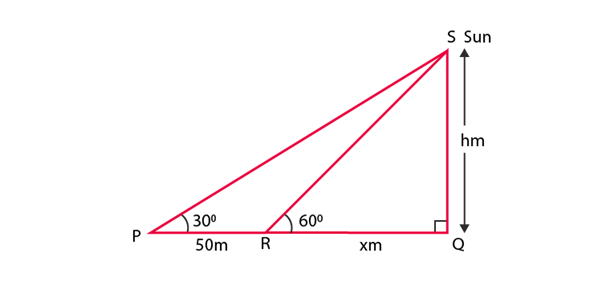
Q.7. The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
Solution:
Let SQ = h be the tower.
∠SPQ = 30° and ∠SRQ = 60°
According to the question, the length of shadow is 50 m long hen angle of elevation of the sun is 30° than when it was 60°. So,
PR = 50 m and RQ = x m
⇒ 50√3+h = 3h
⇒ 50√3 = 3h – h
⇒ 3h – h = 50√3
⇒ 2h = 50√3
⇒ h = (50√3)/2
⇒ h = 25√3
Hence, the required height is 25√3 m.
Q.8. A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is [h tan α/(tan β – tan α)].
Given that a vertical flag staff of height h is surmounted on a vertical tower of height H(say),
such that FP = h and FO = H.
The angle of elevation of the bottom and top of the flag staff on the plane is ∠PRO = α and ∠FRO = β respectivelyIn ∆PRO, we have
Hence, proved.
Q.9. If tanθ + secθ = l, then prove that secθ = (l2 + 1)/2l.
Given: tan θ+ sec θ = l …eq. 1
Multiplying and dividing by (sec θ – tan θ) on numerator and denominator of L.H.S,
So, sec θ – tan θ = 1 …eq.2
Adding eq. 1and eq. 2, we get
(tan θ + sec θ) + (sec θ – tan θ) = 1
Hence, proved.
Q.10. If sinθ + cosθ = p and secθ + cosecθ = q, then prove that q (p2 - 1) = 2p.
Given, sinθ + cosθ = p and secθ + cosecθ = q
We have to prove that q (p² - 1) = 2p.
Considering LHS: q (p² - 1)
Substituting the value of p and q,
(secθ + cosecθ)[(sinθ + cosθ)² - 1]
By using algebraic identity,
(a + b)² = a² + 2ab + b²
(sinθ + cosθ)² = sin²θ + 2sinθ cosθ + cos²θ
By using trigonometric identity,
cos² A + sin² A = 1
So, sin²θ + 2sinθ cosθ + cos²θ = 1 + 2sinθ cosθ
Now, [(sinθ + cosθ)² - 1] = 1 + 2sinθ cosθ - 1
= 2sinθ cosθ
Now, (secθ + cosecθ)[(sinθ + cosθ)² - 1] = (secθ + cosecθ)(2sinθ cosθ)
We know that sec A = 1/cos A and cosec A = 1/sin A
= (1/cosθ + 1/sinθ)(2sinθ cosθ)
On simplification,
= [(sinθ + cosθ)/sinθ cosθ](2sinθ cosθ)
= 2(sinθ + cosθ)
= 2p
= RHS
LHS = RHS
Therefore, q (p² - 1) = 2p.
Q.11. If a sinθ + b cosθ = c, then prove that a cosθ - b sinθ = √(a2 + b2 - c2).
Given, a sinθ + b cosθ = c
We have to prove that a cosθ - b sinθ = √(a² + b² - c²)
On squaring both sides,
(a sinθ + b cosθ)² = c²
By using algebraic identity,
(x + y)² = x² + 2xy + y²
Now, (a sinθ + b cosθ)² = a²sin²θ + 2absinθ cosθ + b²cos²θ
So, a²sin²θ + 2absinθ cosθ + b²cos²θ = c²
By using trigonometric identities,
cos² A + sin² A = 1
sin² A = 1 - cos² A
cos² A = 1 - sin² A
Now, a²(1 - cos² θ) + 2absinθ cosθ + b²(1 - sin² θ) = c²
a² - a²cos²θ + 2absinθ cosθ + b² - b²sin²θ = c²
a² + b² - c² = a²cos²θ - 2absinθ cosθ + b²sin²θ ---------- (1)
By using algebraic identity,
(x - y)² = x² - 2xy + y² --------- (2)
By comparing (1) and (2),
x² = a²cos²θ
x = acosθ
y² = b²sin²θ
y = bsinθ
So, a²cos²θ - 2absinθ cosθ + b²sin²θ = (acosθ - bsinθ)²
Now, (acosθ - bsinθ)² = a² + b² - c²
Taking square root,
acosθ - bsinθ = √(a² + b² - c²)
Q.12. Prove that (1+secθ-tanθ)/(1+secθ+tanθ) = (1-sinθ)/cosθ.
We have to prove that (1 + secθ - tanθ)/(1 + secθ + tanθ) = (1 - sinθ)/cosθ
Considering LHS,
LHS : (1 + secθ - tanθ)/(1 + secθ + tanθ)
By using trigonometric identity,
sec² A - tan² A = 1
(1 + secθ - tanθ) = secθ - tanθ + (sec²θ - tan²θ)
= (secθ - tanθ) + [(secθ - tanθ)(secθ + tanθ)]
Taking out common term,
= (secθ - tanθ)[1 + secθ + tanθ]
Now, (1 + secθ - tanθ)/(1 + secθ + tanθ) = (secθ - tanθ)[1 + secθ + tanθ] / (1 + secθ + tanθ)
= (secθ - tanθ)
We know that sec A = 1/cos A and tan A = sin A/cos A
So, (secθ - tanθ) = (1/cosθ - sinθ/cosθ)
= (1 - sinθ)/cosθ
= RHS
LHS = RHS
Therefore, (1 + secθ - tanθ)/(1 + secθ + tanθ) = (1 - sinθ)/cosθ
Q.13. The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
Given, the angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60°
The angle of elevation of the top of the second tower from the foot of the first tower is 30°
We have to find the distance between the two towers and also the height of the other tower.Let BQ be the first tower with height 30 m
Angle of elevation, ∠QAB = 60°
Let PA be the second tower with height h m
Angle of elevation, ∠PBA = 30°
AB is the distance between the two towers.
In triangle AQB,
By pythagorean theorem,
tan 60° = QB/AB
By trigonometric ratio of angles,
tan 60° = √3
So, √3 = 30/AB
AB = 30/√3 m
AB = 3(10)/√3
AB = 10√3 m
Therefore, the distance between two towers is 10√3 m.
In triangle APB,
By using pythagorean theorem,
tan 30° = AP/AB
By trigonometric ratio of angles,
tan 30° = 1/√3
So, 1/√3 = AP/(30/√3)
AP = (30/√3)/√3
AP = 30/3
AP = 10 m
Therefore, the height of the second tower is 10 m.
Q.14. From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
Given, from the top of a tower h m high, the angles of depression of two objects which are in line with the foot of the tower are α and β (β > α)
We have to find the distance between the two objects.Let AB be the tower
The height of the tower = h m
Angle of depression, ∠ABD = α
Angle of depression, ∠ACD = β.
Let us consider,
BC = x
CD = y
By the properties of a triangle, we know that alternate angles of a triangle are equal.
So, ∠ABD = ∠BAX = α
∠ACD = ∠CAY = β.
Considering triangle ABD,we get
tanα = AD/BD
tanα = h/BC + CD
tanα = h/x+y
y = h/tanα - x --------(1)
Considering triangle ACD,we get
tanβ = AD/CD
tanβ = h/y
y = h/tanβ --------------(2)
Now, by comparing (1) and (2), we get,
h/tanα - x = h/tanβ
x = h/tanα - h/tanβ
x = h(1/tanα - 1/tanβ)
x = h(cotα - cotβ)
Therefore, the required distance is h(cotα - cotβ).
Q.15. A ladder rests against a vertical wall at an inclination α to the horizontal. Its foot is pulled away from the wall through a distance p so that its upper end slides a distance q down the wall and then the ladder makes an angle β to the horizontal. Show that p/q = cosβ - cosα/ sinα - sinβ.
Given, a ladder rests against a vertical wall at an inclination α to the horizontal.
Its foot is pulled away from the wall through a distance p so that its upper end slides a distance q down the wall and then the ladder makes an angle β to the horizontal.
We have to prove that p/q = cosβ - cosα/ sinα - sinβ.Let AB be the ladder resting against a vertical wall
Angle of inclination, ∠BAO = α
When the foot of the ladder is pulled away through a distance p, the upper end of the ladder slides a distance q down the wall.
After sliding, SQ is the ladder
The pulled away distance, SA = p
Distance slide down the wall, BQ = q
Angle of inclination, ∠QSO = β
Let us consider,
QO = x
AO = y
Now, height of the wall,BO = q + x
Considering triangle BAO, we get
cosα = OA/AB
cosα = y/AB
y = ABcosα
Also, OA = AB cosα --------------- (1)
sin𝛼 = OB/AB
OB = BA sinα ----------------------- (2)
Considering triangle QSO, we get,
sinβ = QO/SQ
QO = SQ sinβ
cosβ = SO/SQ
SO = SQcosβ
Since the length of the ladder remains the same, we have,
AB = SQ
Hence,
QO = AB sinβ ---------------------- (3)
SO = AB cosβ ---------------------- (4)
We know that,
SA = OS - AO
p = AB cosβ - AB cosα
p = AB ( cosβ - cosα) ------------------- (5)
BQ = BO - QO
q = BA sinα - AB sinβ
q = BA (sinα - sinβ) ----------------------- (6)
According to the question, we need to prove that p/q = cosβ - cosα/ sinα - sinβ.
p/q = AB ( cosβ - cosα)/BA (sin𝛼 - sinβ)
p/q = (cosβ - cosα)/ (sinα - sinβ)
Therefore, p/q = (cosβ - cosα)/ (sinα - sinβ)
Q.16. The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
Given, the angle of elevation of the top of a vertical tower from a point on the ground is 60°
From another point vertically above the first, the angle of elevation is 45𝆩
We have to find the height of the tower.Let AP be the vertical tower.
Height of the vertical tower, AP = 10m
Angle of elevation, ∠TPO = 60𝆩
Angle of elevation of another point, ∠TAB = 45𝆩
From the above diagram,
OB = AP = 10m
Let us consider,
Distance from the point of observation to the foot of the tower, PO = x m
Total height of the tower, TO = h m
From the figure, TB = (h - 10)m
Considering the ∠TPO, we get,
tan60𝆩 = TO/PO
Since, tan60° = √3
√3 = h/x
x = h/√3--------------(1)
Considering the ∠TAB, we get,
tan45° = TH/AB
tan45° = TO - TH/AB
Since, tan45° = 1,
1 = h - 10/AB
AB = h -10
x = h -10-----------------(2)
Comparing (1) and (2), we get,
h/√3 = h -10
h - h/√3 = 10
h(1 - 1√3) = 10
h(√3 - 1/√3) = 10
h = 10√3/√3 - 1
Taking conjugate,
h = 10√3/√3 - 1 × √3 - 1/√3 - 1
h = 30 + 10√3/3 - 1
h = 30 + 10√3/2
h = 15 + 5√3
h = 5(3 + √3)
h = 5√3 (√3 + 1)
Therefore, the height of the tower is 5√3 (√3 + 1)m.
Q.17. A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h (1 + tan α cot β) meters.
Given, a window of a house is h m above the ground.
From the window, the angle of elevation and depression of the top and bottom of another house situated on the opposite side of the lane are found to be α and β.
We have to prove that the height of the other house is h (1 + tan α cot β) meters.From the figure,
W be the window of the house
Height of the window from the ground, BW = h m
Let OQ be another house.
Height of the another house, QO = Hm
Angle of elevation, ∠QWM = α
Angle of depression, ∠WOB = β
Consider, BO = xm
In triangle QWM,
tan𝛼 = QM/WM
Since, QM = QO - MO,
tanα = H - h/x
x = H - h/tanα -------------(1)
Considering triangle WOB,
tanβ = WB/BO
tanβ = h/x
x = h/tanβ --------------(2)
By comparing (1) and (2), we get,
(H - h)/tan α = h/tan β
(H - h) tan β= h tanα
H tanβ - h tanβ = h tanα
H tanβ = h tanα + h tanβ
H tanβ = h (tanα + tanβ )
H = (h (tanα + tanβ))/tanβ
H = h (tanα /tanβ + 1)
H = h (1 + tanα /tanβ)
H = h (1 + tanα cotβ)
Therefore, the height of the other house is h (1 + tanα cotβ).
Q.18. The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° , respectively. Find the height of the balloon above the ground.
Given, the lower window of a house is at a height of 2 m above the ground
The upper window is 4 m vertically above the lower window.
The angles of elevation of a balloon from these windows are observed to be 60° and 30°
We have to find the height of the balloon above the ground.From the figure,
W₁ be the upper window
W₂ be the lower window
Distance of the lower window from the ground, OR = 2m
Distance of the upper window from the top of the lower window, RQ = 4m
Angle of elevation of balloon from lower window, ∠BW₂R = 60°
Angle of elevation of balloon from upper window, ∠BW₁R = 30°
Height of the balloon from the ground, BO = h m
Distance between the point of observation to the foot, PO = xm
In triangle BW₂R,
tan60° = BR/W₂R
Since, tan60° = √3
√3 = BO - RO/PO
√3 = h - 2/x
x = h - 2/√3 ----------------(1)
In triangle BW₁R,
tan30° = BQ/W₁R
Since, tan30° = 1/√3
1/√3 = h - 6/x
Since, W₁R = PO = x
x = √3(h - 6)--------------(2)
By comparing (1) and (2), we get,
h - 2/√3 = √3(h - 6)
h - 2 = 3(h - 6)
h - 2 = 3h - 18
3h - h = 18 - 2
2h = 16
h = 8m.
Therefore, the height of the balloon above the ground is 8m.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Introduction to Trigonometry - Mathematics (Maths) Class 10
| 1. What is trigonometry? |  |
| 2. How is trigonometry useful in real life? |  |
| 3. What are the three basic trigonometric ratios? |  |
| 4. How can I find the value of trigonometric ratios without a calculator? |  |
| 5. What is the Pythagorean theorem and how is it related to trigonometry? |  |