Quadratic Equations Class 10 Notes Maths Chapter 4
| Table of contents |

|
| What is a Quadratic Equation? |

|
| What is the Root of the quadratic Equation? |

|
| Methods to solve the Quadratic Equations |

|
| 1. Factorisation Method |

|
| 2. Quadratic formula method |

|
What is a Quadratic Equation?
A Quadratic equation is a second-degree polynomial equation that involves the square of a variable. It can have up to two solutions, which may be real or complex.
Standard Form of a Quadratic equation
The standard form of a quadratic equation is written as ax2 +bx + c=0, where a, b, and c are real numbers, and a ≠ 0.

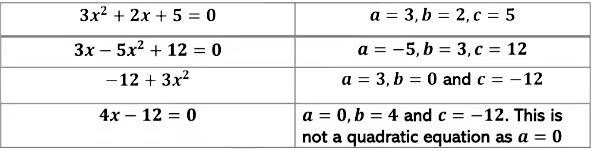
This form is crucial for solving quadratic equations, studying their graphs, and understanding their key properties like roots and symmetry.
Solved Examples
Example 1: Check whether the following are quadratic equations
i) (x + 1)2 = 2(x − 3)
⇒ (x + 1)2 = x2 + 2x + 1
∵ (a + b)2 = a2 + 2ab + b2⇒ x2 + 2x + 1 = 2(x − 3)
⇒ x2 + 2x + 1 = 2x − 6⇒ x2 + 2x + 1 − 2x + 6 = 0
⇒ x2 + 2x − 2x + 6 + 1 = 0
x2 + 7 = 0
The above equation is a quadratic equation, where the coefficient of x is zero, i.e. b = 0
ii) x(x + 1)(x + 8) = (x + 2)(x − 2)
LHS
⇒ x(x + 1)(x + 8)
⇒ x(x2 + 8x + x + 8)⇒ x(x2 + 9x + 8)
⇒ x3 + 9x2 + 8xRHS
(x + 2)(x − 2)
⇒ x2 − 4
∵ (a + b)(a − b) = a2 − b2
Now, x3 + 9x2 + 8x = x2 − 4
⇒ x3 + 9x2 − x2 + 8x + 4 = 0
x3 + 8x2 + 8x + 4 = 0
It is not a quadratic equation as it is an equation of degree 3.
iii) (x − 2)2 + 1 = 2x − 3
LHS
(x − 2)2 + 1 = x2 − 4x + 4 + 1
∵ (a − b)2 = a2 − 2ab + b2
= x2 − 4x + 5
RHS
2x − 3
⇒ x2 − 4x + 5 = 2x − 3
⇒ x2 − 4x − 2x + 5 + 3 = 0
⇒ x2 − 6x + 8 = 0
The above equation is quadratic as it is of the form,
ax2 + bx + c = 0
Example 2: The product of two consecutive positive integers is 420. Form the equation satisfying this scenario.
Let the two consecutive positive integers be x and x + 1
Product of the two consecutive integers= x(x + 1) = 420
⇒ x2 + x = 420
⇒ x2 + x − 420 = 0
x2 + x − 420 = 0, is the required quadratic equation and the two integers satisfy this quadratic equation.
What is the Root of the quadratic Equation?
Let x = α where α is a real number. If α satisfies the Quadratic Equation ax2+ bx + c = 0 such that aα2 + bα + c = 0, then α is the root of the Quadratic Equation.
- As quadratic polynomials have degree 2, therefore, Quadratic Equations can have two roots.
- So the zeros of quadratic polynomial p(x) = ax2 + bx + c are the same as the roots of the Quadratic Equation ax2 + bx + c = 0.
Methods to solve the Quadratic Equations
1. Factorisation Method
In this method, we factorise the equation into two linear factors and equate each factor to zero to find the roots of the given equation.
Step 1: Given Quadratic Equation in the form of ax2 + bx + c = 0.
Step 2: Split the middle term bx as mx + nx so that the sum of m and n is equal to b and the product of m and n is equal to c.
Step 3: By factorisation we get the two linear factors (x + p) and (x + q)
ax2+ bx + c = 0 = (x + p) (x + q) = 0
Step 4: Now we have to equate each factor to zero to find the value of x.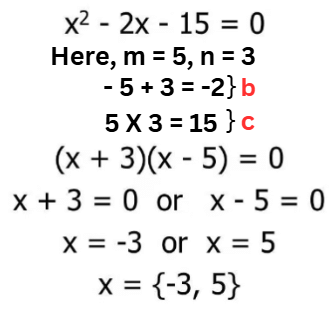
These values of x are the two roots of the given Quadratic Equation.
Solved Examples
Example 1: Solve the following quadratic equation by factorisation method.
i) 4√3x2 + 5x − 2√3 = 0
The given equation is 4√3x2 + 5x − 2√3 = 0
Here, a = 4√3 , b = 5 and c = −2√3
The product of a and c
= 4√3 × (−2√3 )
= −8 × 3
= −24
Factors of 24 = 3 × 8 and 8 + (−3) = 5
The factors of the equation are 8, − 3
So, the given equation can be written as,4√3x2 + (8 − 3)x − 2√3 = 0
⇒ 4 √3x2 + 8x − 3x − 2√3 = 0⇒ 4x( √3x + 2) −√3 (√3 x + 2) = 0
⇒ (4x − √3 )(√3x + 2) = 0
Equating each factor to zero we get,(4x −√3 )=0 and (√3x + 2) = 0
x = and x =
The roots of the equation 4√3x2 + 5x - 2√3 = 0 are: and
ii) 2x2 - 5x + 2 = 0
The given equation is 2x2 - 5x + 2 = 0
Multiplying the above equation by x2 we get,
x2 ( 2x2 - 5x + 2 = 0) ⇒ 2x2x2 - 5x2x + 2x2 = 02 - 5x + 2x2 = 0
Here, a = 2, b = −5 and c = 2
The product of a and c = 2 × 2 = 4
The factors of 4 = 4 × 1 and 4 + 1 = 5
2x2 − (4 + 1)x + 2 = 0
⇒ 2x2 − 4x − 1x + 2 = 0
2x(x − 2) − (x − 2) = 0
(2x − 1)(x − 2) = 0
Equating each factor to zero we get,
(2x − 1) = 0 and (x − 2) = 0
x = 1/2 and x = 2The roots of equation 2x2 − 5x + 2 = 0 are 1/2 and 2
2. Quadratic formula method
In this method, we can find the roots by using a quadratic formula. The quadratic formula is
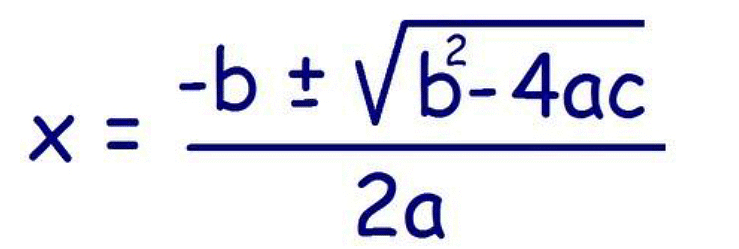
where a, b, and c are the real numbers and b2 – 4ac is called the discriminant.
To find the roots of the equation, put the values of a, b, and c in the quadratic formula.
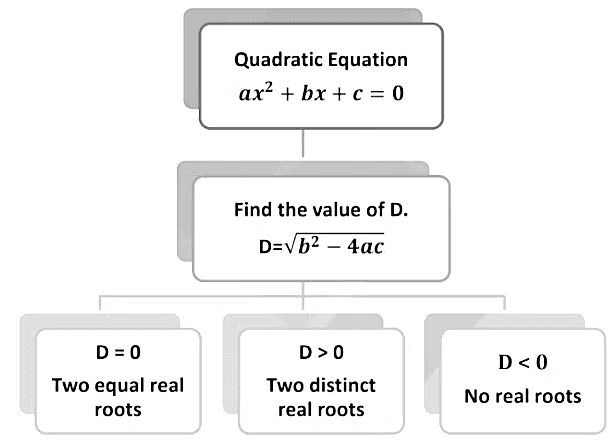
Nature of Roots
From the quadratic formula, we can see that the two roots of the Quadratic Equation are -
x = -b + √(b2 - 4ac)2a and -b - √(b2 - 4ac)2a
or
x = -b ± √D2a
Where D = b2 – 4ac, The nature of the roots of the equation depends upon the value of D, so it is called the discriminant.
Note:
This is called a "discriminant" because it discriminates the roots of the quadratic equation based on its sign.The discriminant is used to find the nature of the roots of a quadratic equation.
- - In this case, the quadratic equation has two distinct real roots.
- - In this case, the quadratic equation has one repeated real root.
- - In this case, the quadratic equation has no real root.
Types of Roots
There are three types of roots of a quadratic equation
ax2 + bx + c = 0
Solved Examples
Example 1: Find the roots of the quadratic equation x2- 7x + 10 = 0 using the quadratic formula.
Solution:
Here, a = 1, b = -7, and c = 10. Then by the quadratic formula:
x = -(-7) ± √((-7)2 - 4(1)(10))2(1)
= 7 ± √(49 - 40)2
= 7 ± √92
= 7 + 32, 7 - 32
= 102, 42
= 5, 2
Therefore, x = 2, x = 5.
Example 2:
Elsie has a two-digit secret number. She gives her friend Mia a few hints to crack it. She says, "It is the value of the discriminant of the quadratic equation
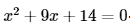

Can you guess the lucky number?
Solution:
The quadratic equation is:
x2 + 9x + 14 = 0
On comparing it with ax2 + bx + c = 0, we get:
a = 1, b = 9, and c = 14
Let's use the discriminant formula to find the discriminant:
Discriminant = b2 - 4ac
= 92- 4(1)(14)
= 81 - 56
= 25
The Lucky Number is 25.
Example 3: The altitude of a right-angled triangle is 7 cm less than its base. If the hypotenuse is 13 cm long, then find the other two sides.
Solution
Let the length of the base be x cm, then altitude = x − 7 cm
Hypotenuse = 13 cm
We know, H2 = P2 + B2
132 = (x − 7)2 + x2
⇒ 169 = x2 − 14x + 49 + x2
⇒ x2 − 14x + 49 + x2 = 169
⇒ 2x2 − 14x + 49 − 169 = 0
⇒ 2x2 − 14x − 120 = 0
Dividing the above equation by 2 we get,x2 − 7x − 60 = 0
Here, a = 1, b = −7 and c = −60
The product of a and c = 1 × (−60) = −60
The factors of 60 = 5 × 12 and −12 + 5 = 7
The given equation can be written as,x2 − 12x + 5x − 60 = 0
x(x − 12) + 5(x − 12) = 0
⇒ (x + 5)(x − 12) = 0
Equating each factor to zero we get,
(x + 5) = 0 and (x − 12) = 0
⇒ x = −5 and x = 12
The length of the base cannot be negative.
Therefore, Base = 12 cm
Altitude = x − 7 cm = 12 − 7 = 5 cm, Hypotenuse = 13 cm
Example 4: Find the roots of the equation,
√5x + 7 = (2x - 7) = 0
Solution:
The given equation is √5x + 7 = (2x - 7) = 0
Squaring both sides of the equation we get,
(√9x + 9)2 = (2x - 7)29x + 9 = 4x2 - 28x + 49
4x2 - 28x + 49 - 9x - 9 = 0
4x2 - 37x + 40 = 0
Here a = 4, b = - 37 and c = 40
Substituting the value of a, b and c in the quadratic formula
x = -b ± √(b2 - 4ac)2a
x = -(-37) ± √(372 - 4×4×40)8
x = 37 ± √7298
Taking the positive root:
x = 37 + 278 = 648 = 8
Taking the negative root:
x = 37 - 278 = 108 = 54
Thus, the solutions are:
x = 8 and x = 54
Example 5: Find the numerical difference of the roots of the equation x2 − 7x − 30 = 0
Solution:
The given quadratic equation is x2 − 7x − 30 = 0
Here a = 1, b = −7 and c = −30
Substituting the value of a, b and c in the quadratic formula
x = -b ± √(b2 - 4ac)2a
Substituting the values:
x = -(-7) ± √(72 - 4 × 1 × (-30))2 × 1
x = 7 ± √(49 + 120)2
x = 7 ± √1692
x = 7 ± 132
Case 1: Taking the positive sign (+):
x = 7 + 132 = 202 = 10
Case 2: Taking the negative sign (-):
x = 7 - 132 = -62 = -3
The two roots are 10 and -3
The difference of the roots= 10 − (−3) = 10 + 3 = 13
Example 6: Find the discriminant of the quadratic equation x2 −4x − 5 = 0
Solution
The given quadratic equation is x2 − 4x − 5 = 0.
On comparing with ax2 + bx + c = 0 we get,
a = 1,b = −4, and c = −5
Discriminant, D = √(b2 - 4ac)
Substituting values:
D = √((-4)2 - 4 × 1 × (-5))
D = √(16 + 20)
D = √36
D = ±6
Example 7: Find the value of p, so that the quadratic equation px(x − 2) + 9 = 0 has equal roots.
Solution
The given quadratic equation is px(x − 2) + 9 = 0
px2 − 2px + 9 = 0Now comparing with ax2 + bx + c = 0 we get,
a = p, b = −2p and c = 9
Discriminant, D = √(b2 - 4ac)D = √((-2p)2 - 4 × p × 9)
D = √(4p2 - 36p)
The given quadratic equation will have equal roots if D = 0
D = √(4p2 - 36p) = 0
4p2 - 36p = 0
4p(p - 9) = 0
p = 0 and p − 9 = 0 ⇒ p = 9
p = 0 and p = 9
The value of p cannot be zero as the coefficient of x, (−2p) will become zero.
Therefore, we take the value of p = 9.
Example 8: If x = −1 is a root of the quadratic equations 2x2 +px + 5 = 0 and the quadratic equation p(x2 + x) + k = 0 has equal roots, then find the value of k.
Solution:
The given quadratic equation is 2x2 + px + 5 = 0. If x = −1 is the root of the equation then,
2(−1)2 + p(−1) + 5 = 0
2 − p + 5 = 0
⇒ −p = −7
p = 7
Putting the value of p in the equation p(x2 + x) + k = 0,
7(x2 + x) + k = 0
⇒ 7x2 + 7x + k = 0
Now comparing with ax2 + bx + c = 0 we get,
a = 7, b = 7 and c = kDiscriminant, D = √(b2 - 4ac)
D = √((7)2 - 4 × 7 × k)
D = √(49 - 28k)
The given quadratic equation will have equal roots if D = 0
D = √(49 - 28k) = 0
49 - 28k = 0
28k = 49
k = 4928 = 74
Therefore, the value of k is 7/4.
|
127 videos|584 docs|79 tests
|
FAQs on Quadratic Equations Class 10 Notes Maths Chapter 4
| 1. What is a quadratic equation? |  |
| 2. What are the roots of a quadratic equation? |  |
| 3. What is the factorization method for solving quadratic equations? |  |
| 4. How do you apply the quadratic formula to solve a quadratic equation? |  |
| 5. What is the significance of the discriminant in a quadratic equation? |  |
















