Class 10 Maths Chapter 2 HOTS Questions - Polynomials
Q1: Find the Quadratic polynomial whose sum and product of zeros are √2 + 1, 1/√2 + 1 .
Ans: sum = 2 √2
Product = 1
Q.P = X2 – (sum) x + Product
∴ x2 – (2 √2 ) x + 1
Q2: If α,b are the zeros of the polynomial 2x2 – 4x + 5 find the value of a) α2 + β2 b) (α - β)2.
Ans: p (x) = 2 x2 – 4 x + 5
α + β = -b/a = 4/2 = 2
αβ = c/a = 5/2
α2 + β2 = (α + β)2 – 2αβ
Substitute then we get, α 2 + β2 = -1
(α - β)2 = (α + β)2 - 4 α β
Substitute, we get = (α - β)2 = - 6
Q3: If the squared difference of the zeros of the quadratic polynomial x2 + px + 45 is equal to 144 , find the value of p.
Ans: Let two zeros are a and b where α > β
According given condition
(α - β)2 = 144
Let p(x) = x2 + px + 45
α + β = -b/a = -p/1 = -p
αβ = c/a = 45/1 = 45
now (a - β)2 = 144
(α + β)2 – 4 αβ = 144
(-p)2 – 4 (45) = 144
Solving this we get p = ± 18
Q4: If α, β are the zeros of a Quadratic polynomial such that α + β = 24, α - β = 8. Find a Quadratic polynomial having α and β as its zeros.
Ans: α + β = 24
α - β = 8
_________
2α = 32
α = 32/2 = 16, ∴ α = 16
Work the same way to α+β = 24
So, β = 8
Q.P is x2 – (sum) x + product
= x2 – (16+8) x + 16 x 8
Solve this,
it is k (x2 – 24x + 128)
Q5: If α and β are the zeroes of the polynomial x2 + 8x + 6 frame a quadratic polynomial whose zeroes are
(a) 1/α and 1/β
(b) 1 + β/α, 1 + α/β.
Ans: Given polynomial x2 + 8x + 6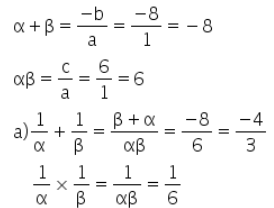
Hence, the Required Quadratic polynomial f(x) is given by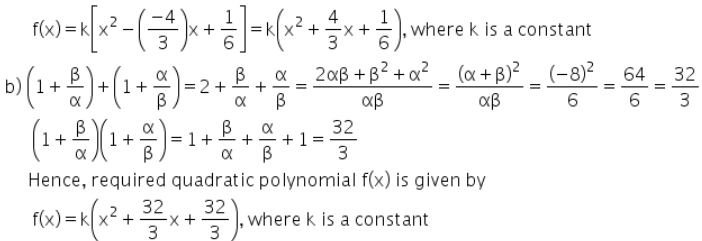
Q6: If α & β are the zeroes of the polynomial 2x2 - 4x + 5, then find the value of
(i) α2 + β2
(ii) 1/a + 1/ß
(iii) (α - β)2
(iv) 1/α2 + 1/β2
(v) α3 + β3
Ans: 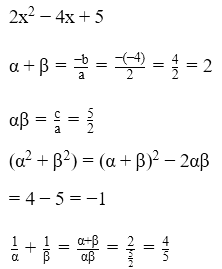
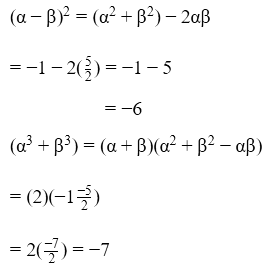
Q7: If the ratios of the polynomial ax3 + 3bx2 + 3cx + d are in AP, Prove that 2b3 - 3abc + a2d = 0
Ans: Let the zeros of the given polynomial be p, q, r. As the roots are in A.P., then it can be assumed as p−k, p, p + k, where k is a common difference.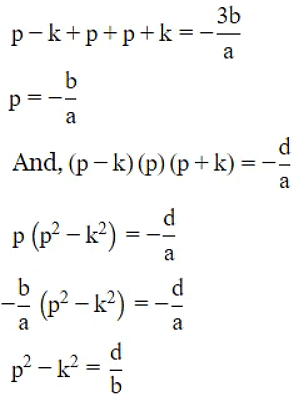
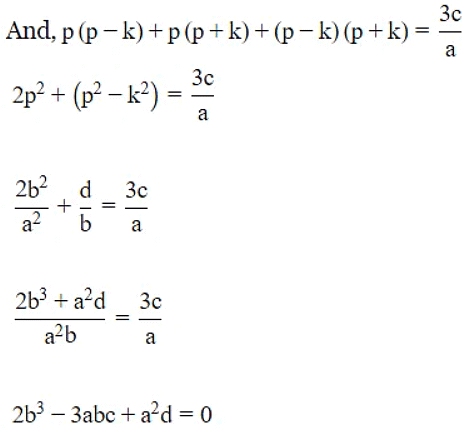
Q8: If α and β are the zeros of a quadratic polynomial such that α+β=15 and α−β=9, find the quadratic polynomial having α and β as its zeros.
Ans: Given:
α+β=15
α−β=9
From α+β=15:
2α = 15+9 = 24 ⇒ α=12
From α−β=9:
2β = 15−9 = 6 ⇒β=3
Quadratic polynomial:
p(x) = x2− (α+β)x +αβ
Substitute:
p(x)=x2−15x+36
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 2 HOTS Questions - Polynomials
| 1. What is a polynomial and how is it different from other algebraic expressions? |  |
| 2. How do you classify polynomials based on their degree and number of terms? |  |
| 3. What are the different methods to factor polynomials? |  |
| 4. Can you explain the Remainder Theorem and how it is applied to polynomials? |  |
| 5. What role do polynomials play in solving real-world problems? |  |

















