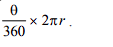Area Related to Circles Class 10 Notes Maths Chapter 11
| Table of contents |

|
| Introduction |

|
| Area of a Sector of a Circle |

|
| Area of Segment of a circle |

|
| Solved Examples |

|
Introduction
- A circle can be split into parts called sectors and segments, which are important for understanding areas related to circles.
- A sector is the space between two radii and the arc they create, while a segment is the area found between a chord and the arc.
- Note: When we mention 'segment' and 'sector', we refer to the minor segment and minor sector unless specified otherwise.
- This chapter presents formulas to find the area of a sector, the length of an arc, and the area of a segment, which assist in solving practical problems related to these areas. The area of a segment is calculated as follows: Area of segment. Area of the corresponding sector. Area of the corresponding triangle.
- Additionally, the distinction between minor and major sectors and segments is highlighted for clarity.
Sector of Circle
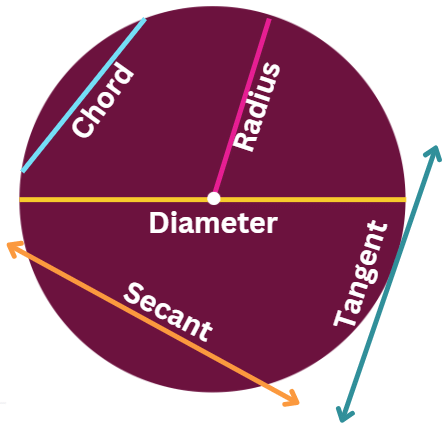
The area of a circular region that is bounded by two radii and the arc between them is known as a sector of the circle.
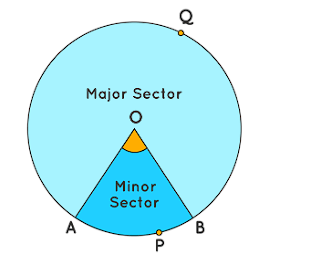
- The portion OAPB of the circle is called the minor sector and the portion OAQB of the circle is called the major sector.
- ∠ AOB is called the angle of the sector.
- The angle of the major sector can be calculated as 360° minus the angle of the minor sector.
Arc
An arc is a portion of the circle's circumference.
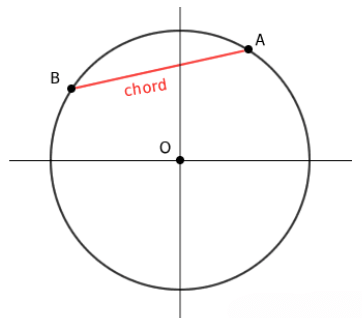
Chord
A chord is a line segment that joins any two points on the circle's circumference.
Segment of Circle
The area of a circular region that lies between a chord and the corresponding arc is referred to as a segment of the circle.
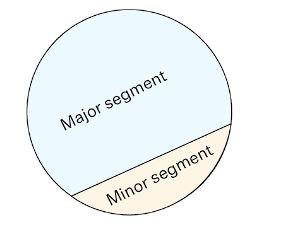
- A minor segment is made by a minor arc.
- A Major segment is made by a major arc of the circle.
Remark: When we mention 'segment' or 'sector', we are referring to the 'minor segment' and the 'minor sector' respectively, unless indicated otherwise.
Area of a Sector of a Circle
Sector: Sector of a Circle is given as part of a Circle enclosed by 2 radii and an arc.
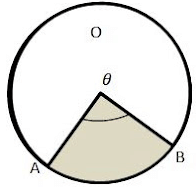
In the diagram, the shaded area OAB is the sector.
Here, θ is the angle subtended by the arc AB on the center O of the circle.
The area of the Sector is given as 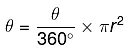
In the whole circle, the angle θ will be 360°
Area of Circle = πr2
Using Unitary Method
Area represented by 360° = πr2
Area represented by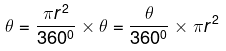
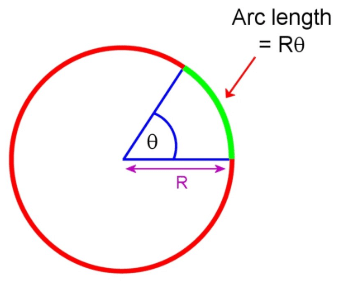
Length of an Arc of a sector of angle θ =
Solved Examples
Q1: Calculate the area of a sector with a radius of 20 yards and an angle of 90 degrees.
Ans: 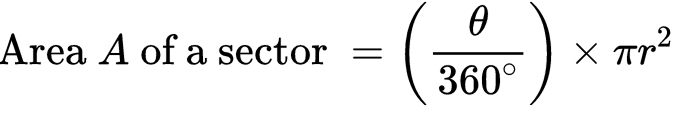 here θ = 90º,
here θ = 90º,
r = 20 yards,
π = 3.141
= (90º/360º) X 3.141 X (20)2
= (1256.4/4) yards2
= 314.1 yards2
Q2: Calculate the area of a sector of angle 60°. Given, the circle has a radius of 6 cm.
Ans:  The angle of the sector = 60°
The angle of the sector = 60°
Using the formula,
The area of the sector = (θ/360°) × π r²
= (60/360) × π r² cm²
Or, area of the sector = 6 × 22/7 cm² = 132/7 cm²
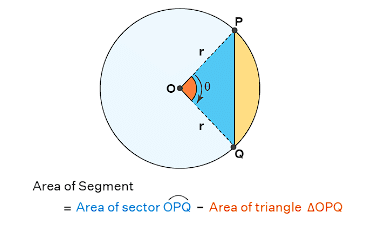
Area of Segment of a circle
In the diagram Shaded portion represents Segment AMB
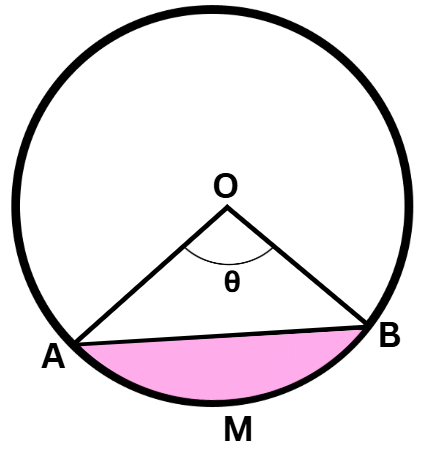
Area of Segment AMB = Area of Sector OAB- Area of triangle AOB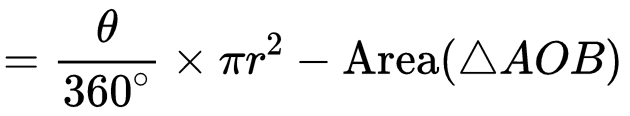

Solved Examples
Q1: A chord subtends an angle of 90°at the centre of a circle whose radius is 20 cm. Compute the area of the corresponding major segment of the circle..
Ans: Area of the sector = θ/360 × π × r²
Base and height of the triangle formed will be = radius of the circle
Area of the minor segment = area of the sector – area of the triangle formed
Area of the major segment = area of the circle – area of the minor segment
Now,
Radius of circle = r = 20 cm and
Angle subtended = θ = 90°
Area of the sector = θ/360 × π × r² = 90/360 × 22/7 × 20²
Or, area of the sector = 314.2 cm²
Area of the triangle = ½ × base × height = ½ × 20 × 20 = 200 cm²
Area of the minor segment = 314.2 – 200 = 114.2 cm²
Area of the circle = π × r² = (22/7) × 20² = 1257.14
Area of the major segment = 1257.14 – 114.2 = 1142.94 cm²
So, the area of the corresponding major segment of the circle = 1142.94 cm²
Q2: Find the area of the segment AYB shown in the figure, if the radius of the circle is 21 cm and ∠ AOB = 120°. (Use π = 22/7).
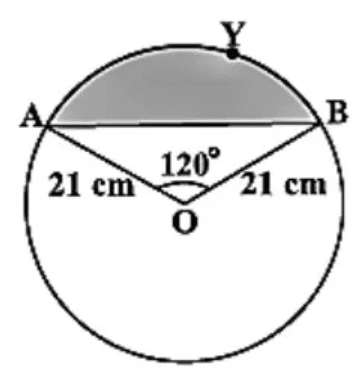
Ans: Area of the segment AYB = Area of sector OAYB – Area of Δ OAB …..(1)
Area of the sector OAYB = (120/360) × (22/7) × 21 × 21 = 462 cm² ……(2)
Draw OM ⊥ AB.
OA = OB (radius)
Therefore, by RHS congruence, Δ AMO ≅ Δ BMO.
M is the mid-point of AB and ∠ AOM = ∠ BOM = (1/2) × 120° = 60°
Let OM = x cm
In triangle OMA,
OM/OA = cos 60°
x/21 = ½
x = 21/2
OM = 21/2 cm
Similarly,
AM/OA = sin 60°
AM/21 = √3/2
AM = 21√3/2 cm
AB = 2 × AM = 2 (21√3/2) = 21√3 cm
Area of triangle OAB = (½) × AB × OM
= (½) × 21√3 × (21/2)
= (441/4)√3 cm² …(3)
From (1), (2), and (3),
Area of the segment AYB = [462 – (441/4)√3] cm²
|
127 videos|655 docs|84 tests
|
FAQs on Area Related to Circles Class 10 Notes Maths Chapter 11
| 1. What is the formula for calculating the area of a sector of a circle? |  |
| 2. How do you find the area of a segment of a circle? |  |
| 3. Can you explain the difference between the area of a sector and the area of a segment? |  |
| 4. What is the significance of the angle in the calculations for a sector's area? |  |
| 5. How can I apply the concepts of area related to circles in real-life situations? |  |