Wheatstone Bridge & Meter Bridge | Physics Class 12 - NEET PDF Download
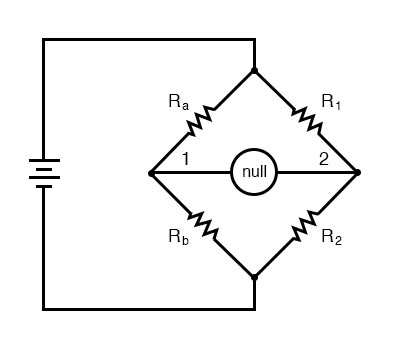
(i) Wheatstone designed a network of four resistances with the help of which the resistance of a given conductor can be measured. Such a network of resistances is known as Wheastone's bridge.
(ii) In this bridge, four resistance P, Q, R and S are so connected so as to form a quadrilateral ABCD. A sensitive galvanometer and key K2 are connected between diagonally opposite corners B and D, and a cell and key K1 are connected between two other corners A and C (figure shown)
(iii) When key K1 is pressed, a current i flows from the cell. On reaching the junction A, the current i gets divided into two parts i1 and i2. Current i1 flows in the arm AB while i2 in arm AD. Current i1, on reaching the junction B gets further divided into two parts (i1 - ig) and ig, along branches BC and BD respectively. At junction D, currents i2 and ig are added to give a current (i2 ig), along branch DC. (i2 - ig) and (i2 ig) add up at junction C to give a current (i1 i2) or i along branch CE. In this way, currents are distributed in the different branches of bridge. In this position, we get a deflection in the galvanometer.
(iv) Now the resistance P,Q,R and S are so adjusted that on pressing the key K2, deflection in the galvanometer becomes zero or current ig in the branch BD becomes zero. In this situation, the bridge is said to be balanced.
(v) In this balanced position of bridge, same current i1 flows in arms AB and BC and similarly same current i2 in arms AD and DC. In other words, resistances P and Q and similarly R and S, will now be joined in series.
(vi) Condition of balance : Applying Kirchhoff's 2nd law to mesh ABDA, i1P + igG - i2R = 0 ...(1)
Similarly, for the closed mesh BCDB, we get, (i1 - ig) Q - (i2 + ig)S - igG = 0 ...(2) When bridge is balanced, ig = 0. Hence eq. (1) & (2) reduce to
i1P - i2R = 0 or i1P = i2R ....(3)
i1Q - i2S = 0 or i1Q = i2S ...(4)
Dividing (3) by (4), we have,  ....(5)
....(5)
This is called as condition of balanced for Wheatstone's Bridge.
(vii) It is clear from above equation that if ratio of the resistance P and Q, and the resistance R are known, then unknown resistance S can be determined. This is the reason that arms P and Q are called as ratio arms, arm AD as known arm and arm CD as unknown arm.
(viii) When the bridge is balanced then on inter-changing the positions of the galvanometer and the cell there is no effect on the balance of the bridge. Hence the arms BD and AC are called as conjugate arms of the bridge.
(ix) The sensitivity of the bridge depends upon the value of the resistances. The sensitivity of bridge is maximum when all the four resistances are of the same order.
Ex.22 Find equivalent resistance of the circuit between the terminals A and B.

Sol. Since the given circuit is wheat stone bridge and it is in balance condition.
Because, 10 × 3 =30 = 6× 5
hence this is equivalent to


Ex.23 Find the equivalent resistance between A and B

Sol. This arrangement can be modified as shown in figure since it is balanced wheat stone bridge.


8.1 Unbalanced Wheatstone Bridge
Ex.24

Find equivalent resistance ?
Sol. Let potential at point B is x and E is Y

Applying KCl at point B

8x - 5y = v ...(1)
Applying KCL at point E

⇒ 8y - 5x = 2v ...(2)
solving x & y  ,
, 
current from branches BC & EF adds up to give total current (i) flowing in the circuit.
i = i3 i4 =  =
= 
Because,  Therefore, Req. =
Therefore, Req. = 
Ladder Problem :

Find the effective resistance between A & B ?
Sol. Let the effective resistance between A & B be RE since the network is infinite long, removal of one cell from the chain will not change the network. The effective resistance between points C & D would also be RE.
The equivalent network will be as shown below

The original infinite chain is equivalent to R in series with R & RE in parallel.

RER + RE2 = R2 + 2RRE ⇒ RE2 - RRE - R2 = 0

Ex.25

Find the equivalent resistance between A & B ?
Sol. As moving from one section to next one, resistance is increasing by k times. Since the network is infinitely long, removal of one section from the chain will bring a little change in the network. The effective resistance between points C & D would be kRE (where RE is the effective resistance)
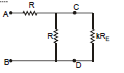
Therefore, Effective R between A & B.

On solving we get

15. Symmetrical Circuits :
Some circuits can be modified to have simpler solution by using symmetry if they are solved by traditional method of KVL and KCL then it would take much time.
Ex.26 Find the equivalent Resistance between A and B

Sol. I Method : mirror symmetry
The branches AC and AD are symmetrical
Therefore, current through them will be same.
The circuit is also similar from left side and right side like mirror images with a mirror placed alone CD therefore current distribution while entering through B and an exiting from A will be same. Using all these facts the currents are as shown in the figure. It is clear that current in resistor between C and E is 0 and also in ED is 0. It's equivalent is shown in figure (b)



II Method : folding symmetry
Therefore, The potential difference in R between (B, C) and between (B, D) is same VC = VD
Hence the point C and D are same hence circuit can be simplified as

This is called folding.
Now , it is Balanced Wheatstone bridge


 In II Method it is not necessary to know the currents in CA and DA
In II Method it is not necessary to know the currents in CA and DA
Ex.27 Find the equivalent Resistance between A and B

Sol. In this case the circuit has symmetry in the two branches AC and AD at the input
Therefore, current in them are same but from input and from exit the circuit is not similar
(Because, on left R and on right 2R)
Therefore, on both sides the distribution of current will not be similar.
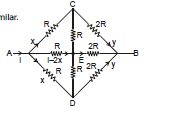
Here Vc = Vd
hence C and D are same point
So, the circuit can be simplified as
Now it is balanced wheat stone bridge.

 =
= 
Ex.28 Find the equivalent Resistance between A and B

Sol. 
Here VA = VC and VB = VD
Here the circuit can be simplified as

 =
= 
Ans. 


Ex.29 Twelve equal resistors each R W are connected to form the edges of a cube. Find the equivalent resistances of the network.
(a) When current enters at 1 & leaves at 6 (body diagonal)
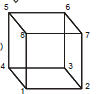
Sol. Here 2, 4, 8 are equipotential points (if we move from 1 → 2, 4, 8 it comes along the edge & 6 → 2, 4, 8 it comes along face diagonal). Similarly 3, 5, 7 are equipotential points.


(b) When current enters at 1 and leaves at 2
Sol. Here 3, 7 are equipotential surface (if we move from 1 → 3, 7 we have along face and 2, →3, 7 we move along edge) similarly 4, 8 are equipotential surface.


(c) When current enters at 1 and leaves at 3
Sol. If we cut the cube along the plane passing through 2, 4, 5, 7 then by mirror symmetry, the final configuration will be



Meter Bridge
It is based on principle of whetstone bridge. It is used to find out unknown resistance of wire. AC is 1 m long uniform wire R.B. is known resistance and S is unknown resistance. A cell is connected across 1 m long wire and Galvanometer is connected between Jockey and midpoint D. To find out unknown resistance we touch jockey from A to C and find balance condition. Let balance is at B point on wire.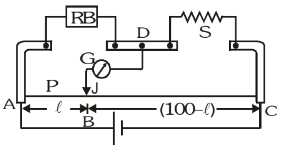
AB = ℓ cm P = r ℓ
BC = (100 – ℓ) cm Q = r(100 – ℓ) where r = resistance per unit length on wire.
At balance condition :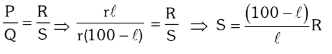
|
97 videos|336 docs|104 tests
|
FAQs on Wheatstone Bridge & Meter Bridge - Physics Class 12 - NEET
| 1. What is a Wheatstone bridge and how does it work? |  |
| 2. How can a Wheatstone bridge be used to measure an unknown resistance? |  |
| 3. What is a meter bridge and what is its purpose? |  |
| 4. How does a meter bridge work? |  |
| 5. How accurate are the measurements obtained using a meter bridge? |  |

|
Explore Courses for NEET exam
|

|


















