Class 10 Maths Chapter 8 Practice Question Answers - Introduction to Trigonometry
Q1. If sec θ + tan θ = 7, then evaluate sec θ – tan θ.
View Answer 
Sol:
We know that,
sec2θ – tan2θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
⇒ (7) (sec θ – tan θ) = 1 …[sec θ + tan θ = 7]
∴ sec θ – tan θ = 1/7
Q2. Prove that
(1+tan A - sec A) (1+tan A + sec A) = 2 tan A
View Answer Sol:
LHS = (1+tan A)2 - sec2 A
= 1+ tan2 A + 2 tan A - sec2 A
= sec2 A + 2 tan A - sec2 A
= 2 tan A = RHS
Q3. If tan A = cot B, then find the value of (A+B)
View Answer Sol:
We have,
tan A = cot B
tan A = tan(90°-B)
A = 90° - B
Thus, A + B = 90°
Q4. If sinθ + sin2θ = 1 then prove that cos2θ + cos4θ = 1.
View Answer Sol:
sinθ + sin2θ = 1
⇒ sinθ + (1-cos2θ) = 1
⇒ sinθ - cos2θ = 0
⇒ sinθ = cos2θ
Squaring both sides, we get
sin2θ = cos4θ
⇒ 1 - cos2θ = cos4θ
⇒ cos4θ + cos2θ = 1
Q5. If tan θ + cot θ = 5, find the value of tan2θ + cotθ.
View Answer Sol:
tan θ + cot θ = 5 …[Given]
⇒ tan2θ + cot2θ + 2 tan θ cot θ = 25 …[Squaring both sides]
⇒ tan2θ + cot2θ + 2 = 25
∴ tan2θ + cot2θ = 23
Q6. If sec 2A = cosec (A – 27°) where 2A is an acute angle, find the measure of ∠A.
View Answer Sol:
sec 2A = cosec (A – 27°)
⇒ cosec(90° – 2A) = cosec(A – 27°) …[∵ sec θ = cosec (90° – θ)]
⇒ 90° – 2A = A – 27°
⇒ 90° + 27° = 2A + A
⇒ 3A = 117°
∴ ∠A = 117°/3 = 39°
Q7. Evaluate: sin2 19° + sin271°.
View Answer Sol:
sin219° + sin271°
= sin219° + sin2 (90° – 19°) …[∵ sin(90° – θ) = cos θ]
= sin2 19° + cos2 19° = 1 …[∵ sin2 θ + cos2 θ = 1]
Q8. In a triangle ABC, write cos(B+C/2) in terms of angle A.
View Answer Sol:
In a triangle,
A+B+C = 180°
B+C = 180° - A
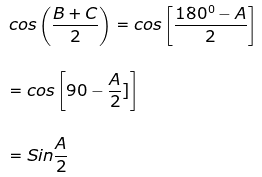
Q9. If secθ sinθ = 0, then find the value of θ.
View Answer Sol:
We have,
secθ sinθ = 0
Thus θ = 0
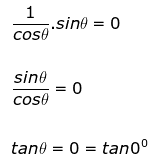
Q10. Find the value of sin241° + sin249°
View Answer Sol:
sin241° + sin249°
= sin2(90°-49°) + sin249°
= cos249° + sin249°
= 1
Q11. If tan A = cot B, prove that A + B = 90°.
View Answer Sol:
tan A = cot B
∴ tan A = tan (90° − B)
⇒ A = 90° − B
⇒ A + B = 90°
Q12. Express sin 67° + cos 75° in terms of ratios of angles between 0° and 45°.
Sol:
View Answer ∵ 67° = 90° − 23° and 75° = 90° − 15°
∴ sin 67° + cos 75°
= sin (90° − 23°) + cos (90° − 15°)
= cos 23° + sin 15°
Q13. What is the value of sinθ. cos(90° - θ) + cosθ . sin(90° - θ)?
View Answer Sol:
sinθ ·cos(90° − θ) + cosθ · sin(90° − θ)
= sinθ · sinθ + cosθ · cosθ [∵ cos(90° − θ) = sinθ , sin(90° − θ) = cos θ]
= sin2 θ + cos2 θ = 1
Q14. If tan θ = cot (30° + θ ), find the value of θ .
View Answer Sol:
We have,
tan θ = cot (30° + θ)
= tan [90° − (30° + θ)]
= tan [90° − 30° − θ]
= tan (60° − θ)
⇒ θ = 60° − θ
⇒ θ + θ = 60°
⇒ 2θ = 60°
⇒ θ = 60°/2
⇒ θ = 30°
Q15. If sin 3θ = cos (θ - 6)° and 3θ and (θ - 6)° are acute angles, find the value of θ.
View Answer Sol:
We have,
sin3θ = cos(θ − 6)° = sin[90°−(θ − 6)°] ∵ [sin (90° − θ) = cos θ]
⇒ 3θ = 90° − (θ − 6)°
⇒ 3θ = 90° − θ + 6°
⇒ 3θ + θ = 96°
⇒ 4θ = 96°/4
⇒ θ = 24°
Q16. Show that: tan 10° tan 15° tan 75° tan 80° = 1
View Answer Sol:
We have,
L.H.S. = tan 10° tan 15° tan 75° tan 80°
= tan (90° − 80°) tan 15° tan (90° − 15°) tan 80°
= cot 80° tan 15 cot 15° tan 80°
= (cot 80° × tan 80°) × (tan 15° × cot 15°)
= 1× 1
= 1 = R.H.S.
Introduction to Trigonometry Class 10 Maths Important Questions Short Answer-I (2 Marks)
17. If tan 2A = cot (A - 18°), where 2A is an acute angle, find the value of A.
Sol:
tan 2A = cot (A - 18°)
⇒ cot (90° - 2A) = cot (A - 18°) [∵ cot (90° -0) - tan θ]
⇒ 90° - 2A = A - 18°
⇒ 3A = 108°
⇒ A = 108°/3
⇒ A = 36°
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 8 Practice Question Answers - Introduction to Trigonometry
| 1. What is the definition of trigonometry and its importance in mathematics? |  |
| 2. What are the primary trigonometric functions, and how are they defined in relation to a right triangle? | |
| 3. How do the unit circle and the right triangle relate to trigonometric functions? | |
| 4. What are the inverse trigonometric functions, and why are they useful? | |
| 5. How do trigonometric identities facilitate the simplification of expressions in trigonometry? | |
Extra Questions
,Viva Questions
,study material
,ppt
,mock tests for examination
,Class 10 Maths Chapter 8 Practice Question Answers - Introduction to Trigonometry
,video lectures
,Important questions
,Summary
,past year papers
,Free
,Class 10 Maths Chapter 8 Practice Question Answers - Introduction to Trigonometry
,MCQs
,Exam
,Previous Year Questions with Solutions
,Class 10 Maths Chapter 8 Practice Question Answers - Introduction to Trigonometry
,Sample Paper
,practice quizzes
,Objective type Questions
,Semester Notes
,shortcuts and tricks
;
Practice Questions: Introduction to Trigonometry Free PDF Download
Importance of Practice Questions: Introduction to Trigonometry
Practice Questions: Introduction to Trigonometry Notes
Practice Questions: Introduction to Trigonometry Class 10
Study Practice Questions: Introduction to Trigonometry on the App
|
© EduRev
|
Education Revolution
|
|
