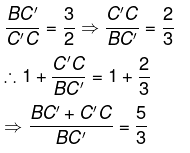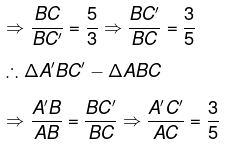Constructions Class 10 Notes Maths
Introduction
In Class IX, we learned how to create geometric shapes using a ruler and compass, like angle bisectors and perpendicular bisectors. Now, we're going to explore more constructions, building on what we already know. This time, we'll focus on understanding the math behind each construction.
Division of a Line Segment
Construction 1: To divide a line segment in a given ratio.
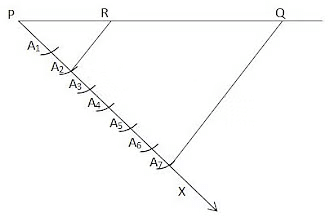
Q: Draw Line segment PQ=9cm and divide it in the ratio 2:5. Justify your construction.
Sol:
Steps of construction:
(i) Draw Line Segment PQ=9cm
(ii) Draw a Ray PX, making an acute angle with PQ.
(iii) Mark 7 points A1 , A2 , A3 …A7 along PX such that PA1 = A3A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7
(iv) Join QA7
(v) Through the point A2 , draw a line parallel to A7Q by making an angle equal to ∠PA7Q at A2, intersecting PQ at point R. PR:RQ = 2:5Justification:
We have A2R || A7Q
Construction 2: To construct a triangle similar to a given triangle as per the given scale factor.
Scale Factor means the ratio of the sides of the triangle to be constructed with the corresponding sides of the given triangle.
This construction involves two cases:(i) Where the new triangle is smaller than the given triangle.
(ii) Where the new triangle is larger than the given triangle.
Case 1: When the scale factor is greater than 1.
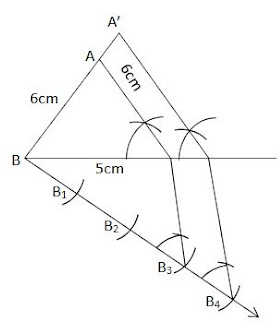
Q: Construct an isosceles triangle with a base of 5 cm and equal sides of 6 cm. Then, construct another triangle whose sides are of the corresponding sides of the (4/3)th of the first triangle.
Sol:
Steps of construction:
(i) Draw BC = 5 cm
(ii) With B and C as the centre and radius 6 cm, draw arcs on the same side of BC, intersecting at A.
(iii) Join AB and AC to get the required ΔABC.
(iv) Draw a ray , making an acute angle with BC on the side opposite to the vertex A.
(v) Mark 4 points B1, B2, B3, B4, along BX such that BB1 = B1B2 = B2B3 = B3B4
(vi) Join B3C. Draw a line through B4 parallel to B3C, making an angle equal to ∠BB3C intersecting the extended line segment BC at C´.
(vii) Through point C´, draw a line parallel to CA, intersecting extended BA at A´.
(viii) The resulting ΔA´BC´ is the required triangle.
Case 2: When the scale factor is less than 1.
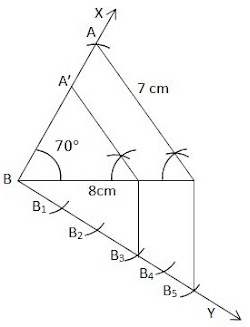
Q: Draw a ΔABC with sides BC = 8 cm, AC = 7 cm, and ÐB = 70°. Then, construct a similar triangle whose sides are (3/5)th of the corresponding sides of the ΔABC.
Sol:
Steps of construction:
(i) Draw BC = 8 cm
(ii) At B, draw ∠XBC = 70°
(iii) With C as centre and radius 7 cm, draw an arc intersecting BX at A.
(iv) Join AB, and DABC is thus obtained.
(v) Draw a ray , making an acute angle with BC.
(vi) Mark 5 points, B1, B2, B3, B4, B5, along BY such that
(vii) BB1 = B1B2 = B2B3 = B3B4 = B4B5
(viii) Join CB5
(ix) Through the point B3, draw a line parallel to B5C by making an angle equal to ∠BB5C, intersecting BC at C´.
(x) Through the point C´, draw a line parallel to AC, intersecting BA at A´. Thus, ΔA´BC´ is Required Triangle.Justification
Using BPT
Construction of tangents to a circle
We know that a point inside a circle has no tangent. On the circle, there's a unique tangent perpendicular to the radius at that point. Extend the radius and draw a line perpendicular to it to create the tangent. For a point outside the circle, two tangents can be drawn. We'll now see how to construct these tangents.
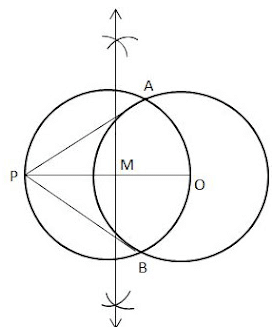
Construction: To construct tangents to a circle from a point outside it.
Q: Draw a circle of radius 3 cm. From a point 5 cm away from its center, construct a pair of tangents to the circle and measure their lengths.
Sol:
Steps of construction:
(i) Draw a circle with centre O and radius 3 cm. Take a point P such that OP = 5 cm, and then join OP.
(ii) Draw the perpendicular bisector of OP. Let M be the mid point of OP.
(iii) With M as the centre and OM as the radius, draw a circle. Let it intersect the previously drawn circle at A and B.
(iv) Joint PA and PB. Therefore, PA and PB are the required tangents. It can be observed that PA=PB=4cm.
FAQs on Constructions Class 10 Notes Maths
| 1. What is the concept of division of a line segment? |  |
| 2. How can tangents to a circle be constructed? |  |
| 3. How is the division of a line segment related to similar triangles? |  |
| 4. What is the significance of constructing tangents to a circle? |  |
| 5. Can a line segment be divided into two unequal parts? |  |